This is the multi-page printable view of this section. Click here to print.

Return to the regular view of this page.

Documentation

This section is where the HEIR documentation lives.

1 - Getting Started

Getting HEIR

Using a pre-built nightly binary

HEIR releases a nightly binary for Linux x86-64. This is intended for testing compiler passes and not for production use.

wget https://github.com/google/heir/releases/download/nightly/heir-opt
chmod +x heir-opt
./heir-opt --help

Then you can run the examples below, replacing bazel run //tools:heir-opt -- with ./heir-opt. HEIR also publishes heir-translate and heir-lsp in the same way.

Via pip

We publish a python package heir_py that includes the heir-opt and heir-translate binaries.

python -m venv venv
source venv/bin/activate

pip install heir_py

heir-opt --help
heir-translate --help

Building From Source

Prerequisites

  • Git
  • A C++ compiler and linker (clang and lld or a recent version of gcc). If you want to run OpenFHE with parallelism (enabled by default), you’ll also need OpenMP.
  • Bazel via bazelisk. The precise Bazel version used is in .bazelversion in the repository root.
Detailed Instructions The first two requirements are frequently pre-installed or can be installed via the system package manager. For example, on Ubuntu, these can be installed with
sudo apt-get update && sudo apt-get install clang lld libomp-dev

You can download the latest Bazelisk release, e.g., for linux-amd64 (see the Bazelisk Release Page for a list of available binaries):

wget -c https://github.com/bazelbuild/bazelisk/releases/latest/download/bazelisk-linux-amd64
mv bazelisk-linux-amd64 bazel
chmod +x bazel

You will then likely want to move bazel to a location on your PATH, or add its location to your PATH, e.g.:

mkdir -p ~/bin
echo 'export PATH=$PATH:~/bin' >> ~/.bashrc
mv bazel ~/bin/bazel

Note that on linux systems, your OS user must not be root as bazel might refuse to work if run as root.

On macOS, you can install bazelisk via Homebrew.

Clone and build the project

You can clone and build HEIR from the terminal as described below. Please see Development for information on IDE configuration if you want to use an IDE to build HEIR.

git clone git@github.com:google/heir.git && cd heir
bazel build @heir//tools:heir-opt

Some HEIR passes require Yosys as a dependency (--yosys-optimizer), which itself adds many transitive dependencies that may not build properly on all systems. If you would like to skip Yosys and ABC compilation, use the following build setting:

bazel build --//:enable_yosys=0 --build_tag_filters=-yosys @heir//tools:heir-opt

Adding the following to .bazelrc in the HEIR project root will make this the default behavior

common --//:enable_yosys=0
common --build_tag_filters=-yosys

Optional: Run the tests

bazel test @heir//...

Using HEIR

Run the dot-product example

The dot-product program computes the dot product of two length-8 vectors of 16-bit integers (i16 in MLIR parlance). This example will showcase the OpenFHE backend by manually calling the relevant compiler passes and setting up a C++ harness to call into the HEIR-generated functions.

The input program is in tests/Examples/common/dot_product_8.mlir. Support for standard input languages like C and C++ are currently experimental at best, but eventually we would use an MLIR-based tool to convert an input language to MLIR like in that file. The program is below:

func.func @dot_product(%arg0: tensor<8xi16> {secret.secret}, %arg1: tensor<8xi16> {secret.secret}) -> i16 {
  %c0 = arith.constant 0 : index
  %c0_si16 = arith.constant 0 : i16
  %0 = affine.for %arg2 = 0 to 8 iter_args(%iter = %c0_si16) -> (i16) {
    %1 = tensor.extract %arg0[%arg2] : tensor<8xi16>
    %2 = tensor.extract %arg1[%arg2] : tensor<8xi16>
    %3 = arith.muli %1, %2 : i16
    %4 = arith.addi %iter, %3 : i16
    affine.yield %4 : i16
  }
  return %0 : i16
}

For an introduction to MLIR syntax, see the official docs or this blog post.

Now we run the heir-opt command to optimize and compile the program. If you fetched a pre-built binary instead of building from source, then all commands below should have bazel run //tools:heir-opt -- replaced with heir-opt, and similarly for heir-translate.

bazel run //tools:heir-opt -- \
--mlir-to-bgv='ciphertext-degree=8'\
--scheme-to-openfhe='entry-function=dot_product'  \
$PWD/tests/Examples/common/dot_product_8.mlir > output.mlir

This produces a file in the openfhe exit dialect (part of HEIR).

!Z1005037682689_i64_ = !mod_arith.int<1005037682689 : i64>
!Z1032955396097_i64_ = !mod_arith.int<1032955396097 : i64>
!Z1095233372161_i64_ = !mod_arith.int<1095233372161 : i64>
#polynomial_evaluation_encoding = #lwe.polynomial_evaluation_encoding<cleartext_start = 16, cleartext_bitwidth = 16>
!rns_L0_ = !rns.rns<!Z1095233372161_i64_>
!rns_L1_ = !rns.rns<!Z1095233372161_i64_, !Z1032955396097_i64_>
!rns_L2_ = !rns.rns<!Z1095233372161_i64_, !Z1032955396097_i64_, !Z1005037682689_i64_>
#ring_rns_L0_1_x8_ = #polynomial.ring<coefficientType = !rns_L0_, polynomialModulus = <1 + x**8>>
#ring_rns_L1_1_x8_ = #polynomial.ring<coefficientType = !rns_L1_, polynomialModulus = <1 + x**8>>
#ring_rns_L2_1_x8_ = #polynomial.ring<coefficientType = !rns_L2_, polynomialModulus = <1 + x**8>>
!rlwe_pt_L0_ = !lwe.rlwe_plaintext<encoding = #polynomial_evaluation_encoding, ring = #ring_rns_L0_1_x8_, underlying_type = i16>
!rlwe_pt_L1_ = !lwe.rlwe_plaintext<encoding = #polynomial_evaluation_encoding, ring = #ring_rns_L1_1_x8_, underlying_type = tensor<8xi16>>
!rlwe_pt_L2_ = !lwe.rlwe_plaintext<encoding = #polynomial_evaluation_encoding, ring = #ring_rns_L2_1_x8_, underlying_type = tensor<8xi16>>
#rlwe_params_L0_ = #lwe.rlwe_params<ring = #ring_rns_L0_1_x8_>
#rlwe_params_L1_ = #lwe.rlwe_params<ring = #ring_rns_L1_1_x8_>
#rlwe_params_L2_ = #lwe.rlwe_params<ring = #ring_rns_L2_1_x8_>
#rlwe_params_L2_D3_ = #lwe.rlwe_params<dimension = 3, ring = #ring_rns_L2_1_x8_>
!rlwe_ct_L0_ = !lwe.rlwe_ciphertext<encoding = #polynomial_evaluation_encoding, rlwe_params = #rlwe_params_L0_, underlying_type = i16>
!rlwe_ct_L1_ = !lwe.rlwe_ciphertext<encoding = #polynomial_evaluation_encoding, rlwe_params = #rlwe_params_L1_, underlying_type = tensor<8xi16>>
!rlwe_ct_L1_1 = !lwe.rlwe_ciphertext<encoding = #polynomial_evaluation_encoding, rlwe_params = #rlwe_params_L1_, underlying_type = i16>
!rlwe_ct_L2_ = !lwe.rlwe_ciphertext<encoding = #polynomial_evaluation_encoding, rlwe_params = #rlwe_params_L2_, underlying_type = tensor<8xi16>>
!rlwe_ct_L2_D3_ = !lwe.rlwe_ciphertext<encoding = #polynomial_evaluation_encoding, rlwe_params = #rlwe_params_L2_D3_, underlying_type = tensor<8xi16>>
module {
  func.func @dot_product(%arg0: !openfhe.crypto_context, %arg1: !rlwe_ct_L2_, %arg2: !rlwe_ct_L2_) -> !rlwe_ct_L0_ {
    %cst = arith.constant dense<[0, 0, 0, 0, 0, 0, 0, 1]> : tensor<8xi64>
    %0 = openfhe.mul_no_relin %arg0, %arg1, %arg2 : (!openfhe.crypto_context, !rlwe_ct_L2_, !rlwe_ct_L2_) -> !rlwe_ct_L2_D3_
    %1 = openfhe.relin %arg0, %0 : (!openfhe.crypto_context, !rlwe_ct_L2_D3_) -> !rlwe_ct_L2_
    %2 = openfhe.rot %arg0, %1 {index = 4 : index} : (!openfhe.crypto_context, !rlwe_ct_L2_) -> !rlwe_ct_L2_
    %3 = openfhe.add %arg0, %1, %2 : (!openfhe.crypto_context, !rlwe_ct_L2_, !rlwe_ct_L2_) -> !rlwe_ct_L2_
    %4 = openfhe.rot %arg0, %3 {index = 2 : index} : (!openfhe.crypto_context, !rlwe_ct_L2_) -> !rlwe_ct_L2_
    %5 = openfhe.add %arg0, %3, %4 : (!openfhe.crypto_context, !rlwe_ct_L2_, !rlwe_ct_L2_) -> !rlwe_ct_L2_
    %6 = openfhe.rot %arg0, %5 {index = 1 : index} : (!openfhe.crypto_context, !rlwe_ct_L2_) -> !rlwe_ct_L2_
    %7 = openfhe.add %arg0, %5, %6 : (!openfhe.crypto_context, !rlwe_ct_L2_, !rlwe_ct_L2_) -> !rlwe_ct_L2_
    %8 = openfhe.mod_reduce %arg0, %7 : (!openfhe.crypto_context, !rlwe_ct_L2_) -> !rlwe_ct_L1_
    %9 = openfhe.make_packed_plaintext %arg0, %cst : (!openfhe.crypto_context, tensor<8xi64>) -> !rlwe_pt_L1_
    %10 = openfhe.mul_plain %arg0, %8, %9 : (!openfhe.crypto_context, !rlwe_ct_L1_, !rlwe_pt_L1_) -> !rlwe_ct_L1_
    %11 = openfhe.rot %arg0, %10 {index = 7 : index} : (!openfhe.crypto_context, !rlwe_ct_L1_) -> !rlwe_ct_L1_
    %12 = lwe.reinterpret_application_data %11 : !rlwe_ct_L1_ to !rlwe_ct_L1_1
    %13 = openfhe.mod_reduce %arg0, %12 : (!openfhe.crypto_context, !rlwe_ct_L1_1) -> !rlwe_ct_L0_
    return %13 : !rlwe_ct_L0_
  }
  func.func @dot_product__encrypt__arg0(%arg0: !openfhe.crypto_context, %arg1: tensor<8xi16>, %arg2: !openfhe.public_key) -> !rlwe_ct_L2_ {
    ...
  }
  func.func @dot_product__encrypt__arg1(%arg0: !openfhe.crypto_context, %arg1: tensor<8xi16>, %arg2: !openfhe.public_key) -> !rlwe_ct_L2_ {
    ...
  }
  func.func @dot_product__decrypt__result0(%arg0: !openfhe.crypto_context, %arg1: !rlwe_ct_L0_, %arg2: !openfhe.private_key) -> i16 {
    ...
  }
  func.func @dot_product__generate_crypto_context() -> !openfhe.crypto_context {
    ...
  }
  func.func @dot_product__configure_crypto_context(%arg0: !openfhe.crypto_context, %arg1: !openfhe.private_key) -> !openfhe.crypto_context {
    ...
  }
}

Next, we use the heir-translate tool to run code generation for the OpenFHE pke API.

bazel run //tools:heir-translate -- --emit-openfhe-pke-header --openfhe-include-type=source-relative $PWD/output.mlir > heir_output.h
bazel run //tools:heir-translate -- --emit-openfhe-pke --openfhe-include-type=source-relative $PWD/output.mlir > heir_output.cpp

The openfhe-include-type indicates which include path for OpenFHE is used. It has three possible values: install-relative, source-relative and embedded. In this example we use source-relative as we are compiling against an (unoptimized) OpenFHE managed by bazel in HEIR source. To compile against an installed (and possibly optimized) OpenFHE, you could use install-relative and compile it on your own. Or you could just put the generated file in OpenFHE source directory src/pke/examples and let OpenFHE find and compile it for you with the embedded option.

The results:

// heir_output.h
#include "src/pke/include/openfhe.h"  // from @openfhe

using namespace lbcrypto;
using CiphertextT = ConstCiphertext<DCRTPoly>;
using CCParamsT = CCParams<CryptoContextBGVRNS>;
using CryptoContextT = CryptoContext<DCRTPoly>;
using EvalKeyT = EvalKey<DCRTPoly>;
using PlaintextT = Plaintext;
using PrivateKeyT = PrivateKey<DCRTPoly>;
using PublicKeyT = PublicKey<DCRTPoly>;

CiphertextT dot_product(CryptoContextT v0, CiphertextT v1, CiphertextT v2);
CiphertextT dot_product__encrypt__arg0(CryptoContextT v18, std::vector<int16_t> v19, PublicKeyT v20);
CiphertextT dot_product__encrypt__arg1(CryptoContextT v24, std::vector<int16_t> v25, PublicKeyT v26);
int16_t dot_product__decrypt__result0(CryptoContextT v30, CiphertextT v31, PrivateKeyT v32);
CryptoContextT dot_product__generate_crypto_context();
CryptoContextT dot_product__configure_crypto_context(CryptoContextT v37, PrivateKeyT v38);


// heir_output.cpp
#include "src/pke/include/openfhe.h"  // from @openfhe

using namespace lbcrypto;
using CiphertextT = ConstCiphertext<DCRTPoly>;
using CryptoContextT = CryptoContext<DCRTPoly>;
using EvalKeyT = EvalKey<DCRTPoly>;
using PlaintextT = Plaintext;
using PrivateKeyT = PrivateKey<DCRTPoly>;
using PublicKeyT = PublicKey<DCRTPoly>;

CiphertextT dot_product(CryptoContextT v0, CiphertextT v1, CiphertextT v2) {
  std::vector<int64_t> v3 = {0, 0, 0, 0, 0, 0, 0, 1};
  const auto& v4 = v0->EvalMultNoRelin(v1, v2);
  const auto& v5 = v0->Relinearize(v4);
  const auto& v6 = v0->EvalRotate(v5, 4);
  const auto& v7 = v0->EvalAdd(v5, v6);
  const auto& v8 = v0->EvalRotate(v7, 2);
  const auto& v9 = v0->EvalAdd(v7, v8);
  const auto& v10 = v0->EvalRotate(v9, 1);
  const auto& v11 = v0->EvalAdd(v9, v10);
  const auto& v12 = v0->ModReduce(v11);
  auto v3_filled_n = v0->GetCryptoParameters()->GetElementParams()->GetRingDimension() / 2;
  auto v3_filled = v3;
  v3_filled.clear();
  v3_filled.reserve(v3_filled_n);
  for (auto i = 0; i < v3_filled_n; ++i) {
    v3_filled.push_back(v3[i % v3.size()]);
  }
  const auto& v13 = v0->MakePackedPlaintext(v3_filled);
  const auto& v14 = v0->EvalMult(v12, v13);
  const auto& v15 = v0->EvalRotate(v14, 7);
  const auto& v16 = v15;
  const auto& v17 = v0->ModReduce(v16);
  return v17;
}
CiphertextT dot_product__encrypt__arg0(CryptoContextT v24, std::vector<int16_t> v25, PublicKeyT v26) {
  ...
}
CiphertextT dot_product__encrypt__arg1(CryptoContextT v29, std::vector<int16_t> v30, PublicKeyT v31) {
  ...
}
int16_t dot_product__decrypt__result0(CryptoContextT v34, CiphertextT v35, PrivateKeyT v36) {
  ...
}
CryptoContextT dot_product__generate_crypto_context() {
  ...
}
CryptoContextT dot_product__configure_crypto_context(CryptoContextT v37, PrivateKeyT v38) {
  ...
}

At this point we can compile the program as we would a normal OpenFHE program. Note that the above two files just contain the compiled function and encryption/decryption helpers, and does not include any code that provides specific inputs or calls these functions.

Next we’ll create a harness that provides sample inputs, encrypts them, runs the compiled function, and decrypts the result. Once you have the generated header and cpp files, you can do this with any build system. We will use bazel for consistency.

Create a file called BUILD in the same directory as the header and cpp files above, with the following contents:

# A library build target that encapsulates the HEIR-generated code.
cc_library(
    name = "dot_product_codegen",
    srcs = ["heir_output.cpp"],
    hdrs = ["heir_output.h"],
    deps = ["@openfhe//:pke"],
)

# An executable build target that contains your main function and links
# against the above.
cc_binary(
    name = "dot_product_main",
    srcs = ["dot_product_main.cpp"],
    deps = [
        ":dot_product_codegen",
        "@openfhe//:pke",
        "@openfhe//:core",
    ],
)

Where dot_product_main.cpp is a new file containing

#include <cstdint>
#include <vector>

#include "src/pke/include/openfhe.h"  // from @openfhe
#include "heir_output.h"

int main(int argc, char *argv[]) {
  CryptoContext<DCRTPoly> cryptoContext = dot_product__generate_crypto_context();

  KeyPair<DCRTPoly> keyPair;
  keyPair = cryptoContext->KeyGen();

  cryptoContext = dot_product__configure_crypto_context(cryptoContext, keyPair.secretKey);

  std::vector<int16_t> arg0 = {1, 2, 3, 4, 5, 6, 7, 8};
  std::vector<int16_t> arg1 = {2, 3, 4, 5, 6, 7, 8, 9};
  int64_t expected = 240;

  auto arg0Encrypted =
      dot_product__encrypt__arg0(cryptoContext, arg0, keyPair.publicKey);
  auto arg1Encrypted =
      dot_product__encrypt__arg1(cryptoContext, arg1, keyPair.publicKey);
  auto outputEncrypted =
      dot_product(cryptoContext, arg0Encrypted, arg1Encrypted);
  auto actual = dot_product__decrypt__result0(cryptoContext, outputEncrypted,
                                              keyPair.secretKey);

  std::cout << "Expected: " << expected << "\n";
  std::cout << "Actual: " << actual << "\n";

  return 0;
}

Then run and show the results:

$ bazel run dot_product_main
Expected: 240
Actual: 240

If you fetched a pre-built binary instead of building from source, then you will have to use your build system of choice to compile the generated files. If you use heir_py’s heir.compile decorator with debug=True, then the compilation commands will be printed to stdout so you can see how to compile the generated code manually.

Optional: Run a custom heir-opt pipeline

HEIR comes with two central binaries, heir-opt for running optimization passes and dialect conversions, and heir-translate for backend code generation. To see the list of available passes in each one, run the binary with --help:

bazel run //tools:heir-opt -- --help
bazel run //tools:heir-translate -- --help

Once you’ve chosen a pass or --pass-pipeline to run, execute it on the desired file. For example, you can run a test file through heir-opt to see its output. Note that when the binary is run via bazel, you must pass absolute paths to input files. You can also access the underlying binary at bazel-bin/tools/heir-opt, provided it has already been built.

bazel run //tools:heir-opt -- \
  --secret-to-cggi -cse \
  $PWD/tests/Dialect/Secret/Conversions/secret_to_cggi/add_one.mlir

To convert an existing lit test to a bazel run command for manual tweaking and introspection (e.g., adding --debug or --mlir-print-ir-after-all to see how he IR changes with each pass), use python scripts/lit_to_bazel.py.

# after pip install -r requirements.txt
python scripts/lit_to_bazel.py tests/simd/box_blur_64x64.mlir

Which outputs

bazel run --noallow_analysis_cache_discard //tools:heir-opt -- \
--secretize --wrap-generic --canonicalize --cse --full-loop-unroll \
--insert-rotate --cse --canonicalize --collapse-insertion-chains \
--canonicalize --cse /path/to/heir/tests/simd/box_blur_64x64.mlir

Optional: Graphviz visualization of the IR

Getting a visualization of the IR during optimization/transformation might help you understand what is going on more easily.

Still taking the dot_product_8.mlir as an example:

bazel run --ui_event_filters=-info,-debug,-warning,-stderr,-stdout --noshow_progress --logging=0 //tools:heir-opt -- --wrap-generic --heir-simd-vectorizer $PWD/tests/Examples/common/dot_product_8.mlir --view-op-graph 2> dot_product_8.dot
dot -Tpdf dot_product_8.dot > dot_product_8.pdf
# open pdf in your favorite pdf viewer

The diagram is also shown below. It demonstrates that the HEIR SIMD vectorizer would vectorize the dot-product program (tensor<8xi16>) then use rotate-and-reduce technique to compute the sum.

2 - Development

This guide and its sub-pages assume you have successfully built the HEIR project from source.

Contributing code to HEIR

The following steps should look familiar to typical workflows for pull request contributions. Feel free to consult GitHub Help if you need more information using pull requests. HEIR-specific processes begin at the pull request review stage.

Setup

  1. Fork the HEIR repository by clicking the Fork button on the repository page. This creates a copy of the HEIR repository on your own GitHub account, where you can make changes.

    Setting up git to work with fork and upstream remotes. If you have cloned your fork, you will want to add the HEIR repository as an upstream remote:
    git remote add upstream https://www.github.com/google/heir

    Alternatively, if you have cloned the main HEIR repo, you can add your fork as a remote like this:

    git remote rename origin upstream
git remote add origin https://www.github.com/<USERNAME>/heir

    Either way, you will want to create a development branch for your change:

    git checkout -b name-of-change

    In the remainder of this document, we will assume origin is your fork, and upstream is the main HEIR repo.

  2. Sign the Contributor License Agreement (CLA). If you are working on HEIR as part of your employment, you might have to instead sign a Corporate CLA. See more here.

Preparing a pull request

  1. Sync your changes against the upstream HEIR repository, i.e., make sure your contributions are (re)based of the most recent upstream/main commit.

  2. Check HEIR’s lint and style checks by running the following from the top of the repository:

    pre-commit run --all-files

If failed, check Pre-commit.

  1. Make sure tests are passing with the following:

    bazel test //...

  2. Once you are ready with your change, create a commit, e.g.:

    git add change.cpp
git commit -m "Detailed commit message"
git push --set-upstream origin name-of-change

Pull request review flow

  1. New PR:
  • When a new PR is submitted, it is inspected for quality requirements, such as the CLA requirement, and a sufficient PR description.
  • If the PR passes checks, we assign a reviewer. If not, we request additional changes to ensure the PR passes CI checks.
  1. Review
  • A reviewer will check the PR and potentially request additional changes.
  • If a change is needed, the contributor is requested to make a suggested change. Please make changes with additional commits to your PR, to ensure that the reviewer can easily see the diff.
  • If all looks good, the reviewer will approve the PR.
  • This cycle repeats itself until the PR is approved.
  1. Approved
  • At this stage, you must squash your commits into a single commit.
  • Once the PR is approved, a GitHub workflow will check your PR for multiple commits. You may use the git rebase -i to squash the commits. Pull requests must consist of a single git commit before merging.
  1. Pull Ready
  • Once the PR is squashed into a single git commit, a maintainer will apply the pull ready label.
  • This initiates the internal code migration and presubmits.
  • After the internal process is finished, the commit will be added to main and the PR closed as merged by that commit.

Internal review details

This diagram summarizes the GitHub/Google code synchronization process. This is largely automated by a Google-owned system called Copybara, the configuration for which is Google-internal. This system treats the Google-internal version of HEIR as the source of truth, and applies specified transformation rules to copy internal changes to GitHub and integrate external PRs internally.

Notable aspects:

  • The final merged code may differ slightly from a PR. The changes are mainly to support stricter internal requirements for BUILD files that we cannot reproduce externally due to minor differences between Google’s internal build systems and bazel that we don’t know how to align. Sometimes they will also include additional code quality fixes suggested by internal static analyzers that do not exist outside of Google.
  • Due to the above, signed commits with internal modifications will not maintain valid signatures after merging, which labels the commit with a warning.
  • You will see various actions taken on GitHub that include copybara in the name, such as changes that originate from Google engineers doing various approved migrations (e.g., migrating HEIR to support changes in MLIR or abseil).

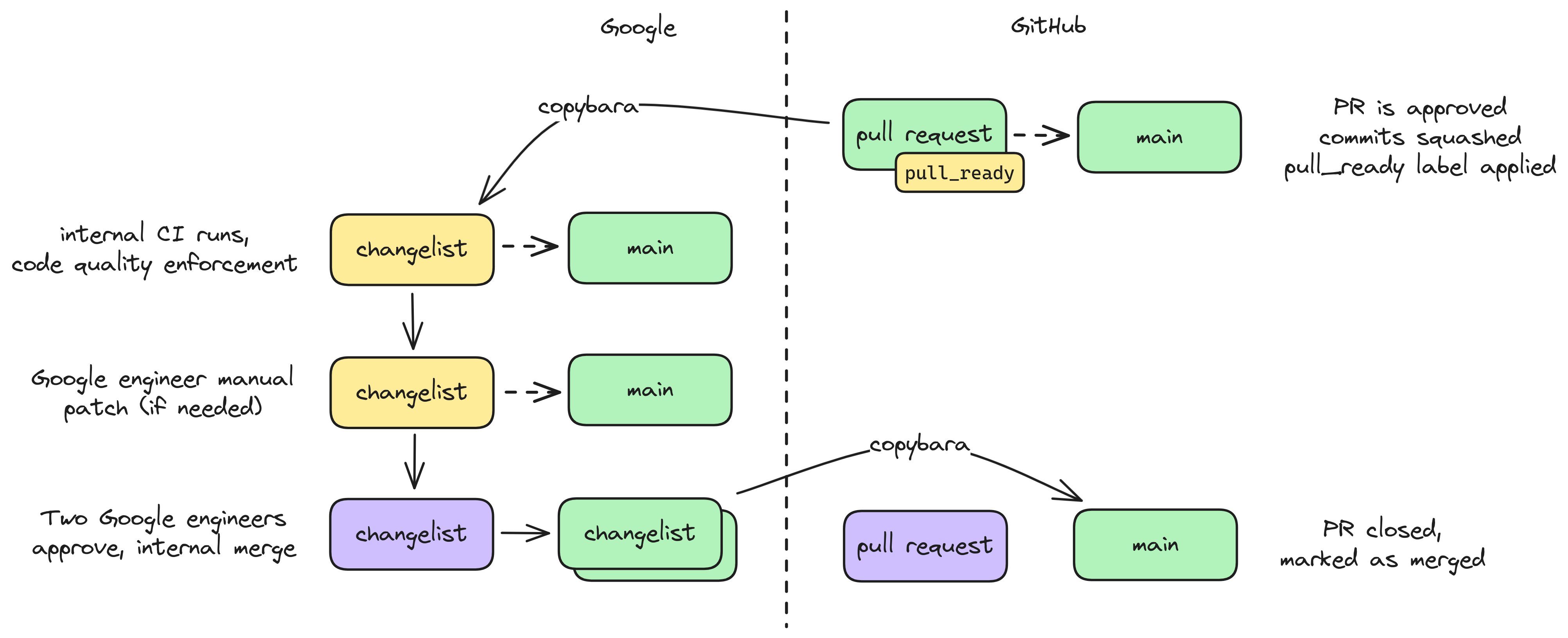
A diagram summarizing the copybara flow for HEIR internally to Google

Why bother with Copybara?

tl;dr: Automatic syncing with upstream MLIR and associated code migration.

Until HEIR has a formal governance structure in place, Google engineers—specifically Asra Ali, Shruthi Gorantala, and Jeremy Kun—are the codebase stewards. Because the project is young and the team is small, we want to reduce our workload. One important aspect of that is keeping up to date with the upstream MLIR project and incorporating bug fixes and new features into HEIR. Google also wishes to stay up to date with MLIR and LLVM, and so it has tooling devoted to integrating new MLIR changes into Google’s monorepo every few hours. As part of that rotation, a set of approved internal projects that depend on MLIR (like TensorFlow) are patched to support breaking changes in MLIR. HEIR is one of those approved projects.

As shown in the previous section, the cost of this is that no change can go into HEIR without at least two Googlers approving it, and the project is held to a specific set of code quality standards, namely Google’s. We acknowledge these quirks, and look forward to the day when HEIR is useful enough and important enough that we can revisit this governance structure with the community.

Pre-Commit

We use pre-commit to manage a series of git pre-commit hooks for the project; for example, each time you commit code, the hooks will make sure that your C++ is formatted properly. If your code isn’t, the hook will format it, so when you try to commit the second time you’ll get past the hook. Configuration for codespell, which catches spelling mistakes, is in pyproject.toml.

All hooks are defined in .pre-commit-config.yaml. To install these hooks, first run

pip install -r requirements.txt

You will also need to install ruby and go (e.g., apt-get install ruby golang) which are used by some of the pre-commits. Note that the pre-commit environment expects Python 3.11 (Installing python3.11 on ubuntu).

Then install the hooks to run automatically on git commit:

pre-commit install

To run them manually, run

pre-commit run --all-files

Tips for building dependencies / useful external libraries

Sometimes it is useful to point HEIR to external dependencies built according to the project’s usual build system, instead of HEIR’s bazel overlay. For example, to test upstream contributions to the dependency in the context of how it will be used in HEIR.

MLIR

Instructions for building MLIR can be found on the Getting started page of the MLIR website. The instructions there seem to work as written (tested on Ubuntu 22.04). However, the command shown in Unix-like compile/testing: may require a large amount of RAM. If building on a system with 16GB of RAM or less, and if you don’t plan to target GPUs, you may want to replace the line

   -DLLVM_TARGETS_TO_BUILD="Native;NVPTX;AMDGPU" \

with

   -DLLVM_TARGETS_TO_BUILD="Native" \

OpenFHE

A simple way to build OpenFHE is to follow the instructions in the openfhe-configurator repository. This allows to build the library with or without support for the Intel HEXL library which adds AVX512 support. First, clone the repository and configure it using:

git clone https://github.com/openfheorg/openfhe-configurator.git
cd openfhe-configurator
scripts/configure.sh

You will be asked whether to stage a vanilla OpenFHE build or add support for HEXL. You can then build the library using

./scripts/build-openfhe-development.sh

The build may fail on systems with less than 32GB or RAM due to parallel compilation. You can disable it by editing ./scripts/build-openfhe-development.sh and replacing

make -j || abort "Build of openfhe-development failed."

with

make || abort "Build of openfhe-development failed."

Compilation will be significantly slower but should then take less than 8GB of memory.

2.1 - Bazel tips

BUILD file formatting

The buildifier tool can be used to format BUILD files. You can download the latest Buildifier release from the Bazel Release Page. See IDE configuration for tips on integrating this with your IDE.

Avoiding rebuilds

Bazel is notoriously fickle when it comes to deciding whether a full rebuild is necessary, which is bad for HEIR because rebuilding LLVM from scratch takes 15 minutes or more. We try to avoid this as much as possible by setting default options in the project root’s .bazelrc.

The main things that cause a rebuild are:

  • A change to the .bazelrc that implicitly causes a flag change. Note HEIR has its own project-specific .bazelrc in the root directory.
  • A change to the command-line flags passed to bazel, e.g., -c opt vs -c dbg for optimization level and debug symbols. The default is -c dbg, and you may want to override this to optimize performance of generated code. For example, the OpenFHE backend generates much faster code when compiled with -c opt.
  • A change to relevant command-line variables, such as PATH, which is avoided by the incompatible_strict_action_env flag. Note activating a python virtualenv triggers a PATH change. The default is incompatible_strict_action_env=true, and you would override this in the event that you want your shell’s environment variables to change and be inherited by bazel.

Pointing HEIR to a local clone of llvm-project

Occasionally changes in HEIR will need to be made in tandem with upstream changes in MLIR. In particular, we occasionally find upstream bugs that only occur with HEIR passes, and we are the primary owners/users of the upstream polynomial dialect.

To tell bazel to use a local clone of llvm-project instead of a pinned commit hash, replace bazel/import_llvm.bzl with the following file:

cat > bazel/import_llvm.bzl << EOF
"""Provides the repository macro to import LLVM."""

def import_llvm(name):
    """Imports LLVM."""
    native.new_local_repository(
        name = name,
        # this BUILD file is intentionally empty, because the LLVM project
        # internally contains a set of bazel BUILD files overlaying the project.
        build_file_content = "# empty",
        path = "/path/to/llvm-project",
    )
EOF

The next bazel build will require a full rebuild if the checked-out LLVM commit differs from the pinned commit hash in bazel/import_llvm.bzl.

Note that you cannot reuse the LLVM CMake build artifacts in the bazel build. Based on what you’re trying to do, this may require some extra steps.

  • If you just want to run existing MLIR and HEIR tests against local llvm-project changes, you can run the tests from HEIR using bazel test @llvm-project//mlir/...:all. New lit tests can be added in llvm-project’s existing directories and tested this way without a rebuild.
  • If you add new CMake targets in llvm-project, then to incorporate them into HEIR you need to add new bazel targets in llvm-project/utils/bazel/llvm-project-overlay/mlir/BUILD.bazel. This is required if, for example, a new dialect or pass is added in MLIR upstream.

Send any upstream changes to HEIR-relevant MLIR files to @j2kun (Jeremy Kun) who has LLVM commit access and can also suggest additional MLIR reviewers.

Finding the right dependency targets

Whenever a new dependency is added in C++ or Tablegen, a new bazel BUILD dependency is required, which requires finding the path to the relevant target that provides the file you want. In HEIR the BUILD target should be defined in the same directory as the file you want to depend on (e.g., the targets that provide foo.h are in BUILD in the same directory), but upstream MLIR’s bazel layout is different.

LLVM’s bazel overlay for MLIR is contained in a single file, and so you can manually look there to find the right target. With bazel, if you know the filepath of interested you can also run:

bazel query --keep_going 'same_pkg_direct_rdeps(@llvm-project//mlir:<path>)'

where <path> is the path relative to mlir/ in the llvm-project project root. For example, to find the target that provides mlir/include/mlir/Pass/PassBase.td, run

bazel query --keep_going 'same_pkg_direct_rdeps(@llvm-project//mlir:include/mlir/Pass/PassBase.td)'

And the output will be something like

@llvm-project//mlir:PassBaseTdFiles

You can find more examples and alternative queries at the Bazel query docs.

2.2 - Boilerplate tools

The script scripts/templates/templates.py contains commands for generating new dialects and transforms, filling in most of the boilerplate Tablegen and C++. These commands do not add the code needed to register the new passes or dialects in heir-opt.

These should be used when the tablegen files containing existing pass definitions in the expected filepaths are not already present. Otherwise, you must modify the existing tablegen files directly.

Run python scripts/templates/templates.py --help and python scripts/templates/templates.py <subcommand> --help for the available commands and options.

Creating a New Pass

General passes

If the pass does not operate from and to a specific dialect, use something similar to:

python scripts/templates/templates.py new_transform \
--pass_name=ForgetSecrets \
--pass_flag=forget-secrets

Dialect Transforms

To create a pass that operates within on a dialect, run a command similar to:

python scripts/templates/templates.py new_dialect_transform \
--pass_name=ForgetSecrets \
--pass_flag=forget-secrets \
--dialect_name=Secret \
--dialect_namespace=secret

Conversion Pass

To create a new conversion pass, i.e., a pass that lowers from one dialect to another, run a command similar to:

python scripts/templates/templates.py new_conversion_pass \
--source_dialect_name=CGGI \
--source_dialect_namespace=cggi \
--source_dialect_mnemonic=cggi \
--target_dialect_name=TfheRust \
--target_dialect_namespace=tfhe_rust \
--target_dialect_mnemonic=tfhe_rust

In order to build the resulting code, you must fix the labeled FIXMEs in the type converter and the op conversion patterns.

Creating a New Dialect

To create a new dialect, run something like

python scripts/templates/templates.py new_dialect \
--dialet_name=TensorExt \
--dialect_namespace=tensor_ext \
--enable_attributes=False \
--enable_types=True \
--enable_ops=True

Note that all --enable flags are True by default, so if you know your dialect will not have attributes or types, you have to explicitly disable those options.

2.3 - IDE configuration

heir-lsp

HEIR provides an LSP server that extends the MLIR LSP server with HEIR’s dialects.

Build the LSP binary, then move it to a location on your path or point your IDE to bazel-bin/tools/heir-lsp.

bazel build //tools:heir-lsp
cp bazel-bin/tools/heir-lsp /usr/local/bin

Note that if you change any HEIR dialects, or if HEIR’s dependency on MLIR updates and the upstream MLIR has dialect changes (which happens roughly daily), you need to rebuild heir-lsp for it to recognize the changes.

clangd

Most IDE configured to use clangd can be powered from a file called compile_commands.json. To generate that for HEIR, run

bazel run @hedron_compile_commands//:refresh_all

This will need to be regenerated when there are major BUILD file changes. If you encounter errors like *.h.inc not found, or syntax errors inside these files, you may need to build those targets and then re-run the refresh_all command above.

Note that you will most likely also need to install the actual clangd language server, e.g., sudo apt-get install clangd on debian/ubuntu.

ibazel file watcher

ibazel is a shell around bazel that watches a build target for file changes and automatically rebuilds.

ibazel build //tools:heir-opt

VS Code

While a wide variety of IDEs and editors can be used for HEIR development, we currently only provide support for VSCode.

Setup

For the best experience, we recommend following these steps:

  • Install the MLIR, clangd and Bazel extensions

  • Install and rename Buildifier:

    You can download the latest Buildifier release, e.g., for linux-amd64 (see the Bazel Release Page for a list of available binaries):

    wget -c https://github.com/bazelbuild/buildtools/releases/latest/download/buildifier-linux-amd64
mv buildifier-linux-amd64 buildifier
chmod +x buildifier

    Just as with bazel, you will want to move this somewhere on your PATH, e.g.:

    mkdir -p ~/bin
echo 'export PATH=$PATH:~/bin' >> ~/.bashrc
mv buildifier ~/bin/buildifier

    VS Code should automatically detect buildifier. If this is not successful, you can manually set the “Buildifier Executable” setting for the Bazel extension (bazel.buildifierExecutable).

  • Disable the C/C++ (aka ‘cpptools’) extension (either completely, or in the current workspace).

  • Add the following snippet to your VS Code user settings found in .vscode/settings.json to enable autocomplete based on the compile_commands.json file (see above).

      "clangd.arguments": [
    "--compile-commands-dir=${workspaceFolder}/",
    "--completion-style=detailed",
    "--query-driver=**"
  ],

  • For Python formatting, HEIR uses pyink for autoformatting, which is a fork of the more commonly used black formatter with some patches to support Google’s internal style guide. To use it in VSCode, install pyink along with other python utilities needed for HEIR: pip install -r requirements.txt and install the Black Formatter extension, then add the following to your VSCode user settings (.vscode/settings.json):

    "[python]": {
    "editor.defaultFormatter": "ms-python.black-formatter"
},
"black-formatter.path": [
    "path/to/pyink"
]

  • It might be necessary to add the path to your buildifier to VSCode, though it should be auto-detected.

    • Open the heir folder in VSCode
    • Go to ‘Settings’ and set it on the ‘Workspace’
    • Search for “Bazel Buildifier Executable”
    • Once you find it, write [home-directory]/bin/buildifier for your specific [home-directory].

Building, Testing, Running and Debugging with VSCode

Building

  1. Open the “Explorer” (File Overview) in the left panel.
  2. Find “Bazel Build Targets” towards the bottom of the “Explorer” panel and click the dropdown button.
  3. Unfold the heir folder
  4. Right-click on “//tools” and click the “Build Package Recursively” option

Testing

  1. Open the “Explorer” (File Overview) in the left panel.
  2. Find “Bazel Build Targets” towards the bottom of the “Explorer” panel and click the dropdown button.
  3. Unfold the heir folder
  4. Right-click on “//test” and click the “Test Package Recursively” option

Running and Debugging

  1. Create a launch.json file in the .vscode folder, changing the "name" and "args" as required:

    {
    "version": "0.2.0",
    "configurations": [
        {
            "name": "Debug Secret->BGV",
            "preLaunchTask": "build",
            "type": "lldb",
            "request": "launch",
            "program": "${workspaceFolder}/bazel-bin/tools/heir-opt",
            "args": [
                "--secret-to-bgv",
                "--debug",
                "${workspaceFolder}/tests/secret_to_bgv/ops.mlir"
            ],
            "relativePathBase": "${workspaceFolder}",
            "sourceMap": {
                "proc/self/cwd": "${workspaceFolder}",
                "/proc/self/cwd": "${workspaceFolder}"
            }
        },
    ]
}

    You can add as many different configurations as necessary.

  2. Add Breakpoints to your program as desired.

  3. Open the Run/Debug panel on the left, select the desired configuration and run/debug it.

  • Note that you might have to hit “Enter” to proceed past the Bazel build. It might take several seconds between hitting “Enter” and the debug terminal opening.

Vim/Neovim

Misc config

Filetype detection

# ftdetect/mlir.vim
au BufRead,BufNewFile *.mlir setfiletype mlir

Buildifier integration

# ftplugin/bzl.vim
augroup AutoFormat
  autocmd!
  autocmd BufWritePre Neoformat buildifier
augroup END

LSP configuration (Neovim, using nvim-lspconfig)

nvim_lsp["mlir_lsp_server"].setup {
    on_attach = on_attach,
    capabilities = capabilities,
    cmd = { "heir-lsp" },
}

Tree-sitter configuration for relevant project languages

require('nvim-treesitter.configs').setup {
  ensure_installed = {
    "markdown_inline",  -- for markdown in tablegen
    "mlir",
    "tablegen",
    "verilog",  -- for yosys
  },

  -- <... other config options ...>
}

Telescope-alternate config (quickly jump between cc, header, and tablegen files)

require('telescope-alternate').setup({
  mappings = {
    {
      pattern = '**/(.*).h',
      targets = {
        { template = '**/[1].cc',       label = 'cc',       enable_new = false },
        { template = '**/[1].cpp',      label = 'cpp',      enable_new = false },
        { template = '**/[1]Test.cc',   label = 'cc Test',  enable_new = false },
        { template = '**/[1]Test.cpp',  label = 'cpp Test', enable_new = false },
        { template = '**/[1].td',       label = 'tablegen', enable_new = false },
      }
    },
    {
      pattern = '**/(.*).cc',
      targets = {
        { template = '**/[1].h',        label = 'header',   enable_new = false },
        { template = '**/[1].cpp',      label = 'cpp',      enable_new = false },
        { template = '**/[1]Test.cc',   label = 'cc Test',  enable_new = false },
        { template = '**/[1]Test.cpp',  label = 'cpp Test', enable_new = false },
        { template = '**/[1].td',       label = 'tablegen', enable_new = false },
      }
    },
    {
      pattern = '**/(.*).cpp',
      targets = {
        { template = '**/[1].h',        label = 'header',   enable_new = false },
        { template = '**/[1].cc',       label = 'cc',       enable_new = false },
        { template = '**/[1]Test.cc',   label = 'test',     enable_new = false },
        { template = '**/[1]Test.cpp',  label = 'test',     enable_new = false },
        { template = '**/[1].td',       label = 'tablegen', enable_new = false },
      }
    },
    {
      pattern = '**/(.*).td',
      targets = {
        { template = '**/[1].h',        label = 'header',   enable_new = false },
        { template = '**/[1].cc',       label = 'cc',       enable_new = false },
        { template = '**/[1].cpp',      label = 'cpp',      enable_new = false },
      }
    },
    {
      pattern = '(.*)Test.(.*)',
      targets = {
        { template = '**/[1].[2]', label = 'implementation', enable_new = false },
      }
    },
  },
  open_only_one_with = 'vertical_split',
})

Useful mappings

Navigate to the bazel build target for current file

vim.keymap.set('n', '<leader>eb', function()
  -- expand("%:p:h") gets the current filepath
  local buildfile = vim.fn.expand("%:p:h") .. "/BUILD"
  -- expand("%:t") gets the current filename with suffix.
  local target = vim.fn.expand("%:t")
  vim.api.nvim_command("botright vsplit " .. buildfile)
  vim.cmd("normal /" .. target .. vim.api.nvim_replace_termcodes("<CR>", true, true, true))
  vim.cmd("normal zz")
end,
  { noremap = true })

Set include guards according to HEIR style guide.

local function build_include_guard()
  -- project relative filepath
  local abs_path = vim.fn.expand("%")
  local rel_path = vim.fn.fnamemodify(abs_path, ":~:.")

  -- screaming case
  local upper = string.upper(rel_path)
  -- underscore separated
  local underscored = string.gsub(upper, "[./]", "_")
  -- trailing underscore
  return underscored .. "_"
end

-- mnemonic: fi = fix include (guard)
vim.keymap.set('n', '<leader>fi', function()
  local buf = vim.api.nvim_get_current_buf()
  local include_guard = build_include_guard()
  local ifndef = "#ifndef " .. include_guard
  local define = "#define " .. include_guard
  local endif = "#endif  // " .. include_guard

  vim.api.nvim_buf_set_lines(buf, 0, 2, false, { ifndef, define })
  vim.api.nvim_buf_set_lines(buf, -2, -1, false, { endif })
end, { noremap = true })

3 - Tutorials and Talks

A list of tutorials by the HEIR community. To add to this list, open an issue or submit a pull request on GitHub.

Talks

MLIR tutorials

FHE math

4 - Research with HEIR

Citing HEIR

HEIR: A Universal Compiler for Homomorphic Encryption

@misc{ali2025heir,
      title={HEIR: A Universal Compiler for Homomorphic Encryption},
      author={Asra Ali and Jaeho Choi and Bryant Gipson and Shruthi Gorantala
              and Jeremy Kun and Wouter Legiest and Lawrence Lim and Alexander
              Viand and Meron Zerihun Demissie and Hongren Zheng},
      year={2025},
      eprint={2508.11095},
      archivePrefix={arXiv},
      primaryClass={cs.CR},
      url={https://arxiv.org/abs/2508.11095},
}

Publications built on HEIR

Doing private research using HEIR

Our project will be developed in an open-source GitHub repository. If you’d like to work on a non-public branch while still accessing the latest developments, we recommend the following setup. This process will result in two remote repositories: one public for submitting pull requests (PRs) to the original repo and one private.

  1. Fork the Repository: Fork the google/heir repo to a public fork on your GitHub repository. This should create a project at https://github.com/<username>/heir

  2. Create a Private Repository: Create a new private repo using the GitHub UI, e.g. named heir-private

  3. Link Your Fork to the Private Repository Couple your fork to the new private repo

git clone --bare git@github.com:<username>/heir.git heir-public
cd heir-public
git push --mirror git@github.com:<username>/heir-private.git
cd ..
rm -rf heir-public
  1. Clone the Private Repository Now, you can clone the private repo to work locally
git clone git@github.com:<username>/heir-private.git
cd heir-private
  1. Add the Private Repository as a Remote to Your Public Repository Additionally, you can add the private repo as a remote target to your public repo. This way, the private branch will be locally available, while you can push commits to the private repo.
cd heir
git remote add private git@github.com:<username>/heir-private.git
git fetch --all
git checkout private/new_branch

Note that using git push private new_branch2 will push the commit/branch to the private repo.

Once you’re ready to publish your development work, you can push your commits to a branch in the public repository and create a pull request.

5 - Design

HEIR is a compiler toolchain that allows the compilation of high-level programs to equivalent programs that operate on encrypted data.

HEIR is built in the MLIR framework.

HEIR defines dialects at various layers of abstraction, from high-level scheme-agnostic operations on secret types to low-level polynomial arithmetic. The diagram below shows some of the core HEIR dialects, and the compilation flow is generally from the top of the diagram downward.

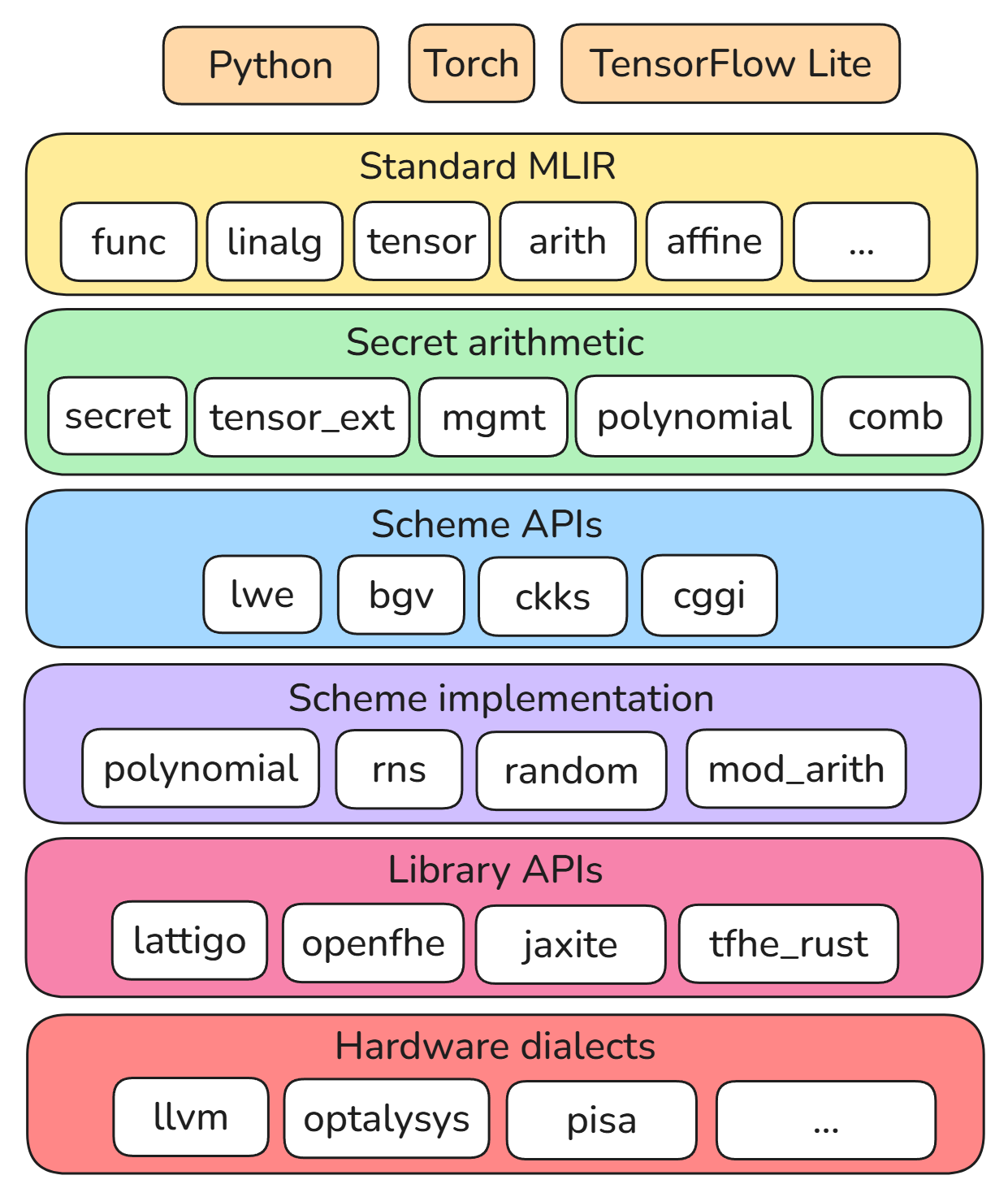
The pages in this section describe the design of various subcomponents of HEIR.

5.1 - Ciphertext Management

On 2025-04-17, Hongren Zheng gave a talk overview of the ciphertext management system in the HEIR working group meeting. The video can be found here and the slides can be found here

Introduction

To lower from user specified computation to FHE scheme operations, a compiler must insert ciphertext management operations to satisfy various requirements of the FHE scheme, like modulus switching, relinearization, and bootstrapping. In HEIR, such operations are modeled in a scheme-agnostic way in the mgmt dialect.

Taking the arithmetic pipeline as example: a program specified in high-level MLIR dialects like arith and linalg is first transformed to an IR with only arith.addi/addf, arith.muli/mulf, and tensor_ext.rotate operations. We call this form the secret arithmetic IR.

Then management passes insert mgmt ops to support future lowerings to scheme dialects like bgv and ckks. As different schemes have different management requirement, they should be inserted in different styles.

We discuss each scheme below to show the design in HEIR. For RLWE schemes, we all assume RNS instantiation.

BGV

BGV is a leveled scheme where each level has a modulus $q_i$. The level is numbered from $0$ to $L$ where $L$ is the input level and $0$ is the output level. The core feature of BGV is that when the magnititude of the noise becomes large (often caused by multiplication), a modulus switching operation from level $i$ to level $i-1$ can be inserted to reduce the noise to a “constant” level. In this way, BGV can support a circuit of multiplicative depth $L$.

BGV: Relinearization

HEIR initially inserts relinearization ops immediately after each multiplication to keep ciphertext dimension “linear”. A later relinearization optimization pass relaxes this requirement, and uses an integer linear program to decide when to relinearize. See Optimizing Relinearization for more details.

BGV: Modulus switching

There are several techniques to insert modulus switching ops.

For the example circuit input -> mult -> mult -> output, the insertion result could be one of

  1. After multiplication: input -> (mult -> ms) -> (mult -> ms) -> output

  2. Before multiplication: input -> (mult) -> (ms -> mult) -> (ms -> output)

  3. Before multiplication (including the first multiplication): input -> (ms -> mult) -> (ms -> mult) -> (ms -> output)

The first strategy is from the BGV paper, the second and third strategies are from OpenFHE, which correspond to the FLEXIBLEAUTO mode and FLEXIBLEAUTOEXT mode, respectively.

The first strategy is conceptually simpler, yet other policies have the advantage of smaller noise growth. In latter policies, by delaying the modulus switch until just before multiplication, the noise from other operations between multiplications (like rotation/relinearization) also benefit from the noise reduction of a modulus switch.

Note that, as multiplication has two operands, the actual circuit for the latter two policies is mult(ms(ct0), ms(ct1)), whereas in the first policy the circuit is ms(mult(ct0, ct1)).

The third policy has one more switching op than the others, so it will need one more modulus.

There are also other insertion strategy like inserting it dynamically based on current noise (see HElib) or lazy modulus switching. Those are not implemented.

BGV: Scale management

For the original BGV scheme, it is required to have $qi \equiv 1 \pmod{t}$ where $t$ is the plaintext modulus. However in practice such requirement will make the choice of $q_i$ too constrained. In the GHS variant, this condition is removed, with the price of scale management needed.

Modulus switching from level $i$ to level $i-1$ is essentially dividing (with rounding) the ciphertext by $q_i$, hence dividing the noise and payload message inside by $q_i$. The message $m$ can often be written as $[m]_t$, the coset representative of m $\mathbb{Z}/t\mathbb{Z}$. Then by dividing of $q_i$ produces a result message $[m \cdot q_i^{-1}]_t$.

Note that when $qi \equiv 1 \pmod{t}$, the result message is the same as the original message. However, in the GHS variant this does not always hold, so we call the introduced factor of $[q^{-1}]_t$ the scale of the message. HEIR needs to record and manage it during compilation. When decrypting the scale must be removed to obtain the right message.

Note that, for messages $m_0$ and $m_1$ of different scale $a$ and $b$, we cannot add them directly because $[a \cdot m_0 + b \cdot m_1]_t$ does not always equal $[m_0 + m_1]_t$. Instead we need to adjust the scale of one message to match the other, so $[b \cdot m_0 + b \cdot m_1]_t = [b \cdot (m_0 + m_1)]_t$. Such adjustment could be done by multiplying $m_0$ with a constant $[b \cdot a^{-1}]_t$. This adjustment is not for free, and increases the ciphertext noise.

As one may expect, different modulus switching insertion strategies affect message scale differently. For $m_0$ with scale $a$ and $m_1$ with scale $b$, the result scale would be

  1. After multiplication: $[ab / qi]_t$.

  2. Before multiplication: $[a / qi \cdot b / qi]_t = [ab / (qi^2)]_t$.

This is messy enough. To ease the burden, we can impose additional requirement: mandate a constant scale $\Delta_i$ for all ciphertext at level $i$. This is called the level-specific scaling factor. With this in mind, addition within one level can happen without caring about the scale.

  1. After multiplication: $\Delta_{i-1} = [\Delta_i^2 / qi]_t$

  2. Before multiplication: $\Delta_{i-1} = [\Delta_i^2 / (qi^2)]_t$

BGV: Cross Level Operation

With the level-specific scaling factor, one may wonder how to perform addition and multiplication of ciphertexts on different levels. This can be done by adjusting the level and scale of the ciphertext at the higher level.

The level can be easily adjusted by dropping the extra limbs, and scale can be adjusted by multiplying a constant, but because multiplying a constant will incur additional noise, the procedure becomes the following:

  1. Assume the level and scale of two ciphertexts are $l_1$ and $l_2$, $s_1$ and $s_2$ respectively. WLOG assume $l_1 > l_2$.

  2. Drop $l_1 - l_2 - 1$ limbs for the first ciphertext to make it at level $l_2 + 1$, if those extra limbs exist.

  3. Adjust scale from $s_1$ to $s_2 \cdot q_{l_2 + 1}$ by multiplying $[s_2 \cdot q_{l_2 + 1} / s1]_t$ for the first ciphertext.

  4. Modulus switch from $l_2 + 1$ to $l_2$, producing scale $s_2$ for the first ciphertext and its noise is controlled.

BGV: Implementation in HEIR

In HEIR the different modulus switching policy is controlled by the pass option for --secret-insert-mgmt-bgv. The pass defaults to the “Before Multiplication” policy. If user wants other policy, the after-mul or before-mul-include-first-mul option may be used. The mlir-to-bgv pipeline option modulus-switch-before-first-mul corresponds to the latter option.

The secret-insert-mgmt pass is also responsible for managing cross-level operations. However, as the scheme parameters are not generated at this point, the concrete scale could not be instantiated so some placeholder operations are inserted.

After the modulus switching policy is applied, the generate-param-bgv pass generates scheme parameters. Optionally, user could skip this pass by manually providing scheme parameter as an attribute at module level.

Then populate-scale-bgv comes into play by using the scheme parameters to instantiate concrete scale, and turn those placeholder operations into concrete multiplication operation.

CKKS

CKKS is a leveled scheme where each level has a modulus $q_i$. The level is numbered from $0$ to $L$ where $L$ is the input level and $0$ is the output level. CKKS ciphertext contains a scaled message $\Delta m$ where $\Delta$ takes some value like $2^40$ or $2^80$. After multiplication of two messages, the scaling factor $\Delta’$ will become larger, hence some kind of management policy is needed in case it blows up. Contrary to BGV where modulus switching is used for noise management, in CKKS modulus switching from level $i$ to level $i-1$ can divide the scaling factor $\Delta$ by the modulus $q_i$.

The management of CKKS is similar to BGV above in the sense that their strategy are the similar and uses similar code base. However, BGV scale management is internal and users are not required to concern about it, while CKKS scale management is visible to user as it affects the precision. One notable difference is that, for “Before multiplication (including the first multiplication)” modulus switching policy, the user input should be encoded at $\Delta^2$ or higher, as otherwise the first modulus switching (or rescaling in CKKS term) will rescale $\Delta$ to $1$, rendering full precision loss.

5.2 - Ciphertext Packing System

This document describes HEIR’s ciphertext packing system, including:

  • A notation and internal representation of a ciphertext packing, which we call a layout.
  • An abstraction layer to associate SSA values with layouts and manipulate and analyze them before a program is converted to concrete FHE operations.
  • A variety of layouts and kernels from the FHE literature.
  • A layout and kernel optimizer based on the Fhelipe compiler.
  • A layout conversion implementation of the Vos-Vos-Erkin graph coloring algorithm.

For background on what ciphertext packing is and its role in homomorphic encryption, see this introductory blog post. The short version of that blog post is that the SIMD-style HE computational model requires implementing linear-algebraic operations in terms of elementwise additions, multiplications, and cyclic rotations of large-dimensional vectors (with some exceptions like the Park-Gentry matrix-multiplication kernel).

Practical programs require many such operations, and the task of the compiler is to jointly choose ciphertext packings and operation kernels so as to minimize overall program latency. In this document we will call the joint process of optimizing layouts and kernels by the name “layout optimization.” In FHE programs, runtime primarily comes from the quantity of rotation and bootstrap operations, the latter of which is in turn approximated by multiplicative depth. Metrics like memory requirements may also be constrained, but for most of this document latency is the primary concern.

HEIR’s design goal is to be an extensible HE compiler framework, we aim to support a variety of layout optimizers and multiple layout representations. As such, we separate the design of the layout representation from the details of the layout optimizer, and implement lowerings for certain ops that can be reused across optimizers.

This document will begin by describing the layout representation, move on to the common, reusable components for working with that representation, and then finally describe one layout optimizer implemented in HEIR based on Fhelipe.

Layout representation

A layout is a description of how cleartext data is organized within a list of ciphertexts. In general, a layout is a partial function mapping from the index set of a list of ciphertext slots to the index set of a cleartext tensor. The function describes which cleartext data value is stored at which ciphertext slot.

A layout is partial because not all ciphertext slots need to be used, and the function uses ciphertext slots as the domain and cleartext indices as the codomain because cleartext values may be replicated among multiple slots, but a slot can store at most one cleartext value.

HEIR restricts the above definition of a layout as follows:

  • The partial function must be expressible as a Presburger relation, which will be defined in detail below.
  • Unmapped ciphertext slots always contain zero.

We claim that this subset of possible layouts is a superset of all layouts that have been used in the FHE literature to date. For example, both the layout notation of Fhelipe and the TileTensors of HeLayers are defined in terms of specific parameterized quasi-affine formulas.

Next we define a Presburger relation, then move on to examples.

Quasi-affine formulas and Presburger relations

Definition: A quasi-affine formula is a multivariate formula built from the following operations:

  • Integer literals
  • Integer-valued variables
  • addition and subtraction
  • multiplication by an integer constant
  • floor- and ceiling-rounded division by a nonzero integer constant
  • modulus by a nonzero integer constant

Using the BNF grammar from the MLIR website, we can also define it as

affine-expr ::= `(` affine-expr `)`
              | affine-expr `+` affine-expr
              | affine-expr `-` affine-expr
              | `-`? integer-literal `*` affine-expr
              | affine-expr `ceildiv` integer-literal
              | affine-expr `floordiv` integer-literal
              | affine-expr `mod` integer-literal
              | `-`affine-expr
              | bare-id
              | `-`? integer-literal

Definition: Let $d, r \in \mathbb{Z}_{\geq 0}$ represent a number of domain and range dimensions, respectively. A Presburger relation is a binary relation over $\mathbb{Z}^{d} \times \mathbb{Z}^{r}$ that can be expressed as the solution to a set of equality and inequality constraints defined using quasi-affine formulas.

We will use the Integer Set Library (ISL) notation to describe Presburger relations. For an introduction to the ISL notation and library, see this article. For a comprehensive reference, see the ISL manual.

Example 1: Given a data vector of type tensor<8xi32> and a ciphertext with 32 slots, a layout that repeats the tensor cyclically is given as:

{
    [d] -> [ct, slot] :
    0 <= d < 8
    and ct = 0
    and 0 <= slot < 32
    and (d - slot) mod 8 = 0
}

From Example 1, we note that in HEIR the domain of a layout always aligns with the shape of the domain tensor, and the range of a layout is always a 2D tensor whose first dimension denotes the ciphertext index and whose second index is the slot within that ciphertext.

Example 2: Given a data matrix of type tensor<8x8xi32> and 8 ciphertexts with 32 slots each, the following layout implements the standard Halevi-Shoup diagonal layout.

{
    [row, col] -> [ct, slot] :
    0 <= row < 8
    and 0 <= col < 8
    and 0 <= ct < 8
    and 0 <= slot < 32
    and (row - col + ct) mod 8 = 0
    and (row - slot) mod 32 = 0
}

Note, this layout implements a diagonal packing, and further replicates each diagonal cyclically within a ciphertext.

Layout attributes

Layouts are represented in HEIR via the tensor_ext.layout attribute. Its argument includes a string using the ISL notation above. For example

#tensor_layout = #tensor_ext.layout<
    "{ [i0] -> [ct, slot] : (slot - i0) mod 8 = 0 and ct = 0 and 1023 >= slot >= 0 and 7 >= i0 >= 0 }"
>

Generally, layout attributes are associated with an SSA value by being attached to the op that owns the SSA value. In MLIR, which op owns the value has two cases:

  • For an op result, the layout attribute is stored on the op.
  • For a block argument, the layout attribute is stored on the op owning the block, using the OperandAndResultAttrInterface to give a consistent API for accessing the attribute.

These two differences are handled properly by a helper library, lib/Utils/AttributeUtils.h, which exposes setters and getters for layout attributes. As of 2025-10-01, the system does not provide a way to handle ops with multiple regions or multi-block regions.

For example, #layout_attr is associated with the SSA value %1:

%1 = arith.addi %0, %1 {tensor_ext.layout = #layout_attr} : tensor<512xf32>

Data-semantic and ciphertext-semantic tensors

In HEIR, before lowering to scheme ops, we distinguish between types in two regimes:

  • Data-semantic tensors, which are scalars and tensors that represent cleartext data values, largely unchanged from the original input program.
  • Ciphertext-semantic tensors, which are rank-2 tensors that represent packed cleartext values in ciphertexts.

The task of analyzing an IR to determine which layouts and kernels to use happens in the data-semantic regime. In these passes, chosen layouts are persisted between passes as attributes on ops (see Layout attributes above), and data types are unchanged.

In this regime, there are three special tensor_ext ops that are no-ops on data-semantic type, but are designed to manipulate the layout attributes. These ops are:

  • tensor_ext.assign_layout, which takes a data-semantic value and a layout attribute, and produces the same data-semantic type. This is an “entry point” into the layout system and lowers to a loop that packs the data according to the layout.
  • tensor_ext.convert_layout, which makes an explicit conversion between a data-semantic value’s current layout and a new layout. Typically this lowers to a shift network.
  • tensor_ext.unpack, which clears the layout attribute on a data-semantic value, and serves as an exit point from the layout system. This lowers to a loop which extracts the packed cleartext data back into user data.

A layout optimizer is expected to insert assign_layout ops for any server-side cleartexts that need to be packed at runtime.

In the ciphertext-semantic regime, all secret values are rank-2 tensors whose first axis indexes ciphertexts and whose second axis indexes slots within ciphertexts. These tensors are subject to the constraints of the SIMD FHE computational model (elementwise adds, muls, and structured rotations), though the type system does not enforce this until secret-to-<scheme> lowerings, which would fail if encountering an op that cannot be implemented in FHE.

We preserve the use of the tensor type here, rather than create new types, so that we can reuse MLIR infrastructure. For example, if we were to use a new tensor-like type for ciphertext-semantic tensors, we would not be able to use arith.addi anymore, and would have to reimplement folding and canonicalization patterns from MLIR in HEIR. In the future we hope MLIR will relax these constraints via interfaces and traits, and at that point we could consider a specialized type.

Before going on, we note that the layout specification language is agnostic to how the “slots” are encoded in the underlying FHE scheme. In particular, slots could correspond to evaluation points of an RNS polynomial, i.e., to “NTT form” slots. But they could also correspond to the coefficients of an RNS polynomial in coefficient form. As of 2025-10-01, HEIR’s Fhelipe-inspired pipeline materializes slots as NTT-form slots in all cases, but is not required by the layout system. The only part of the layout system that depends on NTT-form is the implementation of operation kernels in terms of rotation operations, as coefficient-form ciphertexts do not have a rotation operation available. Future layout optimizers may take into account conversions between NTT and coefficient form as part of a layout conversion step.

HEIR’s Fhelipe-inspired layout optimizer

Pipeline overview

The mlir-to-<scheme> pipeline involves the following passes that manipulate layouts:

  • layout-propagation
  • layout-optimization
  • convert-to-ciphertext-semantics
  • implement-rotate-and-reduce
  • add-client-interface

The two passes that are closest to Fhelipe’s design are layout-propagation and layout-optimization. The former sets up initial default layouts for all values and default kernels for all ops that need them, and propagates them forward, inserting layout conversion ops as needed to resolve layout mismatches. The latter does a backwards pass, jointly choosing more optimal kernels and attempting to hoist layout conversions earlier in the IR. If layout conversions are hoisted all the way to function arguments then they are “free” because they can be merged into client preprocessing.

Next we will outline the responsibility of each pass in detail. The documentation page for each of these passes is linked in each section, and contains doctests as examples that are kept in sync with the implementation of the pass.

layout-propagation

The layout-propagation pass runs a forward pass through the IR to assign default layouts to each SSA value that needs one, and a default kernel to each operation that needs one.

For each secret-typed function argument, no layout can be inferred, so a default layout is assigned. The default layout for scalars is to repeat the scalar in every slot of a single ciphertext. The default layout for tensors is a row-major layout into as many ciphertexts as are needed to fit the tensor.

Then layouts are propagated forward through the IR. For each op, a default kernel is chosen, and if the layouts of the operands are already set and agree, the result layout is inferred according to the kernel.

If the layouts are not compatible with the default kernel, a convert_layout op is inserted to force compatibility. If one or more operands has a layout that is not set (which can happen if the operand is a cleartext value known to the server), then a compatible layout is chosen and an assign_layout op is inserted to persist this information for later passes.

Because layout-propagation may have inserted some redundant conversions, sequences of assign_layout followed by convert_layout are folded together into combined assign_layout ops.

layout-optimization

The layout-optimization pass has two main goals: to choose better kernels for ops, and to try to eliminate convert_layout ops. It does this by running a backward pass through the IR. If it encounters an op that is followed by a convert_layout op, it attempts to hoist the convert_layout through the op to its arguments.

In doing this, it must consider:

  • Changing the kernel of the op, and the cost of implementing the kernel. E.g., a new kernel may be better for the new layout of the operands.
  • Whether the new layout of op results still need to be converted, and the new cost of these conversions. E.g., if the op result has multiple uses, or the op result had multiple layout conversions, only one of which is hoisted.
  • The new cost of operand layout conversions. E.g., if a layout conversion is hoisted to one operand, it may require other operands to be converted to remain compatible.

In all of the above, the “cost” includes an estimate of the latency of a kernel, an estimate of the latency of a layout conversion, as well as the knowledge that some layout conversions may be free or cheaper because of their context in the IR.

NOTE: The cost of a kernel is currently considered free. This is mainly because we don’t have many different kernels for each op right now, so the choice of kernel is not very interesting.

TODO(#2316): implement a cost model for kernels

The cost of a layout conversion is estimated by simulating what the implement-shift-network would do if it ran on a layout conversion. And layout-optimization includes analyses that allow it to determine a folded cost for layout conversions that occur after other layout conversions, as well as the free cost of layout conversions that occur at function arguments, after assign_layout ops, or separated from these by ops that do not modify a layout.

After the backward pass, any remaining convert_layout ops at the top of a function are hoisted into function arguments and folded into existing layout attributes.

convert-to-ciphertext-semantics

The convert-to-ciphertext-semantics pass has two responsibilities that must happen at the same time:

  • Converting all data-semantic values to ciphertext-semantic values with corresponding types.
  • Implementing FHE kernels for all ops as chosen by earlier passes.

After this pass is complete, the IR must be in the ciphertext-semantic regime and all operations on secret-typed values must be constrained by the SIMD FHE computational model.

In particular, this pass implements assign_layout as an explicit loop that packs cleartext data into ciphertext slots according to the layout attribute. It also implements convert_layout as a shift network, which is a sequence of plaintext masks and rotations that can arbitrarily (albeit expensively) shuffle data in slots. This step can be isolated via the implement-shift-network pass, but the functionality is inlined in this pass since it must happen at the same time as type conversion.

When converting function arguments, any secret-typed argument is assigned a new attribute called tensor_ext.original_type, which records the original data-semantic type of the argument as well as the layout used for its packing. This is used later by the add-client-interface pass to generate client-side encryption and decryption helper functions.

implement-rotate-and-reduce

Some kernels rely on a baby-step giant-step optimization, and defer the implementation of that operation so that canonicalization patterns can optimize them. Instead they emit a tensor_ext.rotate_and_reduce op. The implement-rotate-and-reduce pass implements this op using baby-step giant-step, or other approaches that are relevant to special cases.

add-client-interface

The add-client-interface pass inserts additional functions that can be used by the client to encrypt and decrypt data according to the layouts chosen by the layout optimizer.

It fetches the original_type attribute on function arguments, and generates an encryption helper function for each secret argument, and a decryption helper function for each secret return type.

These helper functions use secret.conceal and secret.reveal for scheme-agnostic encryption and decryption, but eagerly implement the packing logic as a loop, equivalently to how assign_layout is lowered in convert-to-ciphertext-semantics, and adding an analogous lowering for tensor_ext.unpack.

Reusable components for working with layouts

Lowering data-semantic ops with FHE kernels

Any layout optimizer will eventually need to convert data-semantic values to ciphertext-semantic tensors. In doing this, all kernels need to be implemented in one pass at the same time that the types are converted.

The convert-to-ciphertext-semantics pass implements this conversion without making any decisions about which layouts or kernels to use. In particular, for ops that have multiple supported kernels, it picks the kernel to use based on the kernel attribute on the op (cf. secret::SecretDialect::kKernelAttrName).

In this way, we decouple the decision of which layout and kernel to use (the optimizer’s job) from the implementation of that kernel (the lowering’s job). Ideally all layout optimizer pipelines can reuse this pass, which avoids the common pitfalls associated with writing dialect conversion passes. New kernels, similarly, can be primarily implemented as described in the next section.

Finally, if a new optimizer or layout notation is introduced into HEIR, it should ultimately be converted to use the same tensor_ext.layout attribute so that it can reuse the lowerings of ops like tensor_ext.assign_layout and tensor_ext.unpack.

Testing kernels and layouts

Writing kernels can be tricky, so HEIR provides a simplified framework for implementing kernels which allows them to be unit-tested in isolation, while the lowering to MLIR is handled automatically by a common library.

The implementation library is called ArithmeticDag. Some initial implementations are in lib/Kernel/KernelImplementation.h, and example unit tests are in lib/Kernel/*Test.cpp. Then a class called IRMaterializingVisitor walks the DAG and generates MLIR code.

Similarly, lib/Utils/Layout/Evaluate.h provides helper functions to materialize layouts on test data-semantic tensors, which can be combined with ArithmeticDag to unit-test a layout and kernel combination without ever touching MLIR.

Manipulating layouts

The directory lib/Utils/Layout contains a variety of helper code for manipulating layout relations, including:

  • Constructing or testing for common kinds of layouts, such as row-major, diagonal, and layouts related to particular machine learning ops like convolution.
  • Generating explicit loops that iterate over the space of points in a layout, which is used to generate packing and unpacking code.
  • Helpers for hoisting layout conversions through ops.

These are implemented using two APIs: one is the Fast Presburger Library (FPL), which is part of MLIR and includes useful operations like composing relations and projecting out dimensions. The other is the Integer Set Library (ISL), which is a more fully-featured library that supports code generation and advanced analyses and simplification routines. As we represent layouts as ISL strings, we include a two-way interoperability layer that converts between ISL and FPL representations of the same Presburger relation.

A case study: the Orion convolution kernel

The Orion compiler presents a kernel for 2D convolution that first converts the filter input into a Toeplitz matrix $A$, and then applies a Halevi-Shoup diagonal packing and kernel on $A$ using the encrypted image vector $v$ packed row-major into a single ciphertext.

We describe how this layout is constructed and represented in HEIR.

The first, analytical step, is to describe a Presburger relation mapping a cleartext filter matrix to the Toeplitz matrix form as described in the Orion paper. Essentially, this involves writing down the loop nest that implements a convolution and, for each visited index,

Let $P$ be an integer padding value, fix stride 1, and define $i_{dr}, i_{dc}$ to be indices over the “data row” and “data column”, respectively, i.e., these variables track the top-left index of the filter as it slides over the convolved image in the data-semantic domain. For an image of height $H_d$ and width $W_d$, and a filter of height $H_f$ and width $W_f$, we have

$$ -P \leq i_{dr} \leq H_d + P - W_f $$

and similarly for $i_{dc}$.

Then we have bounds for the iteration of entries of the filter itself, for a fixed position of the filter over the image. If we consider these local variables $i_{fr}$ and $i_{fc}$ for “filter row” and “filter column”, respectively, we have

$$ 0 \leq i_{fr} < H_f $$

and similarly for $i_{fc}$.

From these two indices we can compute the corresponding entry of the data matrix that is being operated on as $i_{dr} + i_{fr}$ and $i_{dc} + i_{fc}$. If that index is within the bounds of the image, then the filter entry at that position is included in the Toeplitz matrix.

Finally, we need to compute the row and column of the Toeplitz matrix that each filter entry maps to. This is the novel part of the Orion construction. Each row of the Toeplitz matrix corresponds to one iteration over the filter (the filter is fixed at some position of the filter over the image). And the column value is a flattened index of the filter entry, plus offsets from both the padding and the iteration of the filter over the image (each step the filter moves adds one more to the offset).

The formula for the target row is

$$ m_{r} = (i_{dr} + P) F + i_{dc} + P $$

where $F$ is the total number of positions the filter assumes within each row, i.e., $F = H_d + 2P - H_f + 1$.

And the target column is

$$ m_{c} = W_d i_{dr} + i_{dc} + W_d i_{fr} + i_{fc} $$

Note the use of W_d for both the offset from the filter’s position over the image, and the offset from the filter’s own row.

Together this produces the following almost-Presburger relation:

[Hd, Wd, Hf, Wf, P] -> {
    [ifr, ifc] -> [mr, mc] : exists idr, idc :

    // Bound the top-left index of the filter as it slides over the image
    -P <= idr <= Hd + P - Hf
    and -P <= idc <= Wd + P - Wf

    // Bound the index within the filter
    and 0 <= ifr < Hf
    and 0 <= ifc < Wf

    // Only map values when the filter index is in bounds
    and 0 <= ifr + idr < Hd
    and 0 <= ifc + idc < Wd

    // Map the materialized filter index to its position in the Toeplitz matrix
    and mr = (idr + P) * (Wd + 2P - Wf + 1) + idc + P
    and mc = (idr * Wd + idc) + Wd * ifr + ifc
}

This is “almost” a Presburger relation because, even though the symbol variables Hd, Wd, Hf, Wf, and P are all integer constants, they cannot be multiplied together in a Presburger formula. But if we replace them with specific constants, such as

Hd = 8
Wd = 8
Hf = 3
Wf = 3
P = 1

We get

{
    [ifr, ifc] -> [mr, mc] : exists idr, idc :
    -1 <= idr <= 6
    and -1 <= idc <= 6
    and 0 <= ifr < 3
    and 0 <= ifc < 3
    and 0 <= ifr + idr < 8
    and 0 <= ifc + idc < 8
    and mr = (idr + 1) * 8 + idc + 1
    and mc = idr * 8 + idc + ifc + ifr * 8
}

Which ISL simplifies to

{
    [ifr, ifc] -> [mr, mc = -9 + 8ifr + ifc + mr] :
    0 <= ifr <= 2
    and 0 <= ifc <= 2
    and mr >= 0
    and 8 - 8ifr <= mr <= 71 - 8ifr
    and mr <= 63
    and 8*floor((mr)/8) >= -8 + ifc + mr
    and 8*floor((mr)/8) < ifc + mr
}

Next, we can compose the above relation with the Halevi-Shoup diagonal layout (using FPL’s IntegerRelation::compose), to get a complete layout from filter entries to ciphertext slots. Using ciphertexts with 1024 slots, we get:

{
    [ifr, ifc] -> [ct, slot] :
    (9 - 8ifr - ifc + ct) mod 64 = 0
    and 0 <= ifr <= 2
    and 0 <= ifc <= 2
    and 0 <= ct <= 63
    and 0 <= slot <= 1023
    and 8*floor((slot)/8) >= -8 + ifc + slot
    and 8*floor((slot)/8) < ifc + slot
    and 64*floor((slot)/64) >= -72 + 8ifr + ifc + slot
    and 64*floor((slot)/64) >= -71 + 8ifr + slot
    and 64*floor((slot)/64) <= -8 + 8ifr + slot
    and 64*floor((slot)/64) <= -9 + 8ifr + ifc + slot
}

FAQ

Can users define kernels without modifying the compiler?

No (as of 2025-10-01). However, a kernel DSL is in scope for HEIR. Reach out if you’d like to be involved in the design.

5.3 - Data-oblivious Transformations

A data-oblivious program is one that decouples data input from program execution. Such programs exhibit control-flow and memory access patterns that are independent of their input(s). This programming model, when applied to encrypted data, is necessary for expressing FHE programs. There are 3 major transformations applied to convert a conventional program into a data-oblivious program:

(1) If-Transformation

If-operations conditioned on inputs create data-dependent control-flow in programs. scf.if operations should at least define a ’then’ region (true path) and always terminate with scf.yield even when scf.if doesn’t produce a result. To convert a data-dependent scf.if operation to an equivalent set of data-oblivious operations in MLIR, we hoist all safely speculatable operations in the scf.if operation and convert the scf.yield operation to an arith.select operation. The following code snippet demonstrates an application of this transformation.

// Before applying If-transformation
func.func @my_function(%input : i1 {secret.secret}) -> () {
  ...
  // Violation: %input is used as a condition causing a data-dependent branch
  %result =`%input -> (i16) {
        %a = arith.muli %b, %c : i16
        scf.yield %a : i16
      } else {
        scf.yield %b : i16
      }
  ...
}

// After applying If-transformation
func.func @my_function(%input : i16 {secret.secret}) -> (){
  ...
  %a = arith.muli %b, %c : i16
  %result = arith.select %input, %a, %b : i16
  ...
}

We implement a ConvertIfToSelect pass that transforms operations with secret-input conditions and with only Pure operations (i.e., operations that have no memory side effect and are speculatable) in their body. This transformation cannot be applied to operations when side effects are present in only one of the two regions. Although possible, we currently do not support transformations for operations where both regions have operations with matching side effects. When side effects are present, the pass fails.

(2) Loop-Transformation

Loop statements with input-dependent conditions (bounds) and number of iterations introduce data-dependent branches that violate data-obliviousness. To convert such loops into a data-oblivious version, we replace input-dependent conditionals (bounds) with static input-independent parameters (e.g. defining a constant upper bound), and early-exits with update operations where the value returned from the loop is selectively updated using conditional predication. In MLIR, loops are expressed using either affine.for, scf.for or scf.while operations.

[!NOTE] Early exiting from loops is not supported in scf and affine, so early exits are not supported in this pipeline. Early exits are expected to be added to MLIR upstream at some point in the future.

  • affine.for: This operation lends itself well to expressing data oblivious programs because it requires constant loop bounds, eliminating input-dependent limits.
 %sum_0 = arith.constant 0.0 : f32
 // The for-loop's bound is a fixed constant
 %sum = affine.for %i = 0 to 10 step 2
 iter_args(%sum_iter = %sum_0) -> (f32) {
   %t = affine.load %buffer[%i] : memref<1024xf32>
   %sum_next = arith.addf %sum_iter, %input : f32
   affine.yield %sum_next : f32
 }
 ...
  • scf.for: In contrast to affine.for, scf.for does allow input-dependent conditionals which does not adhere to data-obliviousness constraints. A solution to this could be to either have the programmer or the compiler specify an input-independent upper bound so we can transform the loop to use this upper bound and also carefully update values returned from the for-loop using conditional predication. Our current solution to this is for the programmer to add the lower bound and worst case upper bound in the static affine loop’s attributes list.
func.func @my_function(%value: i32 {secret.secret}, %inputIndex: index {secret.secret}) -> i32 {
  ...
  // Violation: for-loop uses %inputIndex as upper bound which causes a secret-dependent control-flow
  %result = scf.for %iv = %begin to %inputIndex step %step_value iter_args(%arg1 = %value) -> i32 {
    %output = arith.muli %arg1, %arg1 : i32
    scf.yield %output : i32
  }{lower = 0, upper = 32}
  ...
}

// After applying Loop-Transformation
func.func @my_function(%value: i32 {secret.secret}, %inputIndex: index {secret.secret}) -> i32 {
  ...
  // Build for-loop using lower and upper values from the `attributes` list
  %result = affine.for %iv = 0 to  step 32 iter_args(%arg1 = %value) -> i32 {
    %output = arith.muli %arg1, %agr1 : i32
    %cond = arith.cmpi eq, %iv, %inputIndex : index
    %newOutput = arith.select %cond, %output, %arg1
    scf.yield %newOutput : i32
    }
  ...
}
  • scf.while: This operation represents a generic while/do-while loop that keeps iterating as long as a condition is met. An input-dependent while condition introduces a data-dependent control flow that violates data-oblivious constraints. For this transformation, the programmer needs to add the max_iter attribute that describes the maximum number of iterations the loop runs which we then use the value to build our static affine.for loop.
// Before applying Loop-Transformation
func.func @my_function(%input: i16 {secret.secret}){
  %zero = arith.constant 0 : i16
  %result = scf.while (%arg1 = %input) : (i16) -> i16 {
    %cond = arith.cmpi slt, %arg1, %zero : i16
    // Violation: scf.while uses %cond whose value depends on %input
    scf.condition(%cond) %arg1 : i16
  } do {
  ^bb0(%arg2: i16):
    %mul = arith.muli %arg2, %arg2: i16
    scf.yield %mul
  } attributes {max_iter = 16 : i64}
  ...
  return
}

// After applying Loop-Transformation
func.func @my_function(%input: i16 {secret.secret}){
  %zero = arith.constant 0 : i16
  %begin = arith.constant 1 : index
  ...
  // Replace while-loop with a for-loop with a constant bound %MAX_ITER
  %result = affine.for %iv = %0 to %16 step %step_value iter_args(%iter_arg = %input) -> i16 {
    %cond = arith.cmpi slt, %iter_arg, %zero : i16
    %mul = arith.muli %iter_arg, %iter_arg : i16
    %output = arith.select %cond, %mul, %iter_arg
    scf.yield %output
  }{max_iter = 16 : i64}
  ...
  return
}

(3) Access-Transformation

Input-dependent memory access cause data-dependent memory footprints. A naive data-oblivious solution to this maybe doing read-write operations over the entire data structure while only performing the desired save/update operation for the index of interest. For simplicity, we only look at load/store operations for tensors as they are well supported structures in high-level MLIR likely emitted by most frontends. We drafted the following non-SIMD approach for this transformation and defer SIMD optimizations to the heir-simd-vectorizer pass:

// Before applying Access Transformation
func.func @my_function(%input: tensor<16xi32> {secret.secret}, %inputIndex: index {secret.secret}) {
  ...
  %c_10 = arith.constant 10 : i32
  // Violation: tensor.extract loads value at %inputIndex
  %extractedValue = tensor.extract %input[%inputIndex] : tensor<16xi32>
  %newValue = arith.addi %extractedValue, %c_10 : i32
  // Violation: tensor.insert stores value at %inputIndex
  %inserted = tensor.insert %newValue into %input[%inputIndex] : tensor<16xi32>
  ...
}

// After applying Non-SIMD Access Transformation
func.func @my_function(%input: tensor<16xi32> {secret.secret}, %inputIndex: index {secret.secret}) {
  ...
  %c_10 = arith.constant 10 : i32
  %i_0 = arith.constant 0 : index
  %dummyValue = arith.constant 0 : i32

  %extractedValue = affine.for %i=0 to 16 iter_args(%arg= %dummyValue) -> (i32) {
    // 1. Check if %i matches %inputIndex
    // 2. Extract value at %i
    // 3. If %i matches %inputIndex, select %value extracted in (2), else select %dummyValue
    // 4. Yield selected value
    %cond = arith.cmpi eq, %i, %inputIndex : index
    %value = tensor.extract %input[%i] : tensor<16xi32>
    %selected = arith.select %cond, %value, %dummyValue : i32
    affine.yield %selected : i32
  }

  %newValue = arith.addi %extractedValue, %c_10 : i32

  %inserted = affine.for %i=0 to 16 iter_args(%inputArg = %input) -> tensor<16xi32> {
    // 1. Check if %i matches the %inputIndex
    // 2. Insert %newValue and produce %newTensor
    // 3. If %i matches %inputIndex, select %newTensor, else select input tensor
    // 4. Yield final tensor
    %cond = arith.cmpi eq, %i, %inputIndex : index
    %newTensor = tensor.insert %value into %inputArg[%i] : tensor<16xi32>
    %finalTensor= arith.select %cond, %newTensor, %inputArg : tensor<16xi32>
    affine.yield %finalTensor : tensor<16xi32>
  }
  ...
}

More notes on these transformations

These 3 transformations have a cascading behavior where transformations can be applied progressively to achieve a data-oblivious program. The order of the transformations goes as follows:

  • Access-Transformation (change data-dependent tensor accesses (reads-writes) to use affine.for and scf.if operations) -> Loop-Transformation (change data-dependent loops to use constant bounds and condition the loop’s yield results with scf.if operation) -> If-Transformation (substitute data-dependent conditionals with arith.select operation).
  • Besides that, when we apply non-SIMD Access-Transformation on multiple data-dependent tensor read-write operations over the same tensor, we can benefit from upstream affine transformations over the resulting multiple affine loops produced by the Access-Transformation to fuse these loops.

5.4 - Noise Analysis

Homomorphic Encryption (HE) schemes based on Learning-With-Errors (LWE) and Ring-LWE naturally need to deal with noises. HE compilers, in particular, need to understand the noise behavior to ensure correctness and security while pursuing efficiency and optimizaiton.

The noise analysis in HEIR has the following central task: Given an HE circuit, analyse the noise growth for each operation. HEIR then uses noise analysis for parameter selection, but the details of that are beyond the scope of this document.

Noise analysis and parameter generation are still under active researching and HEIR does not have a one-size-fits-all solution for now. Noise analyses and (especially) parameter generation in HEIR should be viewed as experimental. There is no guarantee that they are correct or secure and the HEIR authors do not take responsibility. Please consult experts before putting them into production.

Two Flavors of Noise Analysis

Each HE ciphertext contains noise. A noise analysis determines a bound on the noise and tracks its evolution after each HE operation. The noise should not exceed certain bounds imposed by HE schemes.

There are two flavors of noise analyses: worst-case and average-case. Worst-case noise analyses always track the bound, while some average-case noise analyses use intermediate quantity like the variance to track their evolution, and derive a bound when needed.

Currently, worst-case methods are often too conservative, while average-case methods often give underestimation.

Noise Analysis Framework

HEIR implements noise analysis based on the DataFlowFramework in MLIR.

In the DataFlowFramework, the main function of an Analysis is visitOperation, where it determines the AnalysisState for each SSA Value. Usually it computes a transfer function deriving the AnalysisState for each operation result based on the states of the operation’s operands.

As there are various HE schemes in HEIR, the detailed transfer function is defined by a NoiseModel class, which parameterizes the NoiseAnalysis.

The AnalysisState, depending on whether we are using worst-case noise model or average-case, could be interpreted as the bound or the variance.

A typical way to use noise analysis:

#include "mlir/include/mlir/Analysis/DataFlow/Utils.h"  // from @llvm-project

DataFlowSolver solver;
dataflow::loadBaselineAnalyses(solver);
// load other dependent analyses

// schemeParam and model determined by other methods
solver.load<NoiseAnalysis<NoiseModel>>(schemeParam, model);

// run the analysis on the op
solver.initializeAndRun(op)

Implemented Noise Models

See the Passes page for details. Example passes include generate-param-bgv and validate-noise.

5.5 - Secret

The secret dialect contains types and operations to represent generic computations on secret data. It is intended to be a high-level entry point for the HEIR compiler, agnostic of any particular FHE scheme.

Most prior FHE compiler projects design their IR around a specific FHE scheme, and provide dedicated IR types for the secret analogues of existing data types, and/or dedicated operations on secret data types. For example, the Concrete compiler has !FHE.eint<32> for an encrypted 32-bit integer, and add_eint and similar ops. HECO has !fhe.secret<T> that models a generic secret type, but similarly defines fhe.add and fhe.multiply, and other projects are similar.

The problem with this approach is that it is difficult to incorporate the apply upstream canonicalization and optimization passes to these ops. For example, the arith dialect in MLIR has canonicalization patterns that must be replicated to apply to FHE analogues. One of the goals of HEIR is to reuse as much upstream infrastructure as possible, and so this led us to design the secret dialect to have both generic types and generic computations. Thus, the secret dialect has two main parts: a secret<T> type that wraps any other MLIR type T, and a secret.generic op that lifts any computation on cleartext to the “corresponding” computation on secret data types.

Overview with BGV-style lowering pipeline

Here is an example of a program that uses secret to lift a dot product computation:

func.func @dot_product(
    %arg0: !secret.secret<tensor<8xi16>>,
    %arg1: !secret.secret<tensor<8xi16>>) -> !secret.secret<i16> {
  %c0_i16 = arith.constant 0 : i16
  %0 = secret.generic(%arg0, %arg1 : !secret.secret<tensor<8xi16>>, !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>, %arg3: tensor<8xi16>):
    %1 = affine.for %arg4 = 0 to 8 iter_args(%arg5 = %c0_i16) -> (i16) {
      %extracted = tensor.extract %arg2[%arg4] : tensor<8xi16>
      %extracted_0 = tensor.extract %arg3[%arg4] : tensor<8xi16>
      %2 = arith.muli %extracted, %extracted_0 : i16
      %3 = arith.addi %arg5, %2 : i16
      affine.yield %3 : i16
    }
    secret.yield %1 : i16
  } -> !secret.secret<i16>
  return %0 : !secret.secret<i16>
}

The operands to the generic op are the secret data types, and the op contains a single region, whose block arguments are the corresponding cleartext data values. Then the region is free to perform any computation, and the values passed to secret.yield are lifted back to secret types. Note that secret.generic is not isolated from its enclosing scope, so one may refer to cleartext SSA values without adding them as generic operands and block arguments.

Clearly secret.generic does not actually do anything. It is not decrypting data. It is merely describing the operation that one wishes to apply to the secret data in more familiar terms. It is a structural operation, primarily used to demarcate which operations involve secret operands and have secret results, and group them for later optimization. The benefit of this is that one can write optimization passes on types and ops that are not aware of secret, and they will naturally match on the bodies of generic ops.

For example, here is what the above dot product computation looks like after applying the -cse -canonicalize -heir-simd-vectorizer passes, the implementations of which do not depend on secret or generic.

func.func @dot_product(
    %arg0: !secret.secret<tensor<8xi16>>,
    %arg1: !secret.secret<tensor<8xi16>>) -> !secret.secret<i16> {
  %c1 = arith.constant 1 : index
  %c2 = arith.constant 2 : index
  %c4 = arith.constant 4 : index
  %c7 = arith.constant 7 : index
  %0 = secret.generic(%arg0, %arg1 : !secret.secret<tensor<8xi16>>, !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>, %arg3: tensor<8xi16>):
    %1 = arith.muli %arg2, %arg3 : tensor<8xi16>
    %2 = tensor_ext.rotate %1, %c4 : tensor<8xi16>, index
    %3 = arith.addi %1, %2 : tensor<8xi16>
    %4 = tensor_ext.rotate %3, %c2 : tensor<8xi16>, index
    %5 = arith.addi %3, %4 : tensor<8xi16>
    %6 = tensor_ext.rotate %5, %c1 : tensor<8xi16>, index
    %7 = arith.addi %5, %6 : tensor<8xi16>
    %extracted = tensor.extract %7[%c7] : tensor<8xi16>
    secret.yield %extracted : i16
  } -> !secret.secret<i16>
  return %0 : !secret.secret<i16>
}

The canonicalization patterns for secret.generic apply a variety of simplifications, such as:

  • Removing any unused or non-secret arguments and return values.
  • Hoisting operations in the body of a generic that only depend on cleartext values to the enclosing scope.
  • Removing any generic ops that use no secrets at all.

These can be used together with the secret-distribute-generic pass to split an IR that contains a large generic op into generic ops that contain a single op, which can then be lowered to a particular FHE scheme dialect with dedicated ops. This makes lowering easier because it gives direct access to the secret version of each type that is used as input to an individual op.

As an example, a single-op secret might look like this (taken from the larger example below. Note the use of a cleartext from the enclosing scope, and the proximity of the secret type to the op to be lowered.

  %c2 = arith.constant 2 : index
  %3 = secret.generic(%2 : !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>):
    %8 = tensor_ext.rotate %arg2, %c2 : tensor<8xi16>, index
    secret.yield %8 : tensor<8xi16>
  } -> !secret.secret<tensor<8xi16>>

For a larger example, applying --secret-distribute-generic --canonicalize to the IR above:

func.func @dot_product(%arg0: !secret.secret<tensor<8xi16>>, %arg1: !secret.secret<tensor<8xi16>>) -> !secret.secret<i16> {
  %c1 = arith.constant 1 : index
  %c2 = arith.constant 2 : index
  %c4 = arith.constant 4 : index
  %c7 = arith.constant 7 : index
  %0 = secret.generic(%arg0, %arg1 : !secret.secret<tensor<8xi16>>, !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>, %arg3: tensor<8xi16>):
    %8 = arith.muli %arg2, %arg3 : tensor<8xi16>
    secret.yield %8 : tensor<8xi16>
  } -> !secret.secret<tensor<8xi16>>
  %1 = secret.generic(%0 : !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>):
    %8 = tensor_ext.rotate %arg2, %c4 : tensor<8xi16>, index
    secret.yield %8 : tensor<8xi16>
  } -> !secret.secret<tensor<8xi16>>
  %2 = secret.generic(%0, %1 : !secret.secret<tensor<8xi16>>, !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>, %arg3: tensor<8xi16>):
    %8 = arith.addi %arg2, %arg3 : tensor<8xi16>
    secret.yield %8 : tensor<8xi16>
  } -> !secret.secret<tensor<8xi16>>
  %3 = secret.generic(%2 : !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>):
    %8 = tensor_ext.rotate %arg2, %c2 : tensor<8xi16>, index
    secret.yield %8 : tensor<8xi16>
  } -> !secret.secret<tensor<8xi16>>
  %4 = secret.generic(%2, %3 : !secret.secret<tensor<8xi16>>, !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>, %arg3: tensor<8xi16>):
    %8 = arith.addi %arg2, %arg3 : tensor<8xi16>
    secret.yield %8 : tensor<8xi16>
  } -> !secret.secret<tensor<8xi16>>
  %5 = secret.generic(%4 : !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>):
    %8 = tensor_ext.rotate %arg2, %c1 : tensor<8xi16>, index
    secret.yield %8 : tensor<8xi16>
  } -> !secret.secret<tensor<8xi16>>
  %6 = secret.generic(%4, %5 : !secret.secret<tensor<8xi16>>, !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>, %arg3: tensor<8xi16>):
    %8 = arith.addi %arg2, %arg3 : tensor<8xi16>
    secret.yield %8 : tensor<8xi16>
  } -> !secret.secret<tensor<8xi16>>
  %7 = secret.generic(%6 : !secret.secret<tensor<8xi16>>) {
  ^bb0(%arg2: tensor<8xi16>):
    %extracted = tensor.extract %arg2[%c7] : tensor<8xi16>
    secret.yield %extracted : i16
  } -> !secret.secret<i16>
  return %7 : !secret.secret<i16>
}

And then lowering it to bgv with --secret-to-bgv="poly-mod-degree=8" (the pass option matches the tensor size, but it is an unrealistic FHE polynomial degree used here just for demonstration purposes). Note type annotations on ops are omitted for brevity.

#encoding = #lwe.polynomial_evaluation_encoding<cleartext_start = 16, cleartext_bitwidth = 16>
#params = #lwe.rlwe_params<ring = <cmod=463187969, ideal=#_polynomial.polynomial<1 + x**8>>>
!ty1 = !lwe.rlwe_ciphertext<encoding=#encoding, rlwe_params=#params, underlying_type=tensor<8xi16>>
!ty2 = !lwe.rlwe_ciphertext<encoding=#encoding, rlwe_params=#params, underlying_type=i16>

func.func @dot_product(%arg0: !ty1, %arg1: !ty1) -> !ty2 {
  %c1 = arith.constant 1 : index
  %c2 = arith.constant 2 : index
  %c4 = arith.constant 4 : index
  %c7 = arith.constant 7 : index
  %0 = bgv.mul %arg0, %arg1
  %1 = bgv.relinearize %0 {from_basis = array<i32: 0, 1, 2>, to_basis = array<i32: 0, 1>}
  %2 = bgv.rotate %1, %c4
  %3 = bgv.add %1, %2
  %4 = bgv.rotate %3, %c2
  %5 = bgv.add %3, %4
  %6 = bgv.rotate %5, %c1
  %7 = bgv.add %5, %6
  %8 = bgv.extract %7, %c7
  return %8
}

Differences for CGGI-style pipeline

The mlir-to-cggi and related pipelines add a few additional steps. The main goal here is to apply a hardware circuit optimizer to blocks of standard MLIR code (inside secret.generic ops) which converts the computation to an optimized boolean circuit with a desired set of gates. Only then is -secret-distribute-generic applied to split the ops up and lower them to the cggi dialect. In particular, because passing an IR through the circuit optimizer requires unrolling all loops, one useful thing you might want to do is to optimize only the body of a for loop nest.

To accomplish this, we have two additional mechanisms. One is the pass option ops-to-distribute for -secret-distribute-generic, which allows the user to specify a list of ops that generic should be split across, and all others left alone. Specifying affine.for here will pass generic through the affine.for loop, but leave its body intact. This can also be used with the -unroll-factor option to the -yosys-optimizer pass to partially unroll a loop nest and pass the partially-unrolled body through the circuit optimizer.

The other mechanism is the secret.separator op, which is a purely structural op that demarcates the boundary of a subset of a block that should be jointly optimized in the circuit optimizer.

For example, the following tosa ops lower to multiple linalg instructions, and hence multiple for loops, that we want to pass to a circuit optimizer as a unit. The secret.separator ops surrounding the op are preserved through the lowering.

func.func @main(%arg0: tensor<1x1xi8> {secret.secret}) -> tensor<1x16xi32> {
  secret.separator
  %4 = "tosa.const"() {value = dense<[0, 0, -5438, -5515, -1352, -1500, -4152, -84, 3396, 0, 1981, -5581, 0, -6964, 3407, -7217]> : tensor<16xi32>} : () -> tensor<16xi32>
  %5 = "tosa.const"() {value = dense<[[-9], [-54], [57], [71], [104], [115], [98], [99], [64], [-26], [127], [25], [-82], [68], [95], [86]]> : tensor<16x1xi8>} : () -> tensor<16x1xi8>
  %6 = "tosa.matmul"(%arg0, %arg1) {a_zp = 1 : i32, b_zp = 2 : i32} : (tensor<1x5x3xi8>, tensor<1x3x6xi8>) -> tensor<1x5x6xi32>
  secret.separator
  return %6 : tensor<1x16xi32>
}

After running --mlir-to-cggi and dumping the IR after the linalg ops are lowered to loops, we can see the secret.separator ops enclose the lowered ops, with the exception of some pure ops that are speculatively executed.

func.func @main(%arg0: memref<1x1xi8, strided<[?, ?], offset: ?>> {secret.secret}) -> memref<1x16xi32> {
  %c-128_i32 = arith.constant -128 : i32
  %0 = memref.get_global @__constant_16xi32 : memref<16xi32>
  %1 = memref.get_global @__constant_16x1xi8 : memref<16x1xi8>
  secret.separator
  %alloc = memref.alloc() {alignment = 64 : i64} : memref<1x16xi8>
  affine.for %arg1 = 0 to 1 {
    affine.for %arg2 = 0 to 16 {
      %2 = affine.load %1[%arg2, %arg1] : memref<16x1xi8>
      affine.store %2, %alloc[%arg1, %arg2] : memref<1x16xi8>
    }
  }
  %alloc_0 = memref.alloc() {alignment = 64 : i64} : memref<1x16xi32>
  affine.for %arg1 = 0 to 1 {
    affine.for %arg2 = 0 to 16 {
      %2 = affine.load %0[%arg2] : memref<16xi32>
      affine.store %2, %alloc_0[%arg1, %arg2] : memref<1x16xi32>
    }
  }
  affine.for %arg1 = 0 to 1 {
    affine.for %arg2 = 0 to 16 {
      affine.for %arg3 = 0 to 1 {
        %2 = affine.load %arg0[%arg1, %arg3] : memref<1x1xi8, strided<[?, ?], offset: ?>>
        %3 = affine.load %alloc[%arg3, %arg2] : memref<1x16xi8>
        %4 = affine.load %alloc_0[%arg1, %arg2] : memref<1x16xi32>
        %5 = arith.extsi %2 : i8 to i32
        %6 = arith.subi %5, %c-128_i32 : i32
        %7 = arith.extsi %3 : i8 to i32
        %8 = arith.muli %6, %7 : i32
        %9 = arith.addi %4, %8 : i32
        affine.store %9, %alloc_0[%arg1, %arg2] : memref<1x16xi32>
      }
    }
  }
  secret.separator
  memref.dealloc %alloc : memref<1x16xi8>
  return %alloc_0 : memref<1x16xi32>
}

We decided to use the separator op over a few alternatives:

  • Grouping by secret.generic: these tosa ops must be bufferized, but secret types cannot participate in bufferization (see the Limitations section).
  • Grouping by basic blocks: secret.generic is a single-block op with a yield terminator, and grouping by blocks would require us to change this.
  • Grouping by regions: SSA values generated by a region are not visible to the enclosing scope, so we would need to have the region-bearing op return values, which is tedious to organize.
  • Attaching attributes to ops that should be grouped together: this would not be preserved by upstream lowerings and optimization passes.

generic operands

secret.generic takes any SSA values as legal operands. They may be secret types or non-secret. Canonicalizing secret.generic removes non-secret operands and leaves them to be referenced via the enclosing scope (secret.generic is not IsolatedFromAbove).

This may be unintuitive, as one might expect that only secret types are valid arguments to secret.generic, and that a verifier might assert non-secret args are not present.

However, we allow non-secret operands because it provides a convenient scope encapsulation mechanism, which is useful for the --yosys-optimizer pass that runs a circuit optimizer on individual secret.generic ops and needs to have access to all SSA values used as inputs. The following passes are related to this functionality:

  • secret-capture-generic-ambient-scope
  • secret-generic-absorb-constants
  • secret-extract-generic-body

Due to the canonicalization rules for secret.generic, anyone using these passes as an IR organization mechanism must be sure not to canonicalize before accomplishing the intended task.

Limitations

Bufferization

Secret types cannot participate in bufferization passes. In particular, -one-shot-bufferize hard-codes the notion of tensor and memref types, and so it cannot currently operate on secret<tensor<...>> or secret<memref<...>> types, which prevents us from implementing a bufferization interface for secret.generic. This was part of the motivation to introduce secret.separator, because tosa ops like a fully connected neural network layer lower to multiple linalg ops, and these ops need to be bufferized before they can be lowered further. However, we want to keep the lowered ops grouped together for circuit optimization (e.g., fusing transposes and constant weights into the optimized layer), but because of this limitation, we can’t simply wrap the tosa ops in a secret.generic (bufferization would fail).

5.6 - SIMD Optimizations

HEIR includes a SIMD (Single Instruction, Multiple Data) optimizer which is designed to exploit the restricted SIMD parallelism most (Ring-LWE-based) FHE schemes support (also commonly known as “packing” or “batching”). Specifically, HEIR incorporates the “automated batching” optimizations (among many other things) from the HECO compiler. The following will assume basic familiarity with the FHE SIMD paradigm and the high-level goals of the optimization, and we refer to the associated HECO paper, slides, talk and additional resources on the Usenix'23 website for an introduction to the topic. This documentation will mostly focus on describing how the optimization is realized in HEIR (which differs somewhat from the original implementation) and how the optimization is intended to be used in an overall end-to-end compilation pipeline.

Representing FHE SIMD Operations

Following the design principle of maintaining programs in standard MLIR dialects as long as possible (cf. the design rationale behind the Secret Dialect), HEIR uses the MLIR tensor dialect and ElementwiseMappable operations from the MLIR arith dialect to represent HE SIMD operations.

We do introduce the HEIR-specific tensor_ext.rotate operation, which represents a cyclical left-rotation of a tensor. Note that, as the current SIMD vectorizer only supports one-dimensional tensors, the semantics of this operation on multi-dimensional tensors are not (currently) defined.

For example, the common “rotate-and-reduce” pattern which results in each element containing the sum/product/etc of the original vector can be expressed as:

%tensor = tensor.from_elements %i1, %i2, %i3, %i4, %i5, %i6, %i7, %i8 : tensor<8xi16>
%0 = tensor_ext.rotate %tensor, %c4 : tensor<8xi16>, index
%1 = arith.addi %tensor, %0 : tensor<8xi16>
%2 = tensor_ext.rotate %1, %c2 : tensor<8xi16>, index
%3 = arith.addi %1, %2 : tensor<8xi16>
%4 = tensor_ext.rotate %3, %c1 : tensor<8xi16>, index
%5 = arith.addi %3, %4 : tensor<8xi16>

The %cN and %iN, which are defined as %cN = arith.constant N : index and %iN = arith.constant N : i16, respectively, have been omitted for readability.

Intended Usage

The -heir-simd-vectorizer pipeline transforms a program consisting of loops and index-based accesses into tensors (e.g., tensor.extract and tensor.insert) into one consisting of SIMD operations (including rotations) on entire tensors. While its implementation does not depend on any FHE-specific details or even the Secret dialect, this transformation is likely only useful when lowering a high-level program to an arithmetic-circuit-based FHE scheme (e.g., B/FV, BGV, or CKKS). The --mlir-to-bgv --scheme-to-openfhe pipeline demonstrates the intended flow: augmenting a high-level program with secret annotations, then applying the SIMD optimization (and any other high-level optimizations) before lowering to BGV operations and then exiting to OpenFHE.

Warning The current SIMD vectorizer pipeline supports only one-dimensional tensors. As a workaround, one could reshape all multi-dimensional tensors into one-dimensional tensors, but MLIR/HEIR currently do not provide a pass to automate this process.

Since the optimization is based on heuristics, the resulting program might not be optimal or could even be worse than a trivial realization that does not use ciphertext packing. However, well-structured programs generally lower to reasonable batched solutions, even if they do not achieve optimal batching layouts. For common operations such as matrix-vector or matrix-matrix multiplications, state-of-the-art approaches require advanced packing schemes that might map elements into the ciphertext vector in non-trivial ways (e.g., diagonal-major and/or replicated). The current SIMD vectorizer will never change the arrangement of elements inside an input tensor and therefore cannot produce the optimal approaches for these operations.

Note, that the SIMD batching optimization is different from, and significantly more complex than, the Straight Line Vectorizer (-straight-line-vectorize pass), which simply groups ElementwiseMappable operations that agree in operation name and operand/result types into vectorized/tensorized versions.

Implementation

Below, we give a brief overview over the implementation, with the goal of both improving maintainability/extensibility of the SIMD vectorizer and allowing advanced users to better understand why a certain program is transformed in the way it is.

Components

The -heir-simd-vectorizer pipeline uses a combination of standard MLIR passes (-canonicalize, -cse, -sccp) and custom HEIR passes. Some of these (-apply-folders, -full-loop-unroll) might have applications outside the SIMD optimization, while others (-insert-rotate, -collapse-insertion-chains and -rotate-and-reduce) are very specific to the FHE SIMD optimization. In addition, the passes make use of the RotationAnalysis and TargetSlotAnalysis analyses.

High-Level Flow

  • Loop Unrolling (-full-loop-unroll): The implementation currently begins by unrolling all loops in the program to simplify the later passes. See #589 for a discussion on how this could be avoided.

  • Canonicalization (-apply-folders -canonicalize): As the rotation-specific passes are very strict about the structure of the IR they operate on, we must first simplify away things such as tensors of constant values. For performance reasons (c.f. comments in the heirSIMDVectorizerPipelineBuilder function in heir-opt.cpp), this must be done by first applying folds before applying the full canonicalization.

  • Main SIMD Rewrite (-insert-rotate -cse -canonicalize -cse): This pass rewrites arithmetic operations over tensor.extract-ed operands into SIMD operations over the entire tensor, rotating the (full-tensor) operands so that the correct elements interact. For example, it will rewrite the following snippet (which computes t2[4] = t0[3] + t1[5])

    %0 = tensor.extract %t0[%c3] : tensor<32xi16>
%1 = tensor.extract %t1[%c5] : tensor<32xi16>
%2 = arith.addi %0, %1 : i16
%3 = tensor.insert %2 into %t2[%c4] : tensor<32xi16>

    to

    %0 = tensor_ext.rotate %t0, %c31 : tensor<32xi16>, index
%1 = tensor_ext.rotate %t1, %c1 : tensor<32xi16>, index
%2 = arith.addi %0, %1 : tensor<32xi16>

    i.e., rotating t0 down by one (31 = -1 (mod 32)) and t1 up by one to bring the elements at index 3 and 5, respectively, to the “target” index 4. The pass uses the TargetSlotAnalysis to identify the appropriate target index (or ciphertext “slot” in FHE-speak). See Insert Rotate Pass below for more details. This pass is roughly equivalent to the -batching pass in the original HECO implementation.

    Doing this rewrite by itself does not represent an optimization, but if we consider what happens to the corresponding code for other indices (e.g., t2[5] = t0[4] + t1[6]), we see that the pass transforms expressions with the same relative index offsets into the exact same set of rotations/SIMD operations, so the following Common Subexpression Elimination (CSE) will remove redundant computations. We apply CSE twice, once directly (which creates new opportunities for canonicalization and folding) and then again after that canonicalization. See TensorExt Canonicalization for a description of the rotation-specific canonocalization patterns).

  • Cleanup of Redundant Insert/Extract (-collapse-insertion-chains -sccp -canonicalize -cse): Because the -insert-rotate pass maintains the consistency of the IR, it emits a tensor.extract operation after the SIMD operation and uses that to replace the original operation (which is valid, as both produce the desired scalar result). As a consequence, the generated code for the snippet above is actually trailed by a (redundant) extract/insert:

    %extracted = tensor.extract %2[%c4] : tensor<32xi16>
%inserted = tensor.insert %extracted into %t2[%c4] : tensor<32xi16>

    In real code, this might generate a long series of such extraction/insertion operations, all extracting from the same (due to CSE) tensor and inserting into the same output tensor. Therefore, the -collapse-insertion-chains pass searches for such chains over entire tensors and collapses them. It supports not just chains where the indices match perfectly, but any chain where the relative offset is consistent across the tensor, issuing a rotation to realize the offset (if the offset is zero, the canonicalization will remove the redundant rotation). Note, that in HECO, insertion/extraction is handled differently, as HECO features a combine operation modelling not just simple insertions (combine(%t0#j, %t1)) but also more complex operations over slices of tensors (combine(%t0#[i,j], %t1)). As a result, the equivalent pass in HECO (-combine-simplify) instead joins different combine operations, and a later fold removes combines that replace the entire target tensor. See issue #512 for a discussion on why the combine operation is a more powerful framework and what would be necessary to port it to HEIR.

  • Applying Rotate-and-Reduce Patterns (-rotate-and-reduce -sccp -canonicalize -cse): The rotate and reduce pattern (see Representing FHE SIMD Operations for an example) is an important aspect of accelerating SIMD-style operations in FHE, but it does not follow automatically from the batching rewrites applied so far. As a result, the -rotate-and-reduce pass needs to search for sequences of arithmetic operations that correspond to the full folding of a tensor, i.e., patterns such as t[0]+(t[1]+(t[2]+t[3]+(...))), which currently uses a backwards search through the IR, but could be achieved more efficiently through a data flow analysis (c.f. issue #532). In HECO, rotate-and-reduce is handled differently, by identifying sequences of compatible operations prior to batching and rewriting them to “n-ary” operations. However, this approach requires non-standard arithmetic operations and is therefore not suitable for use in HEIR. However, there is likely still an opportunity to make the patterns in HEIR more robust/general (e.g., support constant scalar operands in the fold, or support non-full-tensor folds). See issue #522 for ideas on how to make the HEIR pattern more robust/more general.

Insert Rotate Pass

TODO(#721): Write a detailed description of the rotation insertion pass and the associated target slot analysis.

TensorExt Canonicalization

The TensorExt (tensor_ext) Dialect includes a series of canonicalization rules that are essential to making automatically generated rotation code efficient:

  • Rotation by zero: rotate %t, 0 folds away to %t

  • Cyclical wraparound: rotate %t, k for $k > t.size$ can be simplified to rotate %t, (k mod t.size)

  • Sequential rotation: %0 = rotate %t, k followed by %1 = rotate %0, l is simplified to rotate %t (k+l)

  • Extraction: %0 = rotate %t, k followed by %1 = tensor.extract %0[l] is simplified to tensor.extract %t[k+l]

  • Binary Arithmetic Ops: where both operands to a binary arith operation are rotations by the same amount, the rotation can be performed only once, on the result. For Example,

    %0 = rotate %t1, k
%1 = rotate %t2, k
%2 = arith.add %0, %1

    can be simplified to

    %0 = arith.add %t1, %t2
%1 = rotate %0, k

  • Sandwiched Binary Arithmetic Ops: If a rotation follows a binary arith operation which has rotation as its operands, the post-arith operation can be moved forward. For example,

    %0 = rotate %t1, x
%1 = rotate %t2, y
%2 = arith.add %0, %1
%3 = rotate %2, z

    can be simplified to

    %0 = rotate %t1, x + z
%1 = rotate %t2, y + z
%2 = arith.add %0, %1

  • Single-Use Arithmetic Ops: Finally, there is a pair of rules that do not eliminate rotations, but move rotations up in the IR, which can help in exposing further canonicalization and/or CSE opportunities. These only apply to arith operations with a single use, as they might otherwise increase the total number of rotations. For example,

    %0 = rotate %t1, k
%2 = arith.add %0, %t2
%1 = rotate %2, l

    can be equivalently rewritten as

    %0 = rotate %t1, (k+l)
%1 = rotate %t2, l
%2 = arith.add %0, %1

    and a similar pattern exists for situations where the rotation is the rhs operand of the arithmetic operation.

Note that the index computations in the patterns above (e.g., k+l, k mod t.size are realized via emitting arith operations. However, for constant/compile-time-known indices, these will be subsequently constant-folded away by the canonicalization pass.

5.7 - Optimizing relinearization

This document outlines the integer linear program model used in the optimize-relinearization pass.

Background

In vector/arithmetic FHE, RLWE ciphertexts often have the form $\mathbf{c} = (c_0, c_1)$, where the details of how $c_0$ and $c_1$ are computed depend on the specific scheme. However, in most of these schemes, the process of decryption can be thought of as taking a dot product between the vector $\mathbf{c}$ and a vector $(1, s)$ containing the secret key $s$ (followed by rounding).

In such schemes, the homomorphic multiplication of two ciphertexts $\mathbf{c} = (c_0, c_1)$ and $\mathbf{d} = (d_0, d_1)$ produces a ciphertext $\mathbf{f} = (f_0, f_1, f_2)$. This triple can be decrypted by taking a dot product with $(1, s, s^2)$.

With this in mind, each RLWE ciphertext $\mathbf{c}$ has an associated key basis, which is the vector $\mathbf{s_c}$ whose dot product with $\mathbf{c}$ decrypts it.

Usually a larger key basis is undesirable. For one, operations in a higher key basis are more expensive and have higher rates of noise growth. Repeated multiplications exponentially increase the length of the key basis. So to avoid this, an operation called relinearization was designed that converts a ciphertext from a given key basis back to $(1, s)$. Doing this requires a set of relinearization keys to be provided by the client and stored by the server.

In general, key bases can be arbitrary. Rotation of an RLWE ciphertext by a shift of $k$, for example, first applies the automorphism $x \mapsto x^k$. This converts the key basis from $(1, s)$ to $(1, s^k)$, and more generally maps $(1, s, s^2, \dots, s^d) \mapsto (1, s^k, s^{2k}, \dots, s^{kd})$. Most FHE implementations post-compose this automorphism with a key switching operation to return to the linear basis $(1, s)$. Similarly, multiplication can be defined for two key bases $(1, s^n)$ and $(1, s^m)$ (with $n < m$) to produce a key basis $(1, s^n, s^m, s^{n+m})$. By a combination of multiplications and rotations (without ever relinearizing or key switching), ciphertexts with a variety of strange key bases can be produced.

Most FHE implementations do not permit wild key bases because each key switch and relinearization operation (for each choice of key basis) requires additional secret key material to be stored by the server. Instead, they often enforce that rotation has key-switching built in, and multiplication relinearizes by default.

That said, many FHE implementations do allow for the relinearization operation to be deferred. A useful such situation is when a series of independent multiplications are performed, and the results are added together. Addition can operate in any key basis (though depending on the backend FHE implementation’s details, all inputs may require the same key basis, cf. Optional operand agreement), and so the relinearization op that follows each multiplication can be deferred until after the additions are complete, at which point there is only one relinearization to perform. This technique is usually called lazy relinearization. It has the benefit of avoiding expensive relinearization operations, as well as reducing noise growth, as relinearization adds noise to the ciphertext, which can further reduce the need for bootstrapping.

In much of the literature, lazy relinearization is applied manually. See for example Blatt-Gusev-Polyakov-Rohloff-Vaikuntanathan 2019 and Lee-Lee-Kim-Kim-No-Kang 2020. In some compiler projects, such as the EVA compiler relinearization is applied automatically via a heuristic, either “eagerly” (immediately after each multiplication op) or “lazily,” deferred as late as possible.

The optimize-relinearization pass

In HEIR, relinearization placement is implemented via a mixed-integer linear program (ILP). It is intended to be more general than a lazy relinearization heuristic, and certain parameter settings of the ILP reproduce lazy relinearization.

The optimize-relinearization pass starts by deleting all relinearization operations from the IR, solves the ILP, and then inserts relinearization ops according to the solution. This implies that the input IR to the ILP has no relinearization ops in it already.

Model specification

The ILP model fits into a family of models that is sometimes called “state-dynamics” models, in that it has “state” variables that track a quantity that flows through a system, as well as “decision” variables that control decisions to change the state at particular points. A brief overview of state dynamics models can be found here

In this ILP, the “state” value is the degree of the key basis. I.e., rather than track the entire key basis, we assume the key basis always has the form $(1, s, s^2, \dots, s^k)$ and track the value $k$. The index tracking state is SSA value, and the decision variables are whether to relinearize.

Variables

Define the following variables:

  • For each operation $o$, $R_o \in { 0, 1 }$ defines the decision to relinearize the result of operation $o$. Relinearization is applied if and only if $R_o = 1$.
  • For each SSA value $v$, $\textup{KB}_v$ is a continuous variable representing the degree of the key basis of $v$. For example, if the key basis of a ciphertext is $(1, s)$, then $\textup{KB}_v = 1$. If $v$ is the result of an operation $o$, $\textup{KB}_v$ is the key basis of the result of $o$ after relinearization has been optionally applied to it, depending on the value of the decision variable $R_o$.
  • For each SSA value $v$ that is an operation result, $\textup{KB}^{br}_v$ is a continuous variable whose value represents the key basis degree of $v$ before relinearization is applied (br = “before relin”). These SSA values are mainly for after the model is solved and relinearization operations need to be inserted into the IR. Here, type conflicts require us to reconstruct the key basis degree, and saving the values allows us to avoid recomputing the values.

Each of the key-basis variables is bounded from above by a parameter MAX_KEY_BASIS_DEGREE that can be used to impose hard limits on the key basis size, which may be required if generating code for a backend that does not support operations over generalized key bases.

Objective

The objective is to minimize the number of relinearization operations, i.e., $\min \sum_o R_o$.

TODO(#1018): update docs when objective is generalized.

Constraints

Simple constraints

The simple constraints are as follows:

  • Initial key basis degree: For each block argument, $\textup{KB}_v$ is fixed to equal the dimension parameter on the RLWE ciphertext type.
  • Special linearized ops: bgv.rotate and func.return require linearized inputs, i.e., $\textup{KB}_{v_i} = 1$ for all inputs $v_i$ to these operations.
  • Before relinearization key basis: for each operation $o$ with operands $v_1, \dots, v_k$, constrain $\textup{KB}^{br}_{\textup{result}(o)} = f(\textup{KB}_{v_1}, \dots, \textup{KB}_{v_k})$, where $f$ is a statically known linear function. For multiplication $f$ it addition, and for all other ops it is the projection onto any input, since multiplication is the only op that increases the degree, and all operands are constrained to have equal degree.

Optional operand agreement

There are two versions of the model, one where the an operation requires the input key basis degrees of each operand to be equal, and one where differing key basis degrees are allowed.

This is an option because the model was originally implemented under the incorrect assumption that CPU backends like OpenFHE and Lattigo require the key basis degree operands to be equal for ops like ciphertext addition. When we discovered this was not the case, we generalized the model to support both cases, in case other backends do have this requirement.

When operands must have the same key basis degree, then for each operation with operand SSA values $v_1, \dots, v_k$, we add the constraint $\textup{KB}_{v_1} = \dots = \textup{KB}_{v_k}$, i.e., all key basis inputs must match.

When operands may have different key basis degrees, we instead add the constraint that each operation result key basis degree (before relinearization) is at least as large as the max of all operand key basis degrees. For all $i$, $\textup{KB}_{\textup{result}(o)}^{br} \geq \textup{KB}_{v_i}$. Note that we are relying on an implicit behavior of the model to ensure that, even if the solver chooses key basis degree variables for these op results larger than the max of the operand degrees, the resulting optimal solution is the same.

TODO(#1018): this will change to a more principled approach when the objective is generalized

Impact of relinearization choices on key basis degree

The remaining constraints control the dynamics of how the key basis degree changes as relinearizations are inserted.

They can be thought of as implementing this (non-linear) constraint for each operation $o$:

\[ \textup{KB}_{\textup{result}(o)} = \begin{cases} \textup{KB}^{br}_{\textup{result(o)}} & \text{ if } R_o = 0 \\ 1 & \text{ if } R_o = 1 \end{cases} \]

Note that $\textup{KB}^{br}_{\textup{result}(o)}$ is constrained by one of the simple constraints to be a linear expression containing key basis variables for the operands of $o$. The conditional above cannot be implemented directly in an ILP. Instead, one can implement it via four constraints that effectively linearize (in the sense of making non-linear constraints linear) the multiplexer formula

\[ \textup{KB}_{\textup{result}(o)} = (1 - R_o) \cdot \textup{KB}^{br}_{\textup{result}(o)} + R_o \cdot 1 \]

(Note the above is not linear because in includes the product of two variables.) The four constraints are:

\[ \begin{aligned} \textup{KB}_\textup{result}(o) &\geq \textup{ R}_o \\ \textup{KB}_\textup{result}(o) &\leq 1 + C(1 – \textup{R}_o) \\ \textup{KB}_\textup{result}(o) &\geq \textup{KB}^{br}_{\textup{result}(o)} – C \textup{ R}_o \\ \textup{KB}_\textup{result}(o) &\leq \textup{KB}^{br}_{\textup{result}(o)} + C \textup{ R}_o \\ \end{aligned} \]

Here $C$ is a constant that can be set to any value larger than MAX_KEY_BASIS_DEGREE. We set it to 100.

Setting $R_o = 0$ makes constraints 1 and 2 trivially satisfied, while constraints 3 and 4 enforce the equality $\textup{KB}_{\textup{result}(o)} = \textup{KB}^{br}_{\textup{result}(o)}$. Likewise, setting $R_o = 1$ makes constraints 3 and 4 trivially satisfied, while constraints 1 and 2 enforce the equality $\textup{KB}_{\textup{result}(o)} = 1$.

Notes

  • ILP performance scales roughly with the number of integer variables. The formulation above only requires the decision variable to be integer, and the initialization and constraints effectively force the key basis variables to be integer. As a result, the solve time of the above ILP should scale with the number of ciphertext-handling ops in the program.

6 - Pipelines

This page documents the pass pipelines available in HEIR for the heir-opt and heir-translate tools.

heir-opt

heir-opt provides several pipelines to lower MLIR programs from standard dialects to FHE dialects.

--heir-simd-vectorizer

Convert FHE programs with naive loops that operate on scalar types to equivalent programs that operate on vectors. This corresponds to the optimizations of the HECO compiler.

This pass is intended to process FHE programs that are known to be good for SIMD, but a specific SIMD-style FHE scheme (BGV, BFV, CKKS) has not yet been chosen. It expects to handle arith ops operating on tensor types (with or without secret.generic).

The pass unrolls all loops, and assumes the input data can be packed in a single ciphertext, interpreted as vectors of slots. For well-structured loops, the resulting SIMD operations can be converted to use minimal ciphertext rotation ops.

--mlir-to-cggi

Converts MLIR IR to the CGGI dialect defined by HEIR. It can either booleanize the IR and optimize the circuit using Yosys optimizations, or convert integer arithmetic to CGGI.

This pipeline has a dataType option, which can be Bool or Integer.

  • When dataType is Bool, the pipeline first bufferizes and applies affine transformations. Then, it uses Yosys to synthesize the logic into a boolean or small-integer arithmetic circuit using comb.truth_table ops to represent programmable bootstrap operations. Finally, it converts the boolean circuit to the CGGI dialect.
  • When dataType is Integer, the pipeline converts arith dialect operations to the CGGI dialect. This is useful for targeting backends that have native support for high-bitwidth FHE arithmetic, such as tfhe-rs.

The pass requires that the environment variable HEIR_ABC_BINARY contains the location of the ABC binary and that HEIR_YOSYS_SCRIPTS_DIR contains the location of the Yosys’ techlib files that are needed to execute the path. This is only needed when dataType is Bool.

--mlir-to-secret-arithmetic

Converts a function using standard MLIR dialects to the secret dialect with arithmetic operations. This pipeline is a precursor to lowering to specific RLWE-based FHE schemes. It performs several transformations:

  • Applies data-oblivious transforms to remove data-dependent control flow.
  • Performs layout optimization to efficiently pack data in ciphertexts.
  • Adds a client interface with helper functions for encryption and decryption.

This pass requires secret func.func inputs to be annotated with the {secret.secret} attribute.

--mlir-to-bgv, --mlir-to-bfv, --mlir-to-ckks

These pipelines convert a function using standard MLIR dialects to a specific RLWE-based FHE scheme: BGV, BFV, or CKKS. They all use the --mlir-to-secret-arithmetic pipeline to perform the initial lowering to secret arithmetic. Then, they perform scheme-specific transformations, including:

  • Inserting and optimizing ciphertext management operations like modulus switching, relinearization, and bootstrapping.
  • Performing scheme-specific parameter generation and noise analysis.
  • Lowering the secret dialect to the target FHE dialect (bgv, bfv, or ckks).

--scheme-to-openfhe

Converts code expressed at the FHE scheme level (BGV, BFV, CKKS) to the openfhe dialect, from which heir-translate can generate C++ code using the OpenFHE library, or else the MLIR can be interpreted using OpenFHE calls.

--scheme-to-lattigo

Converts code expressed at the FHE scheme level (BGV, BFV, CKKS) to the lattigo dialect, from which heir-translate can generate Go code using the Lattigo library.

--scheme-to-tfhe-rs

Converts code expressed in the CGGI dialect to the tfhe_rust dialect, from which heir-translate can generate Rust code using the thfe-rs library.

--scheme-to-fpt

Converts code expressed in the CGGI dialect to the tfhe_rust_bool dialect. This pipeline is used for targeting the FPT and Belfort FPGA mirrors of the tfhe-rs API.

--scheme-to-jaxite

Converts code expressed in the CGGI dialect to the jaxite dialect, from which heir-translate can generate Python code using the Jaxite library.

--torch-linalg-to-ckks

Converts a linalg MLIR program exported from PyTorch to the CKKS FHE scheme. It first applies linalg preprocessing passes and then uses the --mlir-to-ckks pipeline.

--convert-to-data-oblivious

Transforms a program to be data-oblivious by converting control flow on secret data (e.g., if, for, while) into data-independent operations.

--math-to-polynomial-approximation

Approximates math operations that cannot be expressed in FHE using polynomial approximations. This is a sub-pipeline of most other pipelines, exposed for testing purposes.

heir-translate

heir-translate is a tool for translating MLIR dialects to various output formats. heir-translate supports the following emitters:

  • --emit-function-info: Emits function signature information.
  • --emit-jaxite: Emits Python code for the Jaxite TPU library’s CGGI implementation.
  • --emit-jaxiteword: Emits Python code for the Jaxite TPU library’s CKKS implementation.
  • --emit-lattigo: Emits Go code for the Lattigo library.
  • --emit-metadata: Emits a json object describing function signatures.
  • --emit-openfhe-pke-header: Emits a C++ header for the OpenFHE library.
  • --emit-openfhe-pke-pybind: Emits pybind11 bindings for the OpenFHE library.
  • --emit-openfhe-pke: Emits C++ code for the OpenFHE library.
  • --emit-simfhe: Exports code that can be evaluated with the SimFHE simulator.
  • --emit-tfhe-rust-bool: Emits tfhe-rs code against the boolean API.
  • --emit-tfhe-rust-hl: Emits tfhe-rs code against the integer API.
  • --emit-tfhe-rust: Emits tfhe-rs code against the shortint API.
  • --emit-verilog: Emits verilog code for arith and memref programs. Used for integration with Yosys.

7 - Dialects

This section contains the reference documentation for all of the dialects defined in HEIR.

7.1 - BGV

‘bgv’ Dialect

The BGV dialect defines the types and operations of the BGV and B/FV cryptosystem.

Due to similarity with the BFV scheme, BGV dialect also represents the B/FV scheme.

The semantics of bgv dialect operations are determined by the scheme.bgv or scheme.bfv annotation at the module level.

In B/FV mode, bgv.modulus_switch is an no-op.

BGV attributes

SchemeParamAttr

BGV Scheme Parameters

Syntax:

#bgv.scheme_param<
  int,   # logN
  DenseI64ArrayAttr,   # Q
  DenseI64ArrayAttr,   # P
  int64_t,   # plaintextModulus
  BGVEncryptionType,   # encryptionType
  BGVEncryptionTechnique   # encryptionTechnique
>

This attribute is used for recording the scheme parameters for CKKS.

The attribute is a struct with the following fields:

  • int logN: The log of the degree of the polynomial modulus.
  • DenseI64ArrayAttr Q: The array of primes in the ciphertext modulus.
  • DenseI64ArrayAttr P: The array of primes in the special modulus, used for key switching.
  • int64_t plaintextModulus: The plaintext modulus.

Parameters:

ParameterC++ typeDescription
logNint
QDenseI64ArrayAttr
PDenseI64ArrayAttr
plaintextModulusint64_t
encryptionTypeBGVEncryptionType
encryptionTechniqueBGVEncryptionTechnique

BGV ops

bgv.add (heir::bgv::AddOp)

Addition operation between ciphertexts.

Syntax:

operation ::= `bgv.add` operands attr-dict `:`  functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultPlaintextTypes, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.add_plain (heir::bgv::AddPlainOp)

Addition operation between ciphertext-plaintext.

Syntax:

operation ::= `bgv.add_plain` operands attr-dict `:`  functional-type(operands, results)

Traits: AllCiphertextTypesMatch, AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, IsCiphertextPlaintextOp, SameOperandsAndResultPlaintextTypes, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.level_reduce (heir::bgv::LevelReduceOp)

Lower the modulus level of the ciphertext via dropping RNS limbs.

Syntax:

operation ::= `bgv.level_reduce` operands attr-dict `:` qualified(type($input)) `->` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultPlaintextTypes, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
levelToDrop::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.modulus_switch (heir::bgv::ModulusSwitchOp)

Lower the modulus level of the ciphertext via modulus switching.

Syntax:

operation ::= `bgv.modulus_switch` operands attr-dict `:` qualified(type($input)) `->` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
to_ring::mlir::heir::polynomial::RingAttran attribute specifying a polynomial ring

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.mul (heir::bgv::MulOp)

Multiplication operation between ciphertexts.

Syntax:

operation ::= `bgv.mul` operands attr-dict `:`  functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.mul_plain (heir::bgv::MulPlainOp)

Multiplication operation between ciphertext-plaintext.

Syntax:

operation ::= `bgv.mul_plain` operands attr-dict `:`  functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, IsCiphertextPlaintextOp, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.negate (heir::bgv::NegateOp)

Negate the coefficients of the ciphertext.

Syntax:

operation ::= `bgv.negate` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Elementwise, Involution, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.relinearize (heir::bgv::RelinearizeOp)

Relinearize the ciphertext.

Syntax:

operation ::= `bgv.relinearize` operands attr-dict `:` qualified(type($input)) `->` qualified(type($output))

This op takes integer array attributes from_basis and to_basis that are used to indicate the key basis from which and to which the ciphertext is encrypted against. A ciphertext is canonically encrypted against key basis (1, s). After a multiplication, its size will increase and the basis will be (1, s, s^2). The array that represents the key basis is constructed by listing the powers of s at each position of the array. For example, (1, s, s^2) corresponds to [0, 1, 2], while (1, s^2) corresponds to [0, 2].

Traits: AlwaysSpeculatableImplTrait, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultPlaintextTypes, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
from_basis::mlir::DenseI32ArrayAttri32 dense array attribute
to_basis::mlir::DenseI32ArrayAttri32 dense array attribute

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.rotate_cols (heir::bgv::RotateColumnsOp)

Rotate the columns of the coefficients of the ciphertext using a Galois automorphism.

Syntax:

operation ::= `bgv.rotate_cols` operands attr-dict `:` qualified(type($input))

This operation rotates the columns of the coefficients of the ciphertext using a Galois automorphism.

Often BGV scheme is instantiated with a ring of the form Z_q[X]/(X^N + 1) and plaintext modulus t where N is a power of 2 and t is a prime number. In this case, the plaintext slots can be viewed as a 2 x N/2 matrix where N/2 is the number of columns and 2 is the number of rows.

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
offset::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.rotate_rows (heir::bgv::RotateRowsOp)

Rotate the rows of the coefficients of the ciphertext using a Galois automorphism.

Syntax:

operation ::= `bgv.rotate_rows` operands attr-dict `:` qualified(type($input))

This operation rotates the rows of the coefficients of the ciphertext using a Galois automorphism.

Often BGV scheme is instantiated with a ring of the form Z_q[X]/(X^N + 1) and plaintext modulus t where N is a power of 2 and t is a prime number. In this case, the plaintext slots can be viewed as a 2 x N/2 matrix where N/2 is the number of columns and 2 is the number of rows.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
offset::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.sub (heir::bgv::SubOp)

Subtraction operation between ciphertexts.

Syntax:

operation ::= `bgv.sub` operands attr-dict `:`  functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultPlaintextTypes, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

bgv.sub_plain (heir::bgv::SubPlainOp)

Subtraction operation between ciphertext-plaintext.

Syntax:

operation ::= `bgv.sub_plain` operands attr-dict `:`  functional-type(operands, results)

Traits: AllCiphertextTypesMatch, AlwaysSpeculatableImplTrait, Elementwise, InferTypeOpAdaptor, IsCiphertextPlaintextOp, SameOperandsAndResultPlaintextTypes, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

BGV additional definitions

BGVEncryptionTechnique

An enum attribute representing an encryption technique

Cases:

SymbolValueString
standard0standard
extended1extended

BGVEncryptionType

An enum attribute representing an encryption method

Cases:

SymbolValueString
pk0pk
sk1sk

7.2 - CGGI

‘cggi’ Dialect

A dialect for types and operations in the CGGI cryptosystem

CGGI attributes

CGGIBoolGatesAttr

An attribute containing an array of strings to store bool gates

Syntax:

#cggi.cggi_bool_gates<
  ::llvm::ArrayRef<::mlir::heir::cggi::CGGIBoolGateEnumAttr>   # gates
>

This attributes stores a list of integer identifiers for Boolean gates.

Uses following mapping: AND_GATE = 0; NAND_GATE = 1; OR_GATE = 2; NOR_GATE = 3; XOR_GATE = 4; XNOR_GATE = 5; NOT_GATE = 6;

Parameters:

ParameterC++ typeDescription
gates::llvm::ArrayRef<::mlir::heir::cggi::CGGIBoolGateEnumAttr>

CGGI ops

cggi.add (heir::cggi::AddOp)

Arithmetic addition of two ciphertexts. One of the two ciphertext is allowed to be a scalar, this will result in the scalar addition to a ciphertext.

Syntax:

operation ::= `cggi.add` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsA ciphertext type
rhsInteger type with arbitrary precision up to a fixed limit or A ciphertext type

Results:

ResultDescription
outputA ciphertext type

cggi.and (heir::cggi::AndOp)

Logical AND of two ciphertexts.

Syntax:

operation ::= `cggi.and` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.cast (heir::cggi::CastOp)

Change the plaintext space of a CGGI ciphertext

Syntax:

operation ::= `cggi.cast` $input attr-dict `:` type($input) `to` type($output)

“cast” operation to change the plaintext size of a CGGI ciphertext. Note this operations is not a standard CGGI operation, but an mirror of the cast op implemented in TFHE-rs.

Examples:

`cggi.cast %c0 : !lwe.lwe_ciphertext<encoding = #unspecified_bit_field_encoding> to !lwe.lwe_ciphertext<encoding = #unspecified_bit_field_encoding1>`

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultShape

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.cmp (heir::cggi::CmpOp)

_High level operation to check the relation of two ciphertexts.

  • equal (mnemonic: “eq”; integer value: 0)
  • not equal (mnemonic: “ne”; integer value: 1)
  • signed less than (mnemonic: “slt”; integer value: 2)
  • signed less than or equal (mnemonic: “sle”; integer value: 3)
  • signed greater than (mnemonic: “sgt”; integer value: 4)
  • signed greater than or equal (mnemonic: “sge”; integer value: 5)
  • unsigned less than (mnemonic: “ult”; integer value: 6)
  • unsigned less than or equal (mnemonic: “ule”; integer value: 7)
  • unsigned greater than (mnemonic: “ugt”; integer value: 8)
  • unsigned greater than or equal (mnemonic: “uge”; integer value: 9)

Note: https://mlir.llvm.org/docs/Dialects/ArithOps/#arithcmpi-arithcmpiop Note this operations to indirect mirror the TFHE-rs implmementation._

Syntax:

operation ::= `cggi.cmp` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
predicate::mlir::arith::CmpIPredicateAttrallowed 64-bit signless integer cases: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Operands:

OperandDescription
lhslwe-ciphertext-like
rhsInteger type with arbitrary precision up to a fixed limit or lwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.create_trivial (heir::cggi::CreateTrivialOp)

Syntax:

operation ::= `cggi.create_trivial` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
value::mlir::AttributeAn Attribute containing a integer value or A collection of other Attribute values

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.eq (heir::cggi::EqOp)

High level operation to check equality of two ciphertexts. Note this operations to mirror the TFHE-rs implmementation.

Syntax:

operation ::= `cggi.eq` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsA ciphertext type
rhsInteger type with arbitrary precision up to a fixed limit or A ciphertext type

Results:

ResultDescription
outputA ciphertext type

cggi.lut2 (heir::cggi::Lut2Op)

A lookup table on two inputs.

Syntax:

operation ::= `cggi.lut2` operands attr-dict `:` qualified(type($output))

An op representing a lookup table applied to some number n of ciphertexts encrypting boolean input bits.

Over cleartext bits a, b, c, using n = 3 for example, the operation computed by this function can be interpreted as

  truth_table >> {c, b, a}

where {c, b, a} is the unsigned 3-bit integer with bits c, b, a from most significant bit to least-significant bit. The input are combined into a single ciphertext input to the lookup table using products with plaintexts and sums.

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, LUTOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
lookup_table::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
blwe-ciphertext-like
alwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.lut3 (heir::cggi::Lut3Op)

A lookup table on three inputs.

Syntax:

operation ::= `cggi.lut3` operands attr-dict `:` qualified(type($output))

An op representing a lookup table applied to some number n of ciphertexts encrypting boolean input bits.

Over cleartext bits a, b, c, using n = 3 for example, the operation computed by this function can be interpreted as

  truth_table >> {c, b, a}

where {c, b, a} is the unsigned 3-bit integer with bits c, b, a from most significant bit to least-significant bit. The input are combined into a single ciphertext input to the lookup table using products with plaintexts and sums.

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, LUTOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
lookup_table::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
clwe-ciphertext-like
blwe-ciphertext-like
alwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.lut_lincomb (heir::cggi::LutLinCombOp)

A variadic-input lookup table with inputs prepared via linear combination.

Syntax:

operation ::= `cggi.lut_lincomb` operands attr-dict `:` type($output)

An op representing a lookup table applied to an arbitrary number of input ciphertexts, which are combined according to a static linear combination attached to the op.

The user must ensure the chosen linear combination does not bleed error bits into the message space according to the underlying ciphertext’s encoding attributes. E.g., a bit_field_encoding with 3 cleartext bits cannot be multiplied by 16.

Example:

#encoding = #lwe.bit_field_encoding<cleartext_start=30, cleartext_bitwidth=3>
#params = #lwe.lwe_params<cmod=7917, dimension=4>
!ciphertext = !lwe.lwe_ciphertext<encoding = #encoding, lwe_params = #params>

%4 = cggi.lut_lincomb %c0, %c1, %c2, %c3 {coefficients = array<i32: 1, 2, 3, 2>, lookup_table = 68 : index} : !ciphertext

Represents applying the lut

  68 >> (1 * c0 + 2 * c1 + 3 * c2 + 2 * c3)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, LUTOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
coefficients::mlir::DenseI32ArrayAttri32 dense array attribute
lookup_table::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
inputsvariadic of any type

Results:

ResultDescription
outputany type

cggi.max (heir::cggi::MaxOp)

High level operation to return maximum of two ciphertexts. Note this operations to mirror the TFHE-rs implmementation.

Syntax:

operation ::= `cggi.max` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsA ciphertext type
rhsInteger type with arbitrary precision up to a fixed limit or A ciphertext type

Results:

ResultDescription
outputA ciphertext type

cggi.min (heir::cggi::MinOp)

High level operation to return minimum of two ciphertexts. Note this operations to mirror the TFHE-rs implmementation.

Syntax:

operation ::= `cggi.min` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsA ciphertext type
rhsInteger type with arbitrary precision up to a fixed limit or A ciphertext type

Results:

ResultDescription
outputA ciphertext type

cggi.mul (heir::cggi::MulOp)

Arithmetic multiplication of two ciphertexts. One of the two ciphertext is allowed to be a scalar, this will result in the scalar multiplication to a ciphertext.

Syntax:

operation ::= `cggi.mul` operands attr-dict `:` functional-type(operands, results)

While CGGI does not have a native multiplication operation, some backend targets provide a multiplication operation that is implemented via a sequence of other atomic CGGI ops. When lowering to backends that do not have this, one must lower to this op the appropriate CGGI ops.

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsA ciphertext type
rhsInteger type with arbitrary precision up to a fixed limit or A ciphertext type

Results:

ResultDescription
outputA ciphertext type

cggi.multi_lut_lincomb (heir::cggi::MultiLutLinCombOp)

A multi-output version of lut_lincomb with one LUT per output.

Syntax:

operation ::= `cggi.multi_lut_lincomb` operands attr-dict `:` functional-type($inputs, $outputs)

An op representing multiple lookup tables applied to a shared input, which is prepared via a static linear combination. This is equivalent to cggi.lut_lincomb, but where the linear combination is given to multiple lookup tables, each producing a separate output.

Example:

#encoding = #lwe.bit_field_encoding<cleartext_start=30, cleartext_bitwidth=3>
#params = #lwe.lwe_params<cmod=7917, dimension=4>
!ciphertext = !lwe.lwe_ciphertext<encoding = #encoding, lwe_params = #params>

%4 = cggi.multi_lut_lincomb %c0, %c1, %c2, %c3 {
    coefficients = array<i8: 1, 2, 3, 2>,
    lookup_tables = array<index: 68, 70, 4, 8>
} : (!ciphertext, !ciphertext, !ciphertext, !ciphertext) -> (!ciphertext, !ciphertext, !ciphertext, !ciphertext)

Represents applying the following LUTs. Performance-wise, this is comparable to applying a single LUT to a linear combination.

x = (1 * c0 + 2 * c1 + 3 * c2 + 2 * c3)
return (
  (68 >> x) & 1,
  (70 >> x) & 1,
  (4 >> x) & 1,
  (8 >> x) & 1
)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
coefficients::mlir::DenseI32ArrayAttri32 dense array attribute
lookup_tables::mlir::DenseI32ArrayAttri32 dense array attribute

Operands:

OperandDescription
inputsvariadic of lwe-ciphertext-like

Results:

ResultDescription
outputsvariadic of lwe-ciphertext-like

cggi.nand (heir::cggi::NandOp)

Logical NAND of two ciphertexts.

Syntax:

operation ::= `cggi.nand` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.neq (heir::cggi::NeqOp)

High level operation to check inequality of two ciphertexts. Note this operations to mirror the TFHE-rs implmementation.

Syntax:

operation ::= `cggi.neq` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsA ciphertext type
rhsInteger type with arbitrary precision up to a fixed limit or A ciphertext type

Results:

ResultDescription
outputA ciphertext type

cggi.nor (heir::cggi::NorOp)

Logical NOR of two ciphertexts.

Syntax:

operation ::= `cggi.nor` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.not (heir::cggi::NotOp)

Logical NOT of two ciphertexts

Syntax:

operation ::= `cggi.not` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Elementwise, Involution, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.or (heir::cggi::OrOp)

Logical OR of two ciphertexts.

Syntax:

operation ::= `cggi.or` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.packed_lut3 (heir::cggi::PackedLut3Op)

Syntax:

operation ::= `cggi.packed_lut3` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, LUTOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
lookup_tables::mlir::ArrayAttrArray of integers

Operands:

OperandDescription
alwe-ciphertext-like
blwe-ciphertext-like
clwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.packed_gates (heir::cggi::PackedOp)

Syntax:

operation ::= `cggi.packed_gates` operands attr-dict `:` functional-type(operands, results)

Operation to where different Boolean gates are executed pairwise between elements of two ciphertext arrays.

For example,

%0 = cggi.packed_gates %a, %b {gates = #cggi.cggi_gate<"and", "xor">} : tensor<2x!lwe.lwe_ciphertext>

applies an “and” gate to the first elements of %a and %b and an xor gate to the second elements.

Mapping is defined in the BooleanGates.td file.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
gates::mlir::heir::cggi::CGGIBoolGatesAttrAn attribute containing an array of strings to store bool gates

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.programmable_bootstrap (heir::cggi::ProgrammableBootstrapOp)

Programmable Bootstrap with a given lookup table.

Syntax:

operation ::= `cggi.programmable_bootstrap` operands attr-dict `:` qualified(type($output))

An op representing a programmable bootstrap applied to an LWE ciphertext.

This operation evaluates a univariate function homomorphically on the ciphertext by selecting the correct value from a lookup table. The bit size of the lookup table integer attribute should be equal to the plaintext space size. For example, if there ciphertext can hold 3 plaintext message bits, then the lookup table must be represented at most by an integer with 8 bits.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
lookup_table::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.sshl (heir::cggi::ScalarShiftLeftOp)

Arithmetic shift to left of a ciphertext by an integer. Note this operations to mirror the TFHE-rs implmementation.

Syntax:

operation ::= `cggi.sshl` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
shiftAmount::mlir::IntegerAttrindex attribute

Operands:

OperandDescription
lhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.sshr (heir::cggi::ScalarShiftRightOp)

Arithmetic shift to the right of a ciphertext by an integer. Note this operations to mirror the TFHE-rs implmementation.

Syntax:

operation ::= `cggi.sshr` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
shiftAmount::mlir::IntegerAttrindex attribute

Operands:

OperandDescription
lhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.cmux (heir::cggi::SelectOp)

Multiplexer operations, the select ciphertext will return the trueCtxt if in contains a 1. In the other case, it will will return the falseCtxt. Note this operations to mirror the TFHE-rs implmementation."

Syntax:

operation ::= `cggi.cmux` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
selectlwe-ciphertext-like
trueCtxtlwe-ciphertext-like
falseCtxtlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.selector_lut_lincomb (heir::cggi::SelectorLutLinCombOp)

A multi-value version of lut_lincomb

Syntax:

operation ::= `cggi.selector_lut_lincomb` operands attr-dict `:` functional-type($inputs, $outputs)

An op representing a lookup table applied to a shared input, which is prepared via a static linear combination. This is equivalent to cggi.lut_lincomb, but where the linear combination is given to a single LUT, but producing an single n-bit output.

The linear combination will select a value for a lookup table with 2^n outputs where each output is a n-bit number. For instance, in the case of the default i4 ciphertext, a 16 element lookup table will be used, and the output will be a i4 number.

Example:

#encoding = #lwe.bit_field_encoding<cleartext_start=30, cleartext_bitwidth=3>
#params = #lwe.lwe_params<cmod=7917, dimension=4>
!ciphertext = !lwe.lwe_ciphertext<encoding = #encoding, lwe_params = #params>

%4 = cggi.selector_lut_lincomb %c0, %c1 {
    coefficients = array<i8: 1, 2>,
    lookup_tables = array<i8: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15>
} : (!ciphertext, !ciphertext) -> (!ciphertext)

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
coefficients::mlir::DenseI8ArrayAttri8 dense array attribute
lookup_tables::mlir::DenseI8ArrayAttri8 dense array attribute

Operands:

OperandDescription
inputsvariadic of lwe-ciphertext-like

Results:

ResultDescription
outputslwe-ciphertext-like

cggi.sub (heir::cggi::SubOp)

Subtraction of two ciphertexts.

Syntax:

operation ::= `cggi.sub` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsA ciphertext type
rhsInteger type with arbitrary precision up to a fixed limit or A ciphertext type

Results:

ResultDescription
outputA ciphertext type

cggi.xnor (heir::cggi::XNorOp)

Logical XNOR of two ciphertexts.

Syntax:

operation ::= `cggi.xnor` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

cggi.xor (heir::cggi::XorOp)

Logical XOR of two ciphertexts.

Syntax:

operation ::= `cggi.xor` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

CGGI additional definitions

CGGIBoolGateEnum

An enum attribute representing a CGGI boolean gate using u8 int

Cases:

SymbolValueString
AND0AND
NAND1NAND
OR2OR
NOR3NOR
XOR4XOR
XNOR5XNOR
NOT6NOT

7.3 - CKKS

‘ckks’ Dialect

The CKKS dialect defines the types and operations of the CKKS cryptosystem.

CKKS attributes

SchemeParamAttr

CKKS Scheme Parameters

Syntax:

#ckks.scheme_param<
  int,   # logN
  DenseI64ArrayAttr,   # Q
  DenseI64ArrayAttr,   # P
  int,   # logDefaultScale
  CKKSEncryptionType,   # encryptionType
  CKKSEncryptionTechnique   # encryptionTechnique
>

This attribute is used for recording the scheme parameters for CKKS.

The attribute is a struct with the following fields:

  • int logN: The log of the degree of the polynomial modulus.
  • DenseI64ArrayAttr Q: The array of primes in the ciphertext modulus.
  • DenseI64ArrayAttr P: The array of primes in the special modulus, used for key switching.
  • int logDefaultScale: The log of the default scale.

Parameters:

ParameterC++ typeDescription
logNint
QDenseI64ArrayAttr
PDenseI64ArrayAttr
logDefaultScaleint
encryptionTypeCKKSEncryptionType
encryptionTechniqueCKKSEncryptionTechnique

CKKS ops

ckks.add (heir::ckks::AddOp)

Addition operation between ciphertexts.

Syntax:

operation ::= `ckks.add` operands attr-dict `:`  functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultPlaintextTypes, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.add_plain (heir::ckks::AddPlainOp)

Addition operation between ciphertext-plaintext.

Syntax:

operation ::= `ckks.add_plain` operands attr-dict `:`  functional-type(operands, results)

Traits: AllCiphertextTypesMatch, AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, IsCiphertextPlaintextOp, SameOperandsAndResultPlaintextTypes, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.bootstrap (heir::ckks::BootstrapOp)

Bootstrap the ciphertext to reduce noise and refresh its parameters.

Syntax:

operation ::= `ckks.bootstrap` operands attr-dict `:` qualified(type($input)) `->` qualified(type($output))

Bootstrapping is a technique used in FHE to reduce the noise in a ciphertext and refresh its parameters, allowing for further computations on the ciphertext.

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.level_reduce (heir::ckks::LevelReduceOp)

Lower the modulus level of the ciphertext via dropping RNS limbs.

Syntax:

operation ::= `ckks.level_reduce` operands attr-dict `:` qualified(type($input)) `->` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultPlaintextTypes, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
levelToDrop::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.mul (heir::ckks::MulOp)

Multiplication operation between ciphertexts.

Syntax:

operation ::= `ckks.mul` operands attr-dict `:`  functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.mul_plain (heir::ckks::MulPlainOp)

Multiplication operation between ciphertext-plaintext.

Syntax:

operation ::= `ckks.mul_plain` operands attr-dict `:`  functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, IsCiphertextPlaintextOp, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.negate (heir::ckks::NegateOp)

Negate the coefficients of the ciphertext.

Syntax:

operation ::= `ckks.negate` operands attr-dict `:` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Elementwise, Involution, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.relinearize (heir::ckks::RelinearizeOp)

Relinearize the ciphertext.

Syntax:

operation ::= `ckks.relinearize` $input (`,` $keySwitchingKey^)? attr-dict `:` functional-type(operands, results)

This op takes integer array attributes from_basis and to_basis that are used to indicate the key basis from which and to which the ciphertext is encrypted against. A ciphertext is canonically encrypted against key basis (1, s). After a multiplication, its size will increase and the basis will be (1, s, s^2). The array that represents the key basis is constructed by listing the powers of s at each position of the array. For example, (1, s, s^2) corresponds to [0, 1, 2], while (1, s^2) corresponds to [0, 2].

Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor, SameOperandsAndResultPlaintextTypes, SameOperandsAndResultRings

Interfaces: ConditionallySpeculatable, ElementwiseByOperandOpInterface, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
from_basis::mlir::DenseI32ArrayAttri32 dense array attribute
to_basis::mlir::DenseI32ArrayAttri32 dense array attribute

Operands:

OperandDescription
inputlwe-ciphertext-like
keySwitchingKeyranked tensor of lwe-ciphertext-like values

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.rescale (heir::ckks::RescaleOp)

Rescales the ciphertext, which is the CKKS version of modulus switching in BGV/BFV.

Syntax:

operation ::= `ckks.rescale` operands attr-dict `:` qualified(type($input)) `->` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
to_ring::mlir::heir::polynomial::RingAttran attribute specifying a polynomial ring

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.rotate (heir::ckks::RotateOp)

Rotate the coefficients of the ciphertext using a Galois automorphism.

Syntax:

operation ::= `ckks.rotate` operands attr-dict `:` qualified(type($input))

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
offset::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.sub (heir::ckks::SubOp)

Subtraction operation between ciphertexts.

Syntax:

operation ::= `ckks.sub` operands attr-dict `:`  functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultPlaintextTypes, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

ckks.sub_plain (heir::ckks::SubPlainOp)

Subtraction operation between ciphertext-plaintext.

Syntax:

operation ::= `ckks.sub_plain` operands attr-dict `:`  functional-type(operands, results)

Traits: AllCiphertextTypesMatch, AlwaysSpeculatableImplTrait, Elementwise, InferTypeOpAdaptor, IsCiphertextPlaintextOp, SameOperandsAndResultPlaintextTypes, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

CKKS additional definitions

CKKSEncryptionTechnique

An enum attribute representing an encryption technique

Cases:

SymbolValueString
standard0standard
extended1extended

CKKSEncryptionType

An enum attribute representing an encryption method

Cases:

SymbolValueString
pk0pk
sk1sk

7.4 - Comb

‘comb’ Dialect

Types and operations for comb dialect

This dialect defines the comb dialect, which is intended to be a generic representation of combinational logic outside of a particular use-case.

Operations

comb.add (heir::comb::AddOp)

Syntax:

operation ::= `comb.add` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.and (heir::comb::AndOp)

Syntax:

operation ::= `comb.and` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.concat (heir::comb::ConcatOp)

Concatenate a variadic list of operands together.

Syntax:

operation ::= `comb.concat` $inputs attr-dict `:` qualified(type($inputs))

See the comb rationale document for details on operand ordering.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.extract (heir::comb::ExtractOp)

Extract a range of bits into a smaller value, lowBit specifies the lowest bit included.

Syntax:

operation ::= `comb.extract` $input `from` $lowBit attr-dict `:` functional-type($input, $result)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
lowBit::mlir::IntegerAttr32-bit signless integer attribute

Operands:

OperandDescription
inputsignless integer

Results:

ResultDescription
resultsignless integer

comb.icmp (heir::comb::ICmpOp)

Compare two integer values

Syntax:

operation ::= `comb.icmp` (`bin` $twoState^)? $predicate $lhs `,` $rhs attr-dict `:` qualified(type($lhs))

This operation compares two integers using a predicate. If the predicate is true, returns 1, otherwise returns 0. This operation always returns a one bit wide result.

    %r = comb.icmp eq %a, %b : i4

Traits: AlwaysSpeculatableImplTrait, SameTypeOperands

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
predicate::mlir::heir::comb::ICmpPredicateAttrhw.icmp comparison predicate
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
lhssignless integer
rhssignless integer

Results:

ResultDescription
result1-bit signless integer

comb.inv (heir::comb::InvOp)

Syntax:

operation ::= `comb.inv` (`bin` $twoState^)? $input attr-dict `:` qualified(type($input))

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsignless integer

Results:

ResultDescription
resultsignless integer

comb.lut (heir::comb::LUTOp)

Return an integer based on a lookup table

Syntax:

operation ::= `comb.lut` operands attr-dict `:` functional-type(operands, results)

This operation is similar to truth_table, but it allows for an integer output instead of a boolean. Requers an vector of integers as the lookup table, where each integer represents the output for a specific combination of inputs.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
coefficients::mlir::DenseI8ArrayAttri8 dense array attribute
lookupTable::mlir::DenseI8ArrayAttri8 dense array attribute

Operands:

OperandDescription
inputsvariadic of 8-bit signless integer

Results:

ResultDescription
result8-bit signless integer

comb.mul (heir::comb::MulOp)

Syntax:

operation ::= `comb.mul` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.mux (heir::comb::MuxOp)

Return one or the other operand depending on a selector bit

Syntax:

operation ::= `comb.mux` (`bin` $twoState^)? $cond `,` $trueValue `,` $falseValue  attr-dict `:` qualified(type($result))

  %0 = mux %pred, %tvalue, %fvalue : i4

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
cond1-bit signless integer
trueValueany type
falseValueany type

Results:

ResultDescription
resultany type

comb.nand (heir::comb::NandOp)

Syntax:

operation ::= `comb.nand` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.nor (heir::comb::NorOp)

Syntax:

operation ::= `comb.nor` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.or (heir::comb::OrOp)

Syntax:

operation ::= `comb.or` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.parity (heir::comb::ParityOp)

Syntax:

operation ::= `comb.parity` (`bin` $twoState^)? $input attr-dict `:` qualified(type($input))

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsignless integer

Results:

ResultDescription
result1-bit signless integer

comb.replicate (heir::comb::ReplicateOp)

Concatenate the operand a constant number of times

Syntax:

operation ::= `comb.replicate` $input attr-dict `:` functional-type($input, $result)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputsignless integer

Results:

ResultDescription
resultsignless integer

comb.truth_table (heir::comb::TruthTableOp)

Return a true/false based on a lookup table

Syntax:

operation ::= `comb.truth_table` $inputs `->` $lookupTable attr-dict

  %a = ... : i1
  %b = ... : i1
  %0 = comb.truth_table %a, %b -> 6 : ui4

This operation assumes that the lookup table is described as an integer of 2^n bits to fully specify the table. Inputs are sorted MSB -> LSB from left to right and the offset into lookupTable is computed from them. The integer containing the truth table value’s LSB is the output for the input “all false”, and the MSB is the output for the input “all true”.

No difference from array_get into an array of constants except for xprop behavior. If one of the inputs is unknown, but said input doesn’t make a difference in the output (based on the lookup table) the result should not be ‘x’ – it should be the well-known result.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, LUTOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
lookupTable::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
inputsvariadic of 1-bit signless integer

Results:

ResultDescription
result1-bit signless integer

comb.xnor (heir::comb::XNorOp)

Syntax:

operation ::= `comb.xnor` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.xor (heir::comb::XorOp)

Syntax:

operation ::= `comb.xor` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

Enums

ICmpPredicate

Hw.icmp comparison predicate

Cases:

SymbolValueString
eq0eq
ne1ne
slt2slt
sle3sle
sgt4sgt
sge5sge
ult6ult
ule7ule
ugt8ugt
uge9uge
ceq10ceq
cne11cne
weq12weq
wne13wne

Comb types

BFloat16Type

Bfloat16 floating-point type

ComplexType

Complex number with a parameterized element type

Syntax:

complex-type ::= `complex` `<` type `>`

The value of complex type represents a complex number with a parameterized element type, which is composed of a real and imaginary value of that element type. The element must be a floating point or integer scalar type.

Example:

complex<f32>
complex<i32>

Parameters:

ParameterC++ typeDescription
elementTypeType

Float4E2M1FNType

4-bit floating point with 2-bit exponent and 1-bit mantissa

An 4-bit floating point type with 1 sign bit, 2 bits exponent and 1 bit mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions with the following characteristics:

  • bit encoding: S1E2M1
  • exponent bias: 1
  • infinities: Not supported
  • NaNs: Not supported
  • denormals when exponent is 0

Open Compute Project (OCP) microscaling formats (MX) specification: https://www.opencompute.org/documents/ocp-microscaling-formats-mx-v1-0-spec-final-pdf

Float6E2M3FNType

6-bit floating point with 2-bit exponent and 3-bit mantissa

An 6-bit floating point type with 1 sign bit, 2 bits exponent and 3 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions with the following characteristics:

  • bit encoding: S1E2M3
  • exponent bias: 1
  • infinities: Not supported
  • NaNs: Not supported
  • denormals when exponent is 0

Open Compute Project (OCP) microscaling formats (MX) specification: https://www.opencompute.org/documents/ocp-microscaling-formats-mx-v1-0-spec-final-pdf

Float6E3M2FNType

6-bit floating point with 3-bit exponent and 2-bit mantissa

An 6-bit floating point type with 1 sign bit, 3 bits exponent and 2 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions with the following characteristics:

  • bit encoding: S1E3M2
  • exponent bias: 3
  • infinities: Not supported
  • NaNs: Not supported
  • denormals when exponent is 0

Open Compute Project (OCP) microscaling formats (MX) specification: https://www.opencompute.org/documents/ocp-microscaling-formats-mx-v1-0-spec-final-pdf

Float8E3M4Type

8-bit floating point with 3 bits exponent and 4 bit mantissa

An 8-bit floating point type with 1 sign bit, 3 bits exponent and 4 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions with the following characteristics:

  • bit encoding: S1E3M4
  • exponent bias: 3
  • infinities: supported with exponent set to all 1s and mantissa 0s
  • NaNs: supported with exponent bits set to all 1s and mantissa values of {0,1}⁴ except S.111.0000
  • denormals when exponent is 0

Float8E4M3Type

8-bit floating point with 3 bit mantissa

An 8-bit floating point type with 1 sign bit, 4 bits exponent and 3 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions with the following characteristics:

  • bit encoding: S1E4M3
  • exponent bias: 7
  • infinities: supported with exponent set to all 1s and mantissa 0s
  • NaNs: supported with exponent bits set to all 1s and mantissa of (001, 010, 011, 100, 101, 110, 111)
  • denormals when exponent is 0

Float8E4M3B11FNUZType

8-bit floating point with 3 bit mantissa

An 8-bit floating point type with 1 sign bit, 4 bits exponent and 3 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions, with the exception that there are no infinity values, no negative zero, and only one NaN representation. This type has the following characteristics:

  • bit encoding: S1E4M3
  • exponent bias: 11
  • infinities: Not supported
  • NaNs: Supported with sign bit set to 1, exponent bits and mantissa bits set to all 0s
  • denormals when exponent is 0

Related to: https://dl.acm.org/doi/10.5555/3454287.3454728

Float8E4M3FNType

8-bit floating point with 3 bit mantissa

An 8-bit floating point type with 1 sign bit, 4 bits exponent and 3 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions, with the exception that there are no infinity values and only two NaN representations. This type has the following characteristics:

  • bit encoding: S1E4M3
  • exponent bias: 7
  • infinities: Not supported
  • NaNs: supported with exponent bits and mantissa bits set to all 1s
  • denormals when exponent is 0

Described in: https://arxiv.org/abs/2209.05433

Float8E4M3FNUZType

8-bit floating point with 3 bit mantissa

An 8-bit floating point type with 1 sign bit, 4 bits exponent and 3 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions, with the exception that there are no infinity values, no negative zero, and only one NaN representation. This type has the following characteristics:

  • bit encoding: S1E4M3
  • exponent bias: 8
  • infinities: Not supported
  • NaNs: Supported with sign bit set to 1, exponent bits and mantissa bits set to all 0s
  • denormals when exponent is 0

Described in: https://arxiv.org/abs/2209.05433

Float8E5M2Type

8-bit floating point with 2 bit mantissa

An 8-bit floating point type with 1 sign bit, 5 bits exponent and 2 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions with the following characteristics:

  • bit encoding: S1E5M2
  • exponent bias: 15
  • infinities: supported with exponent set to all 1s and mantissa 0s
  • NaNs: supported with exponent bits set to all 1s and mantissa of (01, 10, or 11)
  • denormals when exponent is 0

Described in: https://arxiv.org/abs/2209.05433

Float8E5M2FNUZType

8-bit floating point with 2 bit mantissa

An 8-bit floating point type with 1 sign bit, 5 bits exponent and 2 bits mantissa. This is not a standard type as defined by IEEE-754, but it follows similar conventions, with the exception that there are no infinity values, no negative zero, and only one NaN representation. This type has the following characteristics:

  • bit encoding: S1E5M2
  • exponent bias: 16
  • infinities: Not supported
  • NaNs: Supported with sign bit set to 1, exponent bits and mantissa bits set to all 0s
  • denormals when exponent is 0

Described in: https://arxiv.org/abs/2206.02915

Float8E8M0FNUType

8-bit floating point with 8-bit exponent, no mantissa or sign

An 8-bit floating point type with no sign bit, 8 bits exponent and no mantissa. This is not a standard type as defined by IEEE-754; it is intended to be used for representing scaling factors, so it cannot represent zeros and negative numbers. The values it can represent are powers of two in the range [-127,127] and NaN.

  • bit encoding: S0E8M0
  • exponent bias: 127
  • infinities: Not supported
  • NaNs: Supported with all bits set to 1
  • denormals: Not supported

Open Compute Project (OCP) microscaling formats (MX) specification: https://www.opencompute.org/documents/ocp-microscaling-formats-mx-v1-0-spec-final-pdf

Float16Type

16-bit floating-point type

Float32Type

32-bit floating-point type

Float64Type

64-bit floating-point type

Float80Type

80-bit floating-point type

Float128Type

128-bit floating-point type

FloatTF32Type

TF32 floating-point type

FunctionType

Map from a list of inputs to a list of results

Syntax:

// Function types may have multiple results.
function-result-type ::= type-list-parens | non-function-type
function-type ::= type-list-parens `->` function-result-type

The function type can be thought of as a function signature. It consists of a list of formal parameter types and a list of formal result types.

Example:

func.func @add_one(%arg0 : i64) -> i64 {
  %c1 = arith.constant 1 : i64
  %0 = arith.addi %arg0, %c1 : i64
  return %0 : i64
}

Parameters:

ParameterC++ typeDescription
inputsArrayRef<Type>
resultsArrayRef<Type>

GraphType

Map from a list of inputs to a list of results

Syntax:

// Function types may have multiple results.
function-result-type ::= type-list-parens | non-function-type
function-type ::= type-list-parens `->` function-result-type

The function type can be thought of as a function signature. It consists of a list of formal parameter types and a list of formal result types.

Example:

func.func @add_one(%arg0 : i64) -> i64 {
  %c1 = arith.constant 1 : i64
  %0 = arith.addi %arg0, %c1 : i64
  return %0 : i64
}

Parameters:

ParameterC++ typeDescription
inputsArrayRef<Type>
resultsArrayRef<Type>

IndexType

Integer-like type with unknown platform-dependent bit width

Syntax:

// Target word-sized integer.
index-type ::= `index`

The index type is a signless integer whose size is equal to the natural machine word of the target ( rationale ) and is used by the affine constructs in MLIR.

Rationale: integers of platform-specific bit widths are practical to express sizes, dimensionalities and subscripts.

IntegerType

Integer type with arbitrary precision up to a fixed limit

Syntax:

// Sized integers like i1, i4, i8, i16, i32.
signed-integer-type ::= `si` [1-9][0-9]*
unsigned-integer-type ::= `ui` [1-9][0-9]*
signless-integer-type ::= `i` [1-9][0-9]*
integer-type ::= signed-integer-type |
                 unsigned-integer-type |
                 signless-integer-type

Integer types have a designated bit width and may optionally have signedness semantics.

Rationale: low precision integers (like i2, i4 etc) are useful for low-precision inference chips, and arbitrary precision integers are useful for hardware synthesis (where a 13 bit multiplier is a lot cheaper/smaller than a 16 bit one).

Parameters:

ParameterC++ typeDescription
widthunsigned
signednessSignednessSemantics

MemRefType

Shaped reference to a region of memory

Syntax:

layout-specification ::= attribute-value
memory-space ::= attribute-value
memref-type ::= `memref` `<` dimension-list-ranked type
                (`,` layout-specification)? (`,` memory-space)? `>`

A memref type is a reference to a region of memory (similar to a buffer pointer, but more powerful). The buffer pointed to by a memref can be allocated, aliased and deallocated. A memref can be used to read and write data from/to the memory region which it references. Memref types use the same shape specifier as tensor types. Note that memref<f32>, memref<0 x f32>, memref<1 x 0 x f32>, and memref<0 x 1 x f32> are all different types.

A memref is allowed to have an unknown rank (e.g. memref<*xf32>). The purpose of unranked memrefs is to allow external library functions to receive memref arguments of any rank without versioning the functions based on the rank. Other uses of this type are disallowed or will have undefined behavior.

Are accepted as elements:

  • built-in integer types;
  • built-in index type;
  • built-in floating point types;
  • built-in vector types with elements of the above types;
  • another memref type;
  • any other type implementing MemRefElementTypeInterface.
Layout

A memref may optionally have a layout that indicates how indices are transformed from the multi-dimensional form into a linear address. The layout must avoid internal aliasing, i.e., two distinct tuples of in-bounds indices must be pointing to different elements in memory. The layout is an attribute that implements MemRefLayoutAttrInterface. The bulitin dialect offers two kinds of layouts: strided and affine map, each of which is available as an attribute. Other attributes may be used to represent the layout as long as they can be converted to a semi-affine map and implement the required interface. Users of memref are expected to fallback to the affine representation when handling unknown memref layouts. Multi-dimensional affine forms are interpreted in row-major fashion.

In absence of an explicit layout, a memref is considered to have a multi-dimensional identity affine map layout. Identity layout maps do not contribute to the MemRef type identification and are discarded on construction. That is, a type with an explicit identity map is memref<?x?xf32, (i,j)->(i,j)> is strictly the same as the one without a layout, memref<?x?xf32>.

Affine Map Layout

The layout may be represented directly as an affine map from the index space to the storage space. For example, the following figure shows an index map which maps a 2-dimensional index from a 2x2 index space to a 3x3 index space, using symbols S0 and S1 as offsets.

Index Map Example

Semi-affine maps are sufficiently flexible to represent a wide variety of dense storage layouts, including row- and column-major and tiled:

// MxN matrix stored in row major layout in memory:
#layout_map_row_major = (i, j) -> (i, j)

// MxN matrix stored in column major layout in memory:
#layout_map_col_major = (i, j) -> (j, i)

// MxN matrix stored in a 2-d blocked/tiled layout with 64x64 tiles.
#layout_tiled = (i, j) -> (i floordiv 64, j floordiv 64, i mod 64, j mod 64)
Strided Layout

Memref layout can be expressed using strides to encode the distance, in number of elements, in (linear) memory between successive entries along a particular dimension. For example, a row-major strided layout for memref<2x3x4xf32> is strided<[12, 4, 1]>, where the last dimension is contiguous as indicated by the unit stride and the remaining strides are products of the sizes of faster-variying dimensions. Strided layout can also express non-contiguity, e.g., memref<2x3, strided<[6, 2]>> only accesses even elements of the dense consecutive storage along the innermost dimension.

The strided layout supports an optional offset that indicates the distance, in the number of elements, between the beginning of the memref and the first accessed element. When omitted, the offset is considered to be zero. That is, memref<2, strided<[2], offset: 0>> and memref<2, strided<[2]>> are strictly the same type.

Both offsets and strides may be dynamic, that is, unknown at compile time. This is represented by using a question mark (?) instead of the value in the textual form of the IR.

The strided layout converts into the following canonical one-dimensional affine form through explicit linearization:

affine_map<(d0, ... dN)[offset, stride0, ... strideN] ->
            (offset + d0 * stride0 + ... dN * strideN)>

Therefore, it is never subject to the implicit row-major layout interpretation.

Codegen of Unranked Memref

Using unranked memref in codegen besides the case mentioned above is highly discouraged. Codegen is concerned with generating loop nests and specialized instructions for high-performance, unranked memref is concerned with hiding the rank and thus, the number of enclosing loops required to iterate over the data. However, if there is a need to code-gen unranked memref, one possible path is to cast into a static ranked type based on the dynamic rank. Another possible path is to emit a single while loop conditioned on a linear index and perform delinearization of the linear index to a dynamic array containing the (unranked) indices. While this is possible, it is expected to not be a good idea to perform this during codegen as the cost of the translations is expected to be prohibitive and optimizations at this level are not expected to be worthwhile. If expressiveness is the main concern, irrespective of performance, passing unranked memrefs to an external C++ library and implementing rank-agnostic logic there is expected to be significantly simpler.

Unranked memrefs may provide expressiveness gains in the future and help bridge the gap with unranked tensors. Unranked memrefs will not be expected to be exposed to codegen but one may query the rank of an unranked memref (a special op will be needed for this purpose) and perform a switch and cast to a ranked memref as a prerequisite to codegen.

Example:

// With static ranks, we need a function for each possible argument type
%A = alloc() : memref<16x32xf32>
%B = alloc() : memref<16x32x64xf32>
call @helper_2D(%A) : (memref<16x32xf32>)->()
call @helper_3D(%B) : (memref<16x32x64xf32>)->()

// With unknown rank, the functions can be unified under one unranked type
%A = alloc() : memref<16x32xf32>
%B = alloc() : memref<16x32x64xf32>
// Remove rank info
%A_u = memref_cast %A : memref<16x32xf32> -> memref<*xf32>
%B_u = memref_cast %B : memref<16x32x64xf32> -> memref<*xf32>
// call same function with dynamic ranks
call @helper(%A_u) : (memref<*xf32>)->()
call @helper(%B_u) : (memref<*xf32>)->()

The core syntax and representation of a layout specification is a semi-affine map. Additionally, syntactic sugar is supported to make certain layout specifications more intuitive to read. For the moment, a memref supports parsing a strided form which is converted to a semi-affine map automatically.

The memory space of a memref is specified by a target-specific attribute. It might be an integer value, string, dictionary or custom dialect attribute. The empty memory space (attribute is None) is target specific.

The notionally dynamic value of a memref value includes the address of the buffer allocated, as well as the symbols referred to by the shape, layout map, and index maps.

Examples of memref static type

// Identity index/layout map
#identity = affine_map<(d0, d1) -> (d0, d1)>

// Column major layout.
#col_major = affine_map<(d0, d1, d2) -> (d2, d1, d0)>

// A 2-d tiled layout with tiles of size 128 x 256.
#tiled_2d_128x256 = affine_map<(d0, d1) -> (d0 div 128, d1 div 256, d0 mod 128, d1 mod 256)>

// A tiled data layout with non-constant tile sizes.
#tiled_dynamic = affine_map<(d0, d1)[s0, s1] -> (d0 floordiv s0, d1 floordiv s1,
                             d0 mod s0, d1 mod s1)>

// A layout that yields a padding on two at either end of the minor dimension.
#padded = affine_map<(d0, d1) -> (d0, (d1 + 2) floordiv 2, (d1 + 2) mod 2)>


// The dimension list "16x32" defines the following 2D index space:
//
//   { (i, j) : 0 <= i < 16, 0 <= j < 32 }
//
memref<16x32xf32, #identity>

// The dimension list "16x4x?" defines the following 3D index space:
//
//   { (i, j, k) : 0 <= i < 16, 0 <= j < 4, 0 <= k < N }
//
// where N is a symbol which represents the runtime value of the size of
// the third dimension.
//
// %N here binds to the size of the third dimension.
%A = alloc(%N) : memref<16x4x?xf32, #col_major>

// A 2-d dynamic shaped memref that also has a dynamically sized tiled
// layout. The memref index space is of size %M x %N, while %B1 and %B2
// bind to the symbols s0, s1 respectively of the layout map #tiled_dynamic.
// Data tiles of size %B1 x %B2 in the logical space will be stored
// contiguously in memory. The allocation size will be
// (%M ceildiv %B1) * %B1 * (%N ceildiv %B2) * %B2 f32 elements.
%T = alloc(%M, %N) [%B1, %B2] : memref<?x?xf32, #tiled_dynamic>

// A memref that has a two-element padding at either end. The allocation
// size will fit 16 * 64 float elements of data.
%P = alloc() : memref<16x64xf32, #padded>

// Affine map with symbol 's0' used as offset for the first dimension.
#imapS = affine_map<(d0, d1) [s0] -> (d0 + s0, d1)>
// Allocate memref and bind the following symbols:
// '%n' is bound to the dynamic second dimension of the memref type.
// '%o' is bound to the symbol 's0' in the affine map of the memref type.
%n = ...
%o = ...
%A = alloc (%n)[%o] : <16x?xf32, #imapS>

Parameters:

ParameterC++ typeDescription
shape::llvm::ArrayRef<int64_t>
elementTypeType
layoutMemRefLayoutAttrInterface
memorySpaceAttribute

NoneType

A unit type

Syntax:

none-type ::= `none`

NoneType is a unit type, i.e. a type with exactly one possible value, where its value does not have a defined dynamic representation.

Example:

func.func @none_type() {
  %none_val = "foo.unknown_op"() : () -> none
  return
}

OpaqueType

Type of a non-registered dialect

Syntax:

opaque-type ::= `opaque` `<` type `>`

Opaque types represent types of non-registered dialects. These are types represented in their raw string form, and can only usefully be tested for type equality.

Example:

opaque<"llvm", "struct<(i32, float)>">
opaque<"pdl", "value">

Parameters:

ParameterC++ typeDescription
dialectNamespaceStringAttr
typeData::llvm::StringRef

RankedTensorType

Multi-dimensional array with a fixed number of dimensions

Syntax:

tensor-type ::= `tensor` `<` dimension-list type (`,` encoding)? `>`
dimension-list ::= (dimension `x`)*
dimension ::= `?` | decimal-literal
encoding ::= attribute-value

Values with tensor type represents aggregate N-dimensional data values, and have a known element type and a fixed rank with a list of dimensions. Each dimension may be a static non-negative decimal constant or be dynamically determined (indicated by ?).

The runtime representation of the MLIR tensor type is intentionally abstracted - you cannot control layout or get a pointer to the data. For low level buffer access, MLIR has a memref type. This abstracted runtime representation holds both the tensor data values as well as information about the (potentially dynamic) shape of the tensor. The dim operation returns the size of a dimension from a value of tensor type.

The encoding attribute provides additional information on the tensor. An empty attribute denotes a straightforward tensor without any specific structure. But particular properties, like sparsity or other specific characteristics of the data of the tensor can be encoded through this attribute. The semantics are defined by a type and attribute interface and must be respected by all passes that operate on tensor types. TODO: provide this interface, and document it further.

Note: hexadecimal integer literals are not allowed in tensor type declarations to avoid confusion between 0xf32 and 0 x f32. Zero sizes are allowed in tensors and treated as other sizes, e.g., tensor<0 x 1 x i32> and tensor<1 x 0 x i32> are different types. Since zero sizes are not allowed in some other types, such tensors should be optimized away before lowering tensors to vectors.

Example:

// Known rank but unknown dimensions.
tensor<? x ? x ? x ? x f32>

// Partially known dimensions.
tensor<? x ? x 13 x ? x f32>

// Full static shape.
tensor<17 x 4 x 13 x 4 x f32>

// Tensor with rank zero. Represents a scalar.
tensor<f32>

// Zero-element dimensions are allowed.
tensor<0 x 42 x f32>

// Zero-element tensor of f32 type (hexadecimal literals not allowed here).
tensor<0xf32>

// Tensor with an encoding attribute (where #ENCODING is a named alias).
tensor<?x?xf64, #ENCODING>

Parameters:

ParameterC++ typeDescription
shape::llvm::ArrayRef<int64_t>
elementTypeType
encodingAttribute

TupleType

Fixed-sized collection of other types

Syntax:

tuple-type ::= `tuple` `<` (type ( `,` type)*)? `>`

The value of tuple type represents a fixed-size collection of elements, where each element may be of a different type.

Rationale: Though this type is first class in the type system, MLIR provides no standard operations for operating on tuple types (rationale).

Example:

// Empty tuple.
tuple<>

// Single element
tuple<f32>

// Many elements.
tuple<i32, f32, tensor<i1>, i5>

Parameters:

ParameterC++ typeDescription
typesArrayRef<Type>

UnrankedMemRefType

Shaped reference, with unknown rank, to a region of memory

Syntax:

unranked-memref-type ::= `memref` `<*x` type (`,` memory-space)? `>`
memory-space ::= attribute-value

A memref type with an unknown rank (e.g. memref<*xf32>). The purpose of unranked memrefs is to allow external library functions to receive memref arguments of any rank without versioning the functions based on the rank. Other uses of this type are disallowed or will have undefined behavior.

See MemRefType for more information on memref types.

Examples:

memref<*f32>

// An unranked memref with a memory space of 10.
memref<*f32, 10>

Parameters:

ParameterC++ typeDescription
elementTypeType
memorySpaceAttribute

UnrankedTensorType

Multi-dimensional array with unknown dimensions

Syntax:

tensor-type ::= `tensor` `<` `*` `x` type `>`

An unranked tensor is a type of tensor in which the set of dimensions have unknown rank. See RankedTensorType for more information on tensor types.

Examples:

tensor<*xf32>

Parameters:

ParameterC++ typeDescription
elementTypeType

VectorType

Multi-dimensional SIMD vector type

Syntax:

vector-type ::= `vector` `<` vector-dim-list vector-element-type `>`
vector-element-type ::= float-type | integer-type | index-type
vector-dim-list := (static-dim-list `x`)?
static-dim-list ::= static-dim (`x` static-dim)*
static-dim ::= (decimal-literal | `[` decimal-literal `]`)

The vector type represents a SIMD style vector used by target-specific operation sets like AVX or SVE. While the most common use is for 1D vectors (e.g. vector<16 x f32>) we also support multidimensional registers on targets that support them (like TPUs). The dimensions of a vector type can be fixed-length, scalable, or a combination of the two. The scalable dimensions in a vector are indicated between square brackets ([ ]).

Vector shapes must be positive decimal integers. 0D vectors are allowed by omitting the dimension: vector<f32>.

Note: hexadecimal integer literals are not allowed in vector type declarations, vector<0x42xi32> is invalid because it is interpreted as a 2D vector with shape (0, 42) and zero shapes are not allowed.

Examples:

// A 2D fixed-length vector of 3x42 i32 elements.
vector<3x42xi32>

// A 1D scalable-length vector that contains a multiple of 4 f32 elements.
vector<[4]xf32>

// A 2D scalable-length vector that contains a multiple of 2x8 f32 elements.
vector<[2]x[8]xf32>

// A 2D mixed fixed/scalable vector that contains 4 scalable vectors of 4 f32 elements.
vector<4x[4]xf32>

// A 3D mixed fixed/scalable vector in which only the inner dimension is
// scalable.
vector<2x[4]x8xf32>

Parameters:

ParameterC++ typeDescription
shape::llvm::ArrayRef<int64_t>
elementType::mlir::TypeVectorElementTypeInterface instance
scalableDims::llvm::ArrayRef<bool>

Comb ops

comb.add (heir::comb::AddOp)

Syntax:

operation ::= `comb.add` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.and (heir::comb::AndOp)

Syntax:

operation ::= `comb.and` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.concat (heir::comb::ConcatOp)

Concatenate a variadic list of operands together.

Syntax:

operation ::= `comb.concat` $inputs attr-dict `:` qualified(type($inputs))

See the comb rationale document for details on operand ordering.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.extract (heir::comb::ExtractOp)

Extract a range of bits into a smaller value, lowBit specifies the lowest bit included.

Syntax:

operation ::= `comb.extract` $input `from` $lowBit attr-dict `:` functional-type($input, $result)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
lowBit::mlir::IntegerAttr32-bit signless integer attribute

Operands:

OperandDescription
inputsignless integer

Results:

ResultDescription
resultsignless integer

comb.icmp (heir::comb::ICmpOp)

Compare two integer values

Syntax:

operation ::= `comb.icmp` (`bin` $twoState^)? $predicate $lhs `,` $rhs attr-dict `:` qualified(type($lhs))

This operation compares two integers using a predicate. If the predicate is true, returns 1, otherwise returns 0. This operation always returns a one bit wide result.

    %r = comb.icmp eq %a, %b : i4

Traits: AlwaysSpeculatableImplTrait, SameTypeOperands

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
predicate::mlir::heir::comb::ICmpPredicateAttrhw.icmp comparison predicate
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
lhssignless integer
rhssignless integer

Results:

ResultDescription
result1-bit signless integer

comb.inv (heir::comb::InvOp)

Syntax:

operation ::= `comb.inv` (`bin` $twoState^)? $input attr-dict `:` qualified(type($input))

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsignless integer

Results:

ResultDescription
resultsignless integer

comb.lut (heir::comb::LUTOp)

Return an integer based on a lookup table

Syntax:

operation ::= `comb.lut` operands attr-dict `:` functional-type(operands, results)

This operation is similar to truth_table, but it allows for an integer output instead of a boolean. Requers an vector of integers as the lookup table, where each integer represents the output for a specific combination of inputs.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
coefficients::mlir::DenseI8ArrayAttri8 dense array attribute
lookupTable::mlir::DenseI8ArrayAttri8 dense array attribute

Operands:

OperandDescription
inputsvariadic of 8-bit signless integer

Results:

ResultDescription
result8-bit signless integer

comb.mul (heir::comb::MulOp)

Syntax:

operation ::= `comb.mul` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.mux (heir::comb::MuxOp)

Return one or the other operand depending on a selector bit

Syntax:

operation ::= `comb.mux` (`bin` $twoState^)? $cond `,` $trueValue `,` $falseValue  attr-dict `:` qualified(type($result))

  %0 = mux %pred, %tvalue, %fvalue : i4

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
cond1-bit signless integer
trueValueany type
falseValueany type

Results:

ResultDescription
resultany type

comb.nand (heir::comb::NandOp)

Syntax:

operation ::= `comb.nand` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.nor (heir::comb::NorOp)

Syntax:

operation ::= `comb.nor` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.or (heir::comb::OrOp)

Syntax:

operation ::= `comb.or` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.parity (heir::comb::ParityOp)

Syntax:

operation ::= `comb.parity` (`bin` $twoState^)? $input attr-dict `:` qualified(type($input))

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsignless integer

Results:

ResultDescription
result1-bit signless integer

comb.replicate (heir::comb::ReplicateOp)

Concatenate the operand a constant number of times

Syntax:

operation ::= `comb.replicate` $input attr-dict `:` functional-type($input, $result)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputsignless integer

Results:

ResultDescription
resultsignless integer

comb.truth_table (heir::comb::TruthTableOp)

Return a true/false based on a lookup table

Syntax:

operation ::= `comb.truth_table` $inputs `->` $lookupTable attr-dict

  %a = ... : i1
  %b = ... : i1
  %0 = comb.truth_table %a, %b -> 6 : ui4

This operation assumes that the lookup table is described as an integer of 2^n bits to fully specify the table. Inputs are sorted MSB -> LSB from left to right and the offset into lookupTable is computed from them. The integer containing the truth table value’s LSB is the output for the input “all false”, and the MSB is the output for the input “all true”.

No difference from array_get into an array of constants except for xprop behavior. If one of the inputs is unknown, but said input doesn’t make a difference in the output (based on the lookup table) the result should not be ‘x’ – it should be the well-known result.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, LUTOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
lookupTable::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
inputsvariadic of 1-bit signless integer

Results:

ResultDescription
result1-bit signless integer

comb.xnor (heir::comb::XNorOp)

Syntax:

operation ::= `comb.xnor` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

comb.xor (heir::comb::XorOp)

Syntax:

operation ::= `comb.xor` (`bin` $twoState^)? $inputs attr-dict `:` qualified(type($result))

Traits: AlwaysSpeculatableImplTrait, Commutative, SameOperandsAndResultType, SameTypeOperands

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
twoState::mlir::UnitAttrunit attribute

Operands:

OperandDescription
inputsvariadic of signless integer

Results:

ResultDescription
resultsignless integer

Comb additional definitions

ICmpPredicate

Hw.icmp comparison predicate

Cases:

SymbolValueString
eq0eq
ne1ne
slt2slt
sle3sle
sgt4sgt
sge5sge
ult6ult
ule7ule
ugt8ugt
uge9uge
ceq10ceq
cne11cne
weq12weq
wne13wne

7.5 - Jaxite

‘jaxite’ Dialect

The jaxite dialect is an exit dialect for generating py code against the jaxite library API, using the jaxite parameters and encoding scheme.

See https://github.com/google/jaxite

Jaxite types

ParamsType

The jaxite security params required to perform homomorphic operations.

Syntax: !jaxite.params

PmapLut3TupleType

A tuple of pmap_lut3 args.

Syntax: !jaxite.pmap_lut3_tuple

ServerKeySetType

The jaxite server key set required to perform homomorphic operations.

Syntax: !jaxite.server_key_set

Jaxite ops

jaxite.constant (heir::jaxite::ConstantOp)

Syntax:

operation ::= `jaxite.constant` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
value1-bit signless integer
paramsThe jaxite security params required to perform homomorphic operations.

Results:

ResultDescription
outputA ciphertext type

jaxite.lut3_args (heir::jaxite::Lut3ArgsOp)

Syntax:

operation ::= `jaxite.lut3_args` operands attr-dict `:` functional-type(operands, results)

The operation computed by this function is generating tuples for pmap_lut3.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
aA ciphertext type
bA ciphertext type
cA ciphertext type
truth_table8-bit signless integer

Results:

ResultDescription
outputA tuple of pmap_lut3 args.

jaxite.lut3 (heir::jaxite::Lut3Op)

Syntax:

operation ::= `jaxite.lut3` operands attr-dict `:` functional-type(operands, results)

The operation computed by this function can be interpreted as

truth_table » {c, b, a}

where {c, b, a} is the unsigned 3-bit integer with bits c, b, a from most significant bit to least-significant bit.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
aA ciphertext type
bA ciphertext type
cA ciphertext type
truth_table8-bit signless integer
serverKeySetThe jaxite server key set required to perform homomorphic operations.
paramsThe jaxite security params required to perform homomorphic operations.

Results:

ResultDescription
outputA ciphertext type

jaxite.pmap_lut3 (heir::jaxite::PmapLut3Op)

Syntax:

operation ::= `jaxite.pmap_lut3` operands attr-dict `:` functional-type(operands, results)

The operation computed by this function is a bacthed Lut3Op.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lut3_argspmap_lut3_tuples
serverKeySetThe jaxite server key set required to perform homomorphic operations.
paramsThe jaxite security params required to perform homomorphic operations.

Results:

ResultDescription
outputlwe-ciphertext-like

7.6 - JaxiteWord

‘jaxiteword’ Dialect

The jaxiteword dialect is an exit dialect for generating py code against the jaxiteword library API, using the jaxiteword parameters and encoding scheme.

See https://github.com/google/jaxite/jaxite_word

JaxiteWord types

CCParamsType

The CCParams required to create CryptoContext.

Syntax: !jaxiteword.cc_params

CiphertextType

Syntax:

!jaxiteword.ciphertext<
  int,   # polys
  int,   # towers
  int   # degrees
>

A ciphertext - a three dimensional array.

Parameters:

ParameterC++ typeDescription
polysint
towersint
degreesint

CryptoContextType

The CryptoContext required to perform homomorphic operations in JaxiteWord.

Syntax: !jaxiteword.crypto_context

EvalKeyType

The evaluation key required to keyswitch/relinearize/rotate/automorphism operation in JaxiteWord.

Syntax: !jaxiteword.eval_key

ModulusListType

Syntax:

!jaxiteword.modulus_list<
  ::llvm::ArrayRef<::mlir::IntegerAttr>   # modulus_list
>

A list of modulus values.

Parameters:

ParameterC++ typeDescription
modulus_list::llvm::ArrayRef<::mlir::IntegerAttr>

PrivateKeyType

The private key required to decrypt a ciphertext in JaxiteWord.

Syntax: !jaxiteword.private_key

PublicKeyType

The public key required to encrypt plaintext in JaxiteWord.

Syntax: !jaxiteword.public_key

JaxiteWord ops

jaxiteword.add (heir::jaxiteword::AddOp)

Syntax:

operation ::= `jaxiteword.add` operands attr-dict `:` functional-type(operands, results)

The operation computed by this function is homomorphic addition.

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
value_a
value_b
modulus_list

Results:

ResultDescription
result

jaxiteword.make_ciphertext (heir::jaxiteword::MakeCiphertextOp)

Create a JaxiteWord ciphertext.

Syntax:

operation ::= `jaxiteword.make_ciphertext` $polys `,` $towers `,` $degrees attr-dict `:` type($ciphertext)

Creates a JaxiteWord ciphertext with the given dimensions.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
polys32-bit signless integer
towers32-bit signless integer
degrees32-bit signless integer

Results:

ResultDescription
ciphertext

7.7 - Lattigo

’lattigo’ Dialect

The lattigo dialect is an exit dialect for generating GO code against the Lattigo library API.

See https://github.com/tuneinsight/lattigo

Lattigo attributes

BGVParametersLiteralAttr

Literal parameters for Lattigo BGV

Syntax:

#lattigo.bgv.parameters_literal<
  int,   # logN
  DenseI64ArrayAttr,   # Q
  DenseI64ArrayAttr,   # P
  DenseI32ArrayAttr,   # logQ
  DenseI32ArrayAttr,   # logP
  int64_t   # plaintextModulus
>

This attribute represents the literal parameters for Lattigo BGV.

This is in accordance with https://pkg.go.dev/github.com/tuneinsight/lattigo/v6@v6.1.0/schemes/bgv#ParametersLiteral where some field are not present in the current implementation.

Users must set the polynomial degree (LogN) and the coefficient modulus, by either setting the Q and P fields to the desired moduli chain, or by setting the LogQ and LogP fields to the desired moduli sizes.

Note that for Lattigo, Q/P requires []uint64, where this attribute only provides int64. We assume user should not select moduli so large to consider the signedness issue.

Users must also specify the coefficient modulus in plaintext-space (T). This modulus must be an NTT-friendly prime in the plaintext space: it must be equal to 1 modulo 2n where n is the plaintext ring degree (i.e., the plaintext space has n slots).

Parameters:

ParameterC++ typeDescription
logNint
QDenseI64ArrayAttr
PDenseI64ArrayAttr
logQDenseI32ArrayAttr
logPDenseI32ArrayAttr
plaintextModulusint64_t

CKKSParametersLiteralAttr

Literal parameters for Lattigo CKKS

Syntax:

#lattigo.ckks.parameters_literal<
  int,   # logN
  DenseI64ArrayAttr,   # Q
  DenseI64ArrayAttr,   # P
  DenseI32ArrayAttr,   # logQ
  DenseI32ArrayAttr,   # logP
  int   # logDefaultScale
>

This attribute represents the literal parameters for Lattigo CKKS.

This is in accordance with https://pkg.go.dev/github.com/tuneinsight/lattigo/v6@v6.1.0/schemes/ckks#ParametersLiteral where some field are not present in the current implementation.

Users must set the polynomial degree (LogN) and the coefficient modulus, by either setting the Q and P fields to the desired moduli chain, or by setting the LogQ and LogP fields to the desired moduli sizes.

Note that for Lattigo, Q/P requires []uint64, where this attribute only provides int64. We assume user should not select moduli so large to consider the signedness issue.

Users must also specify a default initial scale for the plaintexts1.

Parameters:

ParameterC++ typeDescription
logNint
QDenseI64ArrayAttr
PDenseI64ArrayAttr
logQDenseI32ArrayAttr
logPDenseI32ArrayAttr
logDefaultScaleint

Lattigo types

BGVEncoderType

Syntax: !lattigo.bgv.encoder

This type represents the encoder for the BGV encryption scheme.

BGVEvaluatorType

Syntax: !lattigo.bgv.evaluator

This type represents the evaluator for the BGV encryption scheme.

BGVParameterType

Syntax: !lattigo.bgv.parameter

This type represents the parameters for the BGV encryption scheme.

CKKSEncoderType

Syntax: !lattigo.ckks.encoder

This type represents the encoder for the CKKS encryption scheme.

CKKSEvaluatorType

Syntax: !lattigo.ckks.evaluator

This type represents the evaluator for the CKKS encryption scheme.

CKKSParameterType

Syntax: !lattigo.ckks.parameter

This type represents the parameters for the CKKS encryption scheme.

RLWECiphertextType

Syntax: !lattigo.rlwe.ciphertext

This type represents the ciphertext for the RLWE encryption scheme.

RLWEDecryptorType

Syntax: !lattigo.rlwe.decryptor

This type represents the decryptor for the RLWE encryption scheme.

RLWEEncryptorType

Syntax:

!lattigo.rlwe.encryptor<
  bool   # publicKey
>

This type represents the encryptor for the RLWE encryption scheme.

Parameters:

ParameterC++ typeDescription
publicKeybool

RLWEEvaluationKeySetType

Syntax: !lattigo.rlwe.evaluation_key_set

This type represents the evaluation key set for the RLWE encryption scheme.

RLWEGaloisKeyType

Syntax:

!lattigo.rlwe.galois_key<
  ::mlir::IntegerAttr   # galoisElement
>

This type represents the Galois key for the RLWE encryption scheme.

galoisElement: Enabling the automorphism X -> X^{galoisElement}.

Parameters:

ParameterC++ typeDescription
galoisElement::mlir::IntegerAttrAn Attribute containing a integer value

RLWEKeyGeneratorType

Syntax: !lattigo.rlwe.key_generator

This type represents the key generator for the RLWE encryption scheme.

RLWEPlaintextType

Syntax: !lattigo.rlwe.plaintext

This type represents the plaintext for the RLWE encryption scheme.

RLWEPublicKeyType

Syntax: !lattigo.rlwe.public_key

This type represents the public key for the RLWE encryption scheme.

RLWERelinearizationKeyType

Syntax: !lattigo.rlwe.relinearization_key

This type represents the relinearization key for the RLWE encryption scheme.

RLWESecretKeyType

Syntax: !lattigo.rlwe.secret_key

This type represents the secret key for the RLWE encryption scheme.

Lattigo ops

lattigo.bgv.add_new (heir::lattigo::BGVAddNewOp)

Add two ciphertexts in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.add_new` operands attr-dict `:` functional-type(operands, results)

This operation adds two ciphertext values in the Lattigo BGV dialect.

Operands:

OperandDescription
evaluator
lhs
rhsor

Results:

ResultDescription
output

lattigo.bgv.add (heir::lattigo::BGVAddOp)

Add two ciphertexts in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.add` operands attr-dict `:` functional-type(operands, results)

This operation adds two ciphertext values in the Lattigo BGV dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
lhs
rhsor
inplace

Results:

ResultDescription
output

lattigo.bgv.decode (heir::lattigo::BGVDecodeOp)

Decode a plaintext value in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.decode` operands attr-dict `:` functional-type(operands, results)

This operation decodes a plaintext value using the specified encoder in the Lattigo BGV dialect.

The input value tensor should have elements of integer type.

Operands:

OperandDescription
encoder
plaintext
valueranked tensor of integer values

Results:

ResultDescription
decodedranked tensor of integer values

lattigo.bgv.encode (heir::lattigo::BGVEncodeOp)

Encode a plaintext value in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.encode` operands attr-dict `:` functional-type(operands, results)

This operation encodes a plaintext value using the specified encoder in the Lattigo BGV dialect.

The input value tensor should have elements of integer type.

The scale attribute indicates the scaling factor for encoding.

Interfaces: InplaceOpInterface

Attributes:

AttributeMLIR TypeDescription
scale::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
encoder
valueranked tensor of integer values
plaintext

Results:

ResultDescription
encoded

lattigo.bgv.mul_new (heir::lattigo::BGVMulNewOp)

Multiply two ciphertexts in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.mul_new` operands attr-dict `:` functional-type(operands, results)

This operation multiplies two ciphertext values in the Lattigo BGV dialect.

Operands:

OperandDescription
evaluator
lhs
rhsor

Results:

ResultDescription
output

lattigo.bgv.mul (heir::lattigo::BGVMulOp)

Multiply two ciphertexts in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.mul` operands attr-dict `:` functional-type(operands, results)

This operation multiplies two ciphertext values in the Lattigo BGV dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
lhs
rhsor
inplace

Results:

ResultDescription
output

lattigo.bgv.new_encoder (heir::lattigo::BGVNewEncoderOp)

Create a new encoder in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.new_encoder` operands attr-dict `:` functional-type(operands, results)

This operation creates a new encoder for encoding plaintext values in the Lattigo BGV dialect.

Operands:

OperandDescription
params

Results:

ResultDescription
encoder

lattigo.bgv.new_evaluator (heir::lattigo::BGVNewEvaluatorOp)

Create a new evaluator in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.new_evaluator` operands attr-dict `:` functional-type(operands, results)

This operation creates a new evaluator for performing operations on ciphertexts in the Lattigo BGV dialect.

By default, the evaluator is created with the provided parameters and could execute operations which does not relying on evaluation keys.

To support operations that require evaluation keys, the optional evaluation key set should be provided.

The scaleInvariant flag is used to indicate whether the evaluator is for B/FV or BGV. If it is set to true, the evaluator will evaluate operations in B/FV style.

Attributes:

AttributeMLIR TypeDescription
scaleInvariant::mlir::BoolAttrbool attribute

Operands:

OperandDescription
params
evaluationKeySet

Results:

ResultDescription
evaluator

lattigo.bgv.new_parameters_from_literal (heir::lattigo::BGVNewParametersFromLiteralOp)

Create new BGV parameters from a literal in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.new_parameters_from_literal` operands attr-dict `:` functional-type(operands, results)

This operation creates new BGV parameters from a given literal value in the Lattigo BGV dialect.

Attributes:

AttributeMLIR TypeDescription
paramsLiteral::mlir::heir::lattigo::BGVParametersLiteralAttrLiteral parameters for Lattigo BGV

Results:

ResultDescription
params

lattigo.bgv.new_plaintext (heir::lattigo::BGVNewPlaintextOp)

Create a new plaintext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.new_plaintext` operands attr-dict `:` functional-type(operands, results)

This operation creates a new plaintext value in the Lattigo BGV dialect.

Operands:

OperandDescription
params

Results:

ResultDescription
plaintext

lattigo.bgv.relinearize_new (heir::lattigo::BGVRelinearizeNewOp)

Relinearize a ciphertext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.relinearize_new` operands attr-dict `:` functional-type(operands, results)

This operation relinearizes a ciphertext value in the Lattigo BGV dialect.

Operands:

OperandDescription
evaluator
input

Results:

ResultDescription
output

lattigo.bgv.relinearize (heir::lattigo::BGVRelinearizeOp)

Relinearize a ciphertext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.relinearize` operands attr-dict `:` functional-type(operands, results)

This operation relinearizes a ciphertext value in the Lattigo BGV dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
input
inplace

Results:

ResultDescription
output

lattigo.bgv.rescale_new (heir::lattigo::BGVRescaleNewOp)

Rescale a ciphertext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.rescale_new` operands attr-dict `:` functional-type(operands, results)

This operation rescales a ciphertext value in the Lattigo BGV dialect.

Operands:

OperandDescription
evaluator
input

Results:

ResultDescription
output

lattigo.bgv.rescale (heir::lattigo::BGVRescaleOp)

Rescale a ciphertext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.rescale` operands attr-dict `:` functional-type(operands, results)

This operation rescales a ciphertext value in the Lattigo BGV dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
input
inplace

Results:

ResultDescription
output

lattigo.bgv.rotate_columns_new (heir::lattigo::BGVRotateColumnsNewOp)

Rotate columns of a ciphertext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.rotate_columns_new` operands attr-dict `:` functional-type(operands, results)

This operation rotates the columns of a ciphertext value in the Lattigo BGV dialect.

Lattigo exposes the SIMD slot of BGV as a N/2 x 2 matrix, where N/2 is the column.

Offset is valid for both positive and negative number.

Attributes:

AttributeMLIR TypeDescription
offset::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
evaluator
input

Results:

ResultDescription
output

lattigo.bgv.rotate_columns (heir::lattigo::BGVRotateColumnsOp)

Rotate columns of a ciphertext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.rotate_columns` operands attr-dict `:` functional-type(operands, results)

This operation rotates the columns of a ciphertext value in the Lattigo BGV dialect.

Lattigo exposes the SIMD slot of BGV as a N/2 x 2 matrix, where N/2 is the column.

Offset is valid for both positive and negative number.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Attributes:

AttributeMLIR TypeDescription
offset::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
evaluator
input
inplace

Results:

ResultDescription
output

lattigo.bgv.rotate_rows_new (heir::lattigo::BGVRotateRowsNewOp)

Rotate rows of a ciphertext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.rotate_rows_new` operands attr-dict `:` functional-type(operands, results)

This operation swap the rows of a ciphertext value in the Lattigo BGV dialect.

Lattigo exposes the SIMD slot of BGV as a N/2 x 2 matrix, where 2 is the row.

Operands:

OperandDescription
evaluator
input

Results:

ResultDescription
output

lattigo.bgv.rotate_rows (heir::lattigo::BGVRotateRowsOp)

Rotate rows of a ciphertext in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.rotate_rows` operands attr-dict `:` functional-type(operands, results)

This operation swap the rows of a ciphertext value in the Lattigo BGV dialect.

Lattigo exposes the SIMD slot of BGV as a N/2 x 2 matrix, where 2 is the row.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
input
inplace

Results:

ResultDescription
output

lattigo.bgv.sub_new (heir::lattigo::BGVSubNewOp)

Subtract two ciphertexts in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.sub_new` operands attr-dict `:` functional-type(operands, results)

This operation subtracts one ciphertext value from another in the Lattigo BGV dialect.

Operands:

OperandDescription
evaluator
lhs
rhsor

Results:

ResultDescription
output

lattigo.bgv.sub (heir::lattigo::BGVSubOp)

Subtract two ciphertexts in the Lattigo BGV dialect

Syntax:

operation ::= `lattigo.bgv.sub` operands attr-dict `:` functional-type(operands, results)

This operation subtracts one ciphertext value from another in the Lattigo BGV dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
lhs
rhsor
inplace

Results:

ResultDescription
output

lattigo.ckks.add_new (heir::lattigo::CKKSAddNewOp)

Add two ciphertexts in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.add_new` operands attr-dict `:` functional-type(operands, results)

This operation adds two ciphertext values in the Lattigo CKKS dialect.

Operands:

OperandDescription
evaluator
lhs
rhsor

Results:

ResultDescription
output

lattigo.ckks.add (heir::lattigo::CKKSAddOp)

Add two ciphertexts in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.add` operands attr-dict `:` functional-type(operands, results)

This operation adds two ciphertext values in the Lattigo CKKS dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
lhs
rhsor
inplace

Results:

ResultDescription
output

lattigo.ckks.decode (heir::lattigo::CKKSDecodeOp)

Decode a plaintext value in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.decode` operands attr-dict `:` functional-type(operands, results)

This operation decodes a plaintext value using the specified encoder in the Lattigo CKKS dialect.

The input value tensor should have elements of float type or complex type.

Operands:

OperandDescription
encoder
plaintext
valueranked tensor of floating-point or complex-type values

Results:

ResultDescription
decodedranked tensor of floating-point or complex-type values

lattigo.ckks.encode (heir::lattigo::CKKSEncodeOp)

Encode a plaintext value in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.encode` operands attr-dict `:` functional-type(operands, results)

This operation encodes a plaintext value using the specified encoder in the Lattigo CKKS dialect.

The input value tensor should have elements of float type or complex type.

The scale attribute indicates the scaling factor for encoding.

Interfaces: InplaceOpInterface

Attributes:

AttributeMLIR TypeDescription
scale::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
encoder
valueranked tensor of floating-point or complex-type values
plaintext

Results:

ResultDescription
encoded

lattigo.ckks.mul_new (heir::lattigo::CKKSMulNewOp)

Multiply two ciphertexts in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.mul_new` operands attr-dict `:` functional-type(operands, results)

This operation multiplies two ciphertext values in the Lattigo CKKS dialect.

Operands:

OperandDescription
evaluator
lhs
rhsor

Results:

ResultDescription
output

lattigo.ckks.mul (heir::lattigo::CKKSMulOp)

Multiply two ciphertexts in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.mul` operands attr-dict `:` functional-type(operands, results)

This operation multiplies two ciphertext values in the Lattigo CKKS dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
lhs
rhsor
inplace

Results:

ResultDescription
output

lattigo.ckks.new_encoder (heir::lattigo::CKKSNewEncoderOp)

Create a new encoder in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.new_encoder` operands attr-dict `:` functional-type(operands, results)

This operation creates a new encoder for encoding plaintext values in the Lattigo CKKS dialect.

Operands:

OperandDescription
params

Results:

ResultDescription
encoder

lattigo.ckks.new_evaluator (heir::lattigo::CKKSNewEvaluatorOp)

Create a new evaluator in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.new_evaluator` operands attr-dict `:` functional-type(operands, results)

This operation creates a new evaluator for performing operations on ciphertexts in the Lattigo CKKS dialect.

By default, the evaluator is created with the provided parameters and could execute operations which does not relying on evaluation keys.

To support operations that require evaluation keys, the optional evaluation key set should be provided.

Operands:

OperandDescription
params
evaluationKeySet

Results:

ResultDescription
evaluator

lattigo.ckks.new_parameters_from_literal (heir::lattigo::CKKSNewParametersFromLiteralOp)

Create new CKKS parameters from a literal in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.new_parameters_from_literal` operands attr-dict `:` functional-type(operands, results)

This operation creates new CKKS parameters from a given literal value in the Lattigo CKKS dialect.

Attributes:

AttributeMLIR TypeDescription
paramsLiteral::mlir::heir::lattigo::CKKSParametersLiteralAttrLiteral parameters for Lattigo CKKS

Results:

ResultDescription
params

lattigo.ckks.new_plaintext (heir::lattigo::CKKSNewPlaintextOp)

Create a new plaintext in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.new_plaintext` operands attr-dict `:` functional-type(operands, results)

This operation creates a new plaintext value in the Lattigo CKKS dialect.

Operands:

OperandDescription
params

Results:

ResultDescription
plaintext

lattigo.ckks.relinearize_new (heir::lattigo::CKKSRelinearizeNewOp)

Relinearize a ciphertext in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.relinearize_new` operands attr-dict `:` functional-type(operands, results)

This operation relinearizes a ciphertext value in the Lattigo CKKS dialect.

Operands:

OperandDescription
evaluator
input

Results:

ResultDescription
output

lattigo.ckks.relinearize (heir::lattigo::CKKSRelinearizeOp)

Relinearize a ciphertext in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.relinearize` operands attr-dict `:` functional-type(operands, results)

This operation relinearizes a ciphertext value in the Lattigo CKKS dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
input
inplace

Results:

ResultDescription
output

lattigo.ckks.rescale_new (heir::lattigo::CKKSRescaleNewOp)

Rescale a ciphertext in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.rescale_new` operands attr-dict `:` functional-type(operands, results)

This operation rescales a ciphertext value in the Lattigo CKKS dialect.

Operands:

OperandDescription
evaluator
input

Results:

ResultDescription
output

lattigo.ckks.rescale (heir::lattigo::CKKSRescaleOp)

Rescale a ciphertext in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.rescale` operands attr-dict `:` functional-type(operands, results)

This operation rescales a ciphertext value in the Lattigo CKKS dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
input
inplace

Results:

ResultDescription
output

lattigo.ckks.rotate_new (heir::lattigo::CKKSRotateNewOp)

Rotate slots of a ciphertext in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.rotate_new` operands attr-dict `:` functional-type(operands, results)

This operation rotates slots of a ciphertext value in the Lattigo CKKS dialect.

For vanilla CKKS, the maximum number of slots is N/2 with each slot being complex number. Lattigo also support a conjugate-invariant version of CKKS, i.e. the ring is Z[X + X^{-1} ]/(X^N+1), which allows for a maximum of N slots with each slot being real number.

Offset is valid for both positive and negative number.

Attributes:

AttributeMLIR TypeDescription
offset::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
evaluator
input

Results:

ResultDescription
output

lattigo.ckks.rotate (heir::lattigo::CKKSRotateOp)

Rotate slots of a ciphertext in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.rotate` operands attr-dict `:` functional-type(operands, results)

This operation rotates slots of a ciphertext value in the Lattigo CKKS dialect.

For vanilla CKKS, the maximum number of slots is N/2 with each slot being complex number. Lattigo also support a conjugate-invariant version of CKKS, i.e. the ring is Z[X + X^{-1} ]/(X^N+1), which allows for a maximum of N slots with each slot being real number.

Offset is valid for both positive and negative number.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Attributes:

AttributeMLIR TypeDescription
offset::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
evaluator
input
inplace

Results:

ResultDescription
output

lattigo.ckks.sub_new (heir::lattigo::CKKSSubNewOp)

Subtract two ciphertexts in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.sub_new` operands attr-dict `:` functional-type(operands, results)

This operation subtracts one ciphertext value from another in the Lattigo CKKS dialect.

Operands:

OperandDescription
evaluator
lhs
rhsor

Results:

ResultDescription
output

lattigo.ckks.sub (heir::lattigo::CKKSSubOp)

Subtract two ciphertexts in the Lattigo CKKS dialect

Syntax:

operation ::= `lattigo.ckks.sub` operands attr-dict `:` functional-type(operands, results)

This operation subtracts one ciphertext value from another in the Lattigo CKKS dialect.

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluator
lhs
rhsor
inplace

Results:

ResultDescription
output

lattigo.rlwe.decrypt (heir::lattigo::RLWEDecryptOp)

Decrypts a ciphertext using RLWE

Syntax:

operation ::= `lattigo.rlwe.decrypt` operands attr-dict `:` functional-type(operands, results)

This operation decrypts a ciphertext using RLWE

Operands:

OperandDescription
decryptor
ciphertext

Results:

ResultDescription
plaintext

lattigo.rlwe.drop_level_new (heir::lattigo::RLWEDropLevelNewOp)

Drop level of a ciphertext

Syntax:

operation ::= `lattigo.rlwe.drop_level_new` operands attr-dict `:` functional-type(operands, results)

Attributes:

AttributeMLIR TypeDescription
levelToDrop::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
evaluatoror
input

Results:

ResultDescription
output

lattigo.rlwe.drop_level (heir::lattigo::RLWEDropLevelOp)

Drop level of a ciphertext

Syntax:

operation ::= `lattigo.rlwe.drop_level` operands attr-dict `:` functional-type(operands, results)

This operation drops the level of a ciphertext

The result will be written to the inplace operand. The outputresult is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Attributes:

AttributeMLIR TypeDescription
levelToDrop::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
evaluatoror
input
inplace

Results:

ResultDescription
output

lattigo.rlwe.encrypt (heir::lattigo::RLWEEncryptOp)

Encrypts a plaintext using RLWE

Syntax:

operation ::= `lattigo.rlwe.encrypt` operands attr-dict `:` functional-type(operands, results)

This operation encrypts a plaintext using RLWE

Operands:

OperandDescription
encryptor
plaintext

Results:

ResultDescription
ciphertext

lattigo.rlwe.gen_galois_key (heir::lattigo::RLWEGenGaloisKeyOp)

Generates a new RLWE Galois key

Syntax:

operation ::= `lattigo.rlwe.gen_galois_key` operands attr-dict `:` functional-type(operands, results)

This operation generates a new RLWE Galois key

galoisElement: Enabling the automorphism X -> X^{galoisElement}.

Attributes:

AttributeMLIR TypeDescription
galoisElement::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
keyGenerator
secretKey

Results:

ResultDescription
galoisKey

lattigo.rlwe.gen_key_pair (heir::lattigo::RLWEGenKeyPairOp)

Generates a new RLWE key pair

Syntax:

operation ::= `lattigo.rlwe.gen_key_pair` operands attr-dict `:` functional-type(operands, results)

This operation generates a new RLWE key pair

Operands:

OperandDescription
keyGenerator

Results:

ResultDescription
secretKey
publicKey

lattigo.rlwe.gen_relinearization_key (heir::lattigo::RLWEGenRelinearizationKeyOp)

Generates a new RLWE relinearization key

Syntax:

operation ::= `lattigo.rlwe.gen_relinearization_key` operands attr-dict `:` functional-type(operands, results)

This operation generates a new RLWE relinearization key

Operands:

OperandDescription
keyGenerator
secretKey

Results:

ResultDescription
relinearizationKey

lattigo.rlwe.negate_new (heir::lattigo::RLWENegateNewOp)

Negate a ciphertext

Syntax:

operation ::= `lattigo.rlwe.negate_new` operands attr-dict `:` functional-type(operands, results)

Operands:

OperandDescription
evaluatoror
input

Results:

ResultDescription
output

lattigo.rlwe.negate (heir::lattigo::RLWENegateOp)

Negate of a ciphertext

Syntax:

operation ::= `lattigo.rlwe.negate` operands attr-dict `:` functional-type(operands, results)

This operation negates a ciphertext

The result will be written to the inplace operand. The output result is a transitive reference to the inplace operand for sake of the MLIR SSA form.

Interfaces: InplaceOpInterface

Operands:

OperandDescription
evaluatoror
input
inplace

Results:

ResultDescription
output

lattigo.rlwe.new_decryptor (heir::lattigo::RLWENewDecryptorOp)

Creates a new RLWE decryptor

Syntax:

operation ::= `lattigo.rlwe.new_decryptor` operands attr-dict `:` functional-type(operands, results)

This operation creates a new RLWE decryptor

Operands:

OperandDescription
paramsor
secretKey

Results:

ResultDescription
decryptor

lattigo.rlwe.new_encryptor (heir::lattigo::RLWENewEncryptorOp)

Creates a new RLWE encryptor

Syntax:

operation ::= `lattigo.rlwe.new_encryptor` operands attr-dict `:` functional-type(operands, results)

This operation creates a new RLWE encryptor

Operands:

OperandDescription
paramsor
encryptionKeyor

Results:

ResultDescription
encryptor

lattigo.rlwe.new_evaluation_key_set (heir::lattigo::RLWENewEvaluationKeySetOp)

Generates a new RLWE evaluation key set

Syntax:

operation ::= `lattigo.rlwe.new_evaluation_key_set` operands attr-dict `:` functional-type(operands, results)

This operation generates a new RLWE evaluation key set

Operands:

OperandDescription
keysvariadic of any type

Results:

ResultDescription
evaluationKeySet

lattigo.rlwe.new_key_generator (heir::lattigo::RLWENewKeyGeneratorOp)

Generates a new RLWE key generator

Syntax:

operation ::= `lattigo.rlwe.new_key_generator` operands attr-dict `:` functional-type(operands, results)

This operation generates a new RLWE key generator

Operands:

OperandDescription
paramsor

Results:

ResultDescription
keyGenerator

7.8 - LWE

’lwe’ Dialect

The lwe dialect is a dialect for concepts related to cryptosystems in the Learning With Errors (LWE) family.

See Wikipedia for an overview of LWE and the related RLWE problem.

While one might expect this dialect to contain types along the lines of LWE and RLWE ciphertexts, and operations like encryption, decryption, adding and multiplying ciphertexts, these concepts are not centralized here because they are too scheme-specific.

Instead, this dialect provides attributes that can be attached to tensors of integer or poly.poly types, which indicate that they are semantically LWE and RLWE ciphertexts, respectively.

LWE attributes

ApplicationDataAttr

Syntax:

#lwe.application_data<
  mlir::Type,   # message_type
  Attribute   # overflow
>

An attribute describing the semantics of the underlying application data.

The messageType parameter is used to describe the type and bits of the original application data, e.g. i1, i32, f32. This type is later mapped into the plaintext space of an FHE scheme by embedding, scaling, or other techniques.

This attribute also contains information about the overflow semantics of the data in the application. By default, we assume that the application program was written so that the overflow is not expected and the overflow attribute can can be no_overflow. For LWE-based CGGI ciphertexts, the overflow attribute will usually be preserve_overflow, since messages will overflow into padding bits.

Parameters:

ParameterC++ typeDescription
message_typemlir::Type
overflowAttribute

CiphertextSpaceAttr

Syntax:

#lwe.ciphertext_space<
  ::mlir::heir::polynomial::RingAttr,   # ring
  ::mlir::heir::lwe::LweEncryptionType,   # encryption_type
  unsigned   # size
>

An attribute describing the ciphertext space and the transformation from plaintext space to ciphertext space of an FHE scheme.

The ciphertext space information includes the ring attribute, describing the space that the ciphertext elements belong to. The ring attribute contains a coefficient type attribute that describes the semantics of the coefficient. For example, a ring modulo $1 + x^1024$ with coefficients modulo $q = 298374$ will be described as

!cmod = !mod_arith.int<298374 : i64>
#ring = #polynomial.ring<coefficientType = !cmod, polynomialModulus = <1 + x**1024>>
#ciphertext_space = #lwe.ciphertext_space<ring = #ring, encryption_type = lsb>

Ciphertexts using an RNS representation for $q$ will use an RNS type in their ring’s coefficient type attribute.

!limb1 = !mod_arith.int<2251799814045697 : i64>
!limb2 = !mod_arith.int<65537 : i64>
#rns_mod = !rns.rns<!limb1, !limb2>
#ring = #polynomial.ring<coefficientType = #rns_mod, polynomialModulus = <1 + x**1024>>
#ciphertext_space = #lwe.ciphertext_space<ring = #ring, encryption_type = lsb>

Scalar LWE ciphertexts (like those used in CGGI) use an ideal polynomial of degree 1, $x$. CGGI ciphertexts will typically use a power of two modulus and may use a native integer type for its coefficient modulus.

#ring = #polynomial.ring<coefficientType = i32, polynomialModulus = <1 + x**1024>>
#ciphertext_space = #lwe.ciphertext_space<ring = #ring, encryption_type = lsb>

The ciphertext encoding info is used to describe the way the plaintext data is encoded into the ciphertext (in the MSB, LSB, or mixed).

The size parameter is used to describe the number of polynomials comprising the ciphertext. This is typically 2 for RLWE ciphertexts that are made up of an $(a, b)$ pair and greater than 2 for LWE instances. For example, after an RLWE multiplication of two size 2 ciphertexts, the ciphertext’s size will be 3.

Parameters:

ParameterC++ typeDescription
ring::mlir::heir::polynomial::RingAttr
encryption_type::mlir::heir::lwe::LweEncryptionType
sizeunsigned

CoefficientEncodingAttr

An encoding of cleartexts directly as coefficients.

Syntax:

#lwe.coefficient_encoding<
  int64_t   # scaling_factor
>

A coefficient encoding of a list of integers asserts that the coefficients of the polynomials contain the integers, with the same semantics as constant_coefficient_encoding for per-coefficient encodings.

A scaling_factor is optionally applied on the scalar when converting from a rounded floating point to an integer.

Example:

#coeff_encoding = #lwe.coefficient_encoding<scaling_factor=10000>

Parameters:

ParameterC++ typeDescription
scaling_factorint64_t

ConstantCoefficientEncodingAttr

An encoding of a scalar in the constant coefficient

Syntax:

#lwe.constant_coefficient_encoding<
  int64_t   # scaling_factor
>

An encoding of a single scalar into the constant coefficient of the plaintext.

All other coefficients of the plaintext are set to be zero. This encoding is used to encode scalar LWE ciphertexts where the plaintext space is viewed as a polynomial ring modulo x.

The scalar is first multiplied by the scaling_factor and then rounded to the nearest integer before encoding into the plaintext coefficient.

Example:

#coeff_encoding = #lwe.constant_coefficient_encoding<scaling_factor=10000>

Parameters:

ParameterC++ typeDescription
scaling_factorint64_t

FullCRTPackingEncodingAttr

An encoding of cleartexts via CRT slots.

Syntax:

#lwe.full_crt_packing_encoding<
  int64_t   # scaling_factor
>

This encoding maps a list of integers via the Chinese Remainder Theorem (CRT) into the plaintext space.

Given a ring with irreducible ideal polynomial f(x) and coefficient modulus q, f(x) can be decomposed modulo q into a direct product of lower-degree polynomials. This allows full SIMD-style homomorphic operations across the slots formed from each factor.

This attribute can only be used in the context of on full CRT packing, where the polynomial f(x) splits completely (into linear factors) and the number of slots equals the degree of f(x). This happens when q is prime and q = 1 mod n.

A scaling_factor is optionally applied on the scalar when converting from a rounded floating point to an integer.

Example:

#coeff_encoding = #lwe.full_crt_packing_encoding<scaling_factor=10000>

Parameters:

ParameterC++ typeDescription
scaling_factorint64_t

InverseCanonicalEncodingAttr

An encoding of cleartexts via the inverse canonical embedding.

Syntax:

#lwe.inverse_canonical_encoding<
  int64_t   # scaling_factor
>

Let $n$ be the degree of the polynomials in the plaintext space. An “inverse_canonical_encoding” of a list of real or complex values $v_1, \dots, v_{n/2}$ is (almost) the inverse of the following decoding map.

Define a map $\tau_N$ that maps a polynomial $p \in \mathbb{Z}[x] / (x^N + 1) \to \mathbb{C}^{N/2}$ by evaluating it at the following $N/2$ points, where $\omega = e^{2 \pi i / 2N}$ is the primitive $2N$th root of unity:

[ \omega, \omega^3, \omega^5, \dots, \omega^{N-1} ]

Then the complete decoding operation is $\textup{Decode}(p) = (1/\Delta)\tau_N(p)$, where $\Delta$ is a scaling parameter and $\tau_N$ is the truncated canonical embedding above. The encoding operation is the inverse of the decoding operation, with some caveats explained below.

The map $\tau_N$ is derived from the so-called canonical embedding $\tau$, though in the standard canonical embedding, we evaluate at all odd powers of the root of unity, $\omega, \omega^3, \dots, \omega^{2N-1}$. For polynomials in the slightly larger space $\mathbb{R}[x] / (x^N + 1)$, the image of the canonical embedding is the subspace $H \subset \mathbb{C}^N$ defined by tuples $(z_1, \dots, z_N)$ such that $\overline{z_i} = \overline{z_{N-i+1}}$. Note that this property holds because polynomial evaluation commutes with complex conjugates, and the second half of the roots of unity evaluate are complex conjugates of the first half. The converse, that any such tuple with complex conjugate symmetry has an inverse under $\tau$ with all real coefficients, makes $\tau$ is a bijection onto $H$. $\tau$ and its inverse are explicitly computable as discrete Fourier Transforms.

Because of the symmetry in canonical embedding for real polynomials, inputs to this encoding can be represented as a list of $N/2$ complex points, with the extra symmetric structure left implicit. $\tau_N$ and its inverse can also be explicitly computed without need to expand the vectors to length $N$.

The rounding step is required to invert the decoding because, while cleartexts must be (implicitly) in the subspace $H$, they need not be the output of $\tau_N$ for an integer polynomial. The rounding step ensures we can use integer polynomial plaintexts for the FHE operations. There are multiple rounding mechanisms, and this attribute does not specify which is used, because in theory two ciphertexts that have used different roundings are still compatible, though they may have different noise growth patterns.

The scaling parameter $\Delta$ is specified by the scaling_factor, which are applied coefficient-wise using the same semantics as the constant_coefficient_encoding.

A typical flow for the CKKS scheme using this encoding would be to apply an inverse FFT operation to invert the canonical embedding to be a polynomial with real coefficients, then encrypt scale the resulting polynomial’s coefficients according to the scaling parameters, then round to get integer coefficients.

Example:

#canonical_encoding = #lwe.inverse_canonical_encoding<scaling_factor=10000>

Parameters:

ParameterC++ typeDescription
scaling_factorint64_t

KeyAttr

Syntax:

#lwe.key<
  int   # slot_index
>

An attribute describing the key with which the message is currently encrypted.

The key attribute describes the key with which the message is currently encrypted and decryption can be performed. For example, if the decryption of a ciphertext $c = (c_0(x), c_1(x))$ is performed by computing the inner product $(c_0(x), c_1(x)) \cdot (1, s(x))$ then the key is $(1, s(x))$.

The slot_index describes the key after using a Galois automorphism to rotate the plaintext slots by slot_index. This will correspond to an action $\phi_k: x \rightarrow x^k$ for some k that depends on the structure of the Galois group for the chosen scheme parameters. The corresponding key will have a new basis $(1, s(x^(k)))$.

Parameters:

ParameterC++ typeDescription
slot_indexint

ModulusChainAttr

Syntax:

#lwe.modulus_chain<
  ::llvm::ArrayRef<mlir::IntegerAttr>,   # elements
  int   # current
>

An attribute describing the elements of the modulus chain of an RLWE scheme.

Parameters:

ParameterC++ typeDescription
elements::llvm::ArrayRef<mlir::IntegerAttr>
currentint

NoOverflowAttr

An attribute informing that application data never overflows.

Syntax: #lwe.no_overflow

This attribute informs lowerings that a program is written so that the message data will never overflow beyond the message type.

// FIXME: Have a separate WraparoundOverflow, which lowers the same as NoOverflow?

PlaintextSpaceAttr

Syntax:

#lwe.plaintext_space<
  ::mlir::heir::polynomial::RingAttr,   # ring
  Attribute   # encoding
>

An attribute describing the plaintext space and the transformation from application data to plaintext space of an FHE scheme.

The plaintext space information is the ring structure, which contains the plaintext modulus $t$, which may be a power of two in the case of CGGI ciphertexts, or a prime power for RLWE. LWE ciphertexts use the ideal polynomial of degree 1 $x$. The plaintext modulus used in LWE-based CGGI plaintexts describes the full message space $\mathbb{Z}_p$ including the padding bits. The application data info attribute describes the space $\mathbb{Z}_p’$ where $p’ < p$ that the underlying message belongs to.

For RLWE schemes, this will include the type of encoding of application data integers to a plaintext space Z_p[X]/X^N + 1. This may be a constant coefficient encoding, CRT-based packing for SIMD semantics, or other slot packing. When using full CRT packing, the ring must split into linear factors. The CKKS scheme will also include attributes describing the complex encoding, including the scaling factor, which will change after multiplication and rescaling.

Parameters:

ParameterC++ typeDescription
ring::mlir::heir::polynomial::RingAttr
encodingAttributeAn encoding of a scalar in the constant coefficient or An encoding of cleartexts directly as coefficients. or An encoding of cleartexts via the inverse canonical embedding. or An encoding of cleartexts via CRT slots.

PreserveOverflowAttr

An attribute informing that application data overflows in the message type.

Syntax: #lwe.preserve_overflow

This attribute informs lowerings that a program is written so that the message data may overflow beyond the message type.

LWE types

LWECiphertextType

A ciphertext type

Syntax:

!lwe.lwe_ciphertext<
  ApplicationDataAttr,   # application_data
  PlaintextSpaceAttr,   # plaintext_space
  CiphertextSpaceAttr,   # ciphertext_space
  KeyAttr,   # key
  ModulusChainAttr   # modulus_chain
>

An LWE ciphertext will always contain the application data, plaintext space, ciphertext space, and key information.

A modulus chain is optionally specified for parameter choices in RLWE schemes that use more than one of modulus. When no modulus chain is specified, the ciphertext modulus is always the ciphertext ring’s coefficient modulus.

Parameters:

ParameterC++ typeDescription
application_dataApplicationDataAttr
plaintext_spacePlaintextSpaceAttr
ciphertext_spaceCiphertextSpaceAttr
keyKeyAttr
modulus_chainModulusChainAttr

LWEPlaintextType

A plaintext type

Syntax:

!lwe.lwe_plaintext<
  ApplicationDataAttr,   # application_data
  PlaintextSpaceAttr   # plaintext_space
>

Parameters:

ParameterC++ typeDescription
application_dataApplicationDataAttr
plaintext_spacePlaintextSpaceAttr

LWEPublicKeyType

A public key for LWE

Syntax:

!lwe.lwe_public_key<
  KeyAttr,   # key
  ::mlir::heir::polynomial::RingAttr   # ring
>

Parameters:

ParameterC++ typeDescription
keyKeyAttr
ring::mlir::heir::polynomial::RingAttr

LWESecretKeyType

A secret key for LWE

Syntax:

!lwe.lwe_secret_key<
  KeyAttr,   # key
  ::mlir::heir::polynomial::RingAttr   # ring
>

Parameters:

ParameterC++ typeDescription
keyKeyAttr
ring::mlir::heir::polynomial::RingAttr

LWE ops

lwe.add (heir::lwe::AddOp)

Add two LWE ciphertexts

Syntax:

operation ::= `lwe.add` operands attr-dict `:` type($output)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.encode (heir::lwe::EncodeOp)

Encode an integer to yield an LWE plaintext

Syntax:

operation ::= `lwe.encode` $input attr-dict `:` qualified(type($input)) `to` qualified(type($output))

Encode an integer to yield an LWE plaintext.

This op uses an overflow attribute to indicate the overflow semantics. For CGGI ciphertexts, this will typically be preserve_overflow to indicate that the message bits can overflow into the carry bit space.

The LWE plaintext ring is constructed with a plaintext bit width using plaintext_bits and a polynomial modulus of x.

Examples:

%Y = lwe.encode %value {overflow = #overflow, plaintext_bits = 3}: i1 to !lwe.lwe_plaintext<application_data = #app_data, plaintext_space = #space>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
plaintext_bits::mlir::IntegerAttrindex attribute
overflow::mlir::AttributeAn attribute informing that application data never overflows. or An attribute informing that application data overflows in the message type.

Operands:

OperandDescription
inputsignless-integer-like or floating-point-like

Results:

ResultDescription
outputA plaintext type

lwe.mul_scalar (heir::lwe::MulScalarOp)

Multiply an LWE ciphertext by a scalar

Syntax:

operation ::= `lwe.mul_scalar` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
ciphertextlwe-ciphertext-like
scalarinteger

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.radd (heir::lwe::RAddOp)

Add two RLWE ciphertexts

Syntax:

operation ::= `lwe.radd` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultPlaintextTypes, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.radd_plain (heir::lwe::RAddPlainOp)

Addition between RLWE ciphertext-plaintext

Syntax:

operation ::= `lwe.radd_plain` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, InferTypeOpAdaptor, IsCiphertextPlaintextOp, SameOperandsAndResultPlaintextTypes

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.rlwe_decode (heir::lwe::RLWEDecodeOp)

Decode an RLWE plaintext to an underlying type

Syntax:

operation ::= `lwe.rlwe_decode` $input attr-dict `:` qualified(type($input)) `->` qualified(type($output))

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
encoding::mlir::AttributeAn encoding of a scalar in the constant coefficient or An encoding of cleartexts directly as coefficients. or An encoding of cleartexts via the inverse canonical embedding. or An encoding of cleartexts via CRT slots.
ring::mlir::heir::polynomial::RingAttran attribute specifying a polynomial ring

Operands:

OperandDescription
inputA plaintext type

Results:

ResultDescription
outputsignless-integer-like or floating-point-like

lwe.rlwe_decrypt (heir::lwe::RLWEDecryptOp)

Decrypt an RLWE ciphertext to a RLWE plaintext

Syntax:

operation ::= `lwe.rlwe_decrypt` operands attr-dict `:` functional-type(operands, results)

Decrypt an RLWE ciphertext to yield a RLWE plaintext

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputA ciphertext type
secret_keyA secret key for LWE

Results:

ResultDescription
outputA plaintext type

lwe.rlwe_encode (heir::lwe::RLWEEncodeOp)

Encode an integer to yield an RLWE plaintext

Syntax:

operation ::= `lwe.rlwe_encode` $input attr-dict `:` qualified(type($input)) `->` qualified(type($output))

Encode an integer to yield an RLWE plaintext.

This op uses a an encoding attribute to encode the bits of the integer into an RLWE plaintext value that can then be encrypted. CKKS cleartext inputs may be floating points, and a scaling factor described by the encoding will be applied.

Examples:

%Y = lwe.rlwe_encode %value {encoding = #enc, ring = #ring}: i1 to !lwe.rlwe_plaintext<encoding = #enc, ring = #ring>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
encoding::mlir::AttributeAn encoding of a scalar in the constant coefficient or An encoding of cleartexts directly as coefficients. or An encoding of cleartexts via the inverse canonical embedding. or An encoding of cleartexts via CRT slots.
ring::mlir::heir::polynomial::RingAttran attribute specifying a polynomial ring

Operands:

OperandDescription
inputsignless-integer-like or floating-point-like

Results:

ResultDescription
outputA plaintext type

lwe.rlwe_encrypt (heir::lwe::RLWEEncryptOp)

Encrypt an RLWE plaintext to a RLWE ciphertext

Syntax:

operation ::= `lwe.rlwe_encrypt` operands attr-dict `:` functional-type(operands, results)

Encrypt an RLWE plaintext to yield a RLWE ciphertext.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputA plaintext type
keyA secret key for LWE or A public key for LWE

Results:

ResultDescription
outputA ciphertext type

lwe.rmul (heir::lwe::RMulOp)

Multiplies two RLWE ciphertexts

Syntax:

operation ::= `lwe.rmul` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.rmul_plain (heir::lwe::RMulPlainOp)

Multiplication between RLWE ciphertext-plaintext

Syntax:

operation ::= `lwe.rmul_plain` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, InferTypeOpAdaptor, IsCiphertextPlaintextOp

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.rnegate (heir::lwe::RNegateOp)

Negate a RLWE ciphertexts

Syntax:

operation ::= `lwe.rnegate` operands attr-dict `:` type($output)

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.rsub (heir::lwe::RSubOp)

Subtract two RLWE ciphertexts

Syntax:

operation ::= `lwe.rsub` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Elementwise, InferTypeOpAdaptor, SameOperandsAndResultPlaintextTypes, SameOperandsAndResultRings, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-ciphertext-like
rhslwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.rsub_plain (heir::lwe::RSubPlainOp)

Subtraction between RLWE ciphertext-plaintext

Syntax:

operation ::= `lwe.rsub_plain` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor, IsCiphertextPlaintextOp, SameOperandsAndResultPlaintextTypes

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhslwe-plaintext-or-ciphertext-like
rhslwe-plaintext-or-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

lwe.trivial_encrypt (heir::lwe::TrivialEncryptOp)

Create a trivial encryption of a plaintext.

Syntax:

operation ::= `lwe.trivial_encrypt` $input attr-dict `:`  qualified(type(operands)) `to` qualified(type(results))

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
ciphertext_bits::mlir::IntegerAttrindex attribute

Operands:

OperandDescription
inputA plaintext type

Results:

ResultDescription
outputA ciphertext type

lwe.reinterpret_application_data (heir::lwe::ReinterpretApplicationDataOp)

A placeholder cast from one ciphertext type to another

Syntax:

operation ::= `lwe.reinterpret_application_data` $input attr-dict `:` qualified(type($input)) `to` qualified(type($output))

The cast op is thus used to translate application data (e.g., message_type) between ciphertexts in particular situations, such as when the bitwidth of the message type changes, but this change is not observed in the plaintext space, or when lowering to an API that does not keep track of types.

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputlwe-ciphertext-like

Results:

ResultDescription
outputlwe-ciphertext-like

LWE additional definitions

LweEncryptionType

An enum attribute representing an encryption method

Cases:

SymbolValueString
msb0msb
lsb1lsb
mix2mix

7.9 - MathExt

‘math_ext’ Dialect

Math-related operations we require for HEIR which do not (yet) exist in upstream math.

MathExt ops

math_ext.sign (heir::math_ext::SignOp)

Returns the sign of the input value

Syntax:

operation ::= `math_ext.sign` $value attr-dict `:` type($result)

Returns -1 if the input is negative, 0 if it is zero, and 1 if it is positive. The behavior is undefined for NaN inputs.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
valuesignless-integer-like or floating-point-like

Results:

ResultDescription
resultsignless-integer-like or floating-point-like

7.10 - Mgmt

‘mgmt’ Dialect

The mgmt dialect contains scheme-agnostic ciphertext management ops (like relinearize and mod reduce), to enable initial high-level compiler passes to perform a first pass at parameter selection, while lower-level passes may refine them with scheme-specific information.

Mgmt attributes

MgmtAttr

Container attribute for all mgmt parameter

Syntax:

#mgmt.mgmt<
  int,   # level
  int,   # dimension
  int64_t   # scale
>

This attribute is used to store all mgmt parameters.

The attribute is a struct with the following fields:

  • level : the level of the ciphertext, from L to 0
  • dimension : the dimension of the ciphertext, defaults to 2

Internally, this attribute is used by secret-to- for determining the level and dimension of the ciphertext.

It should be populated by –secret-with-mgmt- before going through the secret-to- pass.

Example:

#mgmt = #mgmt.mgmt<level = 1> // dimension defaults to 2
#mgmt1 = #mgmt.mgmt<level = 1, dimension = 3>
%0 = secret.generic(%arg0, %arg1 : !secret.secret<i16>) attrs = {mgmt.mgmt = #mgmt} {
   ...
} -> !secret.secret<i16>

Parameters:

ParameterC++ typeDescription
levelint
dimensionint
scaleint64_t

OpenfheParamsAttr

Container attribute for some OpenFHE-specific parameters

Syntax:

#mgmt.openfhe_params<
  int,   # evalAddCount
  int   # keySwitchCount
>

This attribute is used to store some OpenFHE-specific parameters.

The attribute is a struct with the following fields:

  • evalAddCount : param for OpenFHE SetEvalAddCount
  • keySwitchCount : param for OpenFHE SetKeySwitchCount

When this attribute presents, the lowering of openfhe pass will use these parameters to set the corresponding OpenFHE parameters.

It should be populated by –secret-with-mgmt-bgv before going through the secret-to-bgv bgv-to-openfhe pass.

Example:

#openfhe_params = #mgmt.openfhe_params<evalAddCount = 1, keySwitchCount = 1>

Parameters:

ParameterC++ typeDescription
evalAddCountint
keySwitchCountint

Mgmt ops

mgmt.adjust_scale (heir::mgmt::AdjustScaleOp)

Adjust the scale of the input ciphertext (for BGV and CKKS)

Syntax:

operation ::= `mgmt.adjust_scale` operands attr-dict `:` type($output)

This is scheme-agonistic operation that adjust the scale of the input ciphertext. This is an opaque operation, and the concrete value of the scale is determined by other methods.

To distinguish different opaque adjust_scale operations, the id attribute is used.

At the time of secret-insert-mgmt-<scheme>, the concrete scale is not known as the scheme parameter is not generated. Further passes like populate-scale-<scheme> is responsible for materializing the concrete scale when the scheme parameter is known.

When further lowered, it could be lowered to bgv.mul_plain or ckks.mul_plain depending on the scheme.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
id::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
inputany type

Results:

ResultDescription
outputany type

mgmt.bootstrap (heir::mgmt::BootstrapOp)

Bootstrap the input ciphertext to refresh its noise budget

Syntax:

operation ::= `mgmt.bootstrap` operands attr-dict `:` type($output)

This is a scheme-agnostic operation that implies bootstrapping of the input ciphertext to refresh its noise budget.

Bootstrapping is a technique used in homomorphic encryption to reduce the noise in a ciphertext, allowing further operations to be performed on it without decryption.

When further lowered, it could be lowered to bgv.bootstrap or ckks.bootstrap depending on the scheme.

For the current backend, only ckks.bootstrap is supported. Further backend may include bgv.bootstrap.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputany type

Results:

ResultDescription
outputany type

mgmt.init (heir::mgmt::InitOp)

Init the plaintext with mgmt attributes

Syntax:

operation ::= `mgmt.init` operands attr-dict `:` type($output)

This is a scheme-agnostic operation that initializes the plaintext with mgmt attributes.

Plaintext has multiple sources, e.g. function argument, arith.constant, tensor.empty, etc. However, they may have multiple uses in HE circuit and the level/scale information for them may be different, so we could not annotate them with mgmt attributes directly, as they could not have more than one annotation.

Also, mgmt attributes annotated on them may get lost as other optimization like CSE or constant folding may canonicalize them away.

To address the problem, for each use of the plaintext, we insert an mgmt.init operation to initialize the plaintext with mgmt attributes.

Technical reasons for registering memory effects:

Register a (bogus) memory effect to prevent CSE from merging this op. Two mgmt.init ops could be seen as equivalent only if they have the same MgmtAttr with level/dimension/scale annotated, otherwise we could not judge whether they are equivalent or not. In practice, we create the op first and only in later analyses we know whether they are equivalent or not.

ConditionallySpeculatable is for isSpeculatable check in hoisting canonicalization.

Traits: Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, MemoryEffectOpInterface (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{MemoryEffects::Write on ::mlir::SideEffects::DefaultResource}

Operands:

OperandDescription
inputany type

Results:

ResultDescription
outputany type

mgmt.level_reduce (heir::mgmt::LevelReduceOp)

Reduce the level of input ciphertext by dropping the last k RNS limbs

Syntax:

operation ::= `mgmt.level_reduce` operands attr-dict `:` type($output)

This scheme-agonistic operation reduces the ciphertext level by k, as specified by the levelToDrop attribute.

If levelToDrop is not specified, it defaults to 1.

Input ciphertext is assumed to be in RNS form when further lowered.

Later passes may lower this op to bgv.level_reduce or ckks.level_reduce depending on the scheme.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
levelToDrop::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
inputany type

Results:

ResultDescription
outputany type

mgmt.modreduce (heir::mgmt::ModReduceOp)

Modulus switch the input ciphertext down by one limb (RNS assumed)

Syntax:

operation ::= `mgmt.modreduce` operands attr-dict `:` type($output)

This is scheme-agonistic operation that implies modulus switching/rescaling by one limb.

Input ciphertext is assumed to be in RNS form when further lowered.

When further lowered, it could be lowered to bgv.modulus_switch or ckks.rescale depending on the scheme.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputany type

Results:

ResultDescription
outputany type

mgmt.relinearize (heir::mgmt::RelinearizeOp)

Relinearize the input ciphertext to be linear

Syntax:

operation ::= `mgmt.relinearize` operands attr-dict `:` type($output)

This is scheme-agonistic operation that implies relinearization of the input ciphertext to be linear (i.e. returns to dimension 2).

This is used solely by multiplication. For rotation, currently HEIR assumes relinearization is done internally and does not have a separate scheme-specific operation for it.

This accepts a ciphertext with dimension > 2 and returns a ciphertext with dimension 2. Note that the semantic includes the relinearization of higher dimension input like input with dimension 4 or higher, which when materialized should require multiple relinearization keys.

When further lowered, it could be lowered to bgv.relinearize or ckks.relinearize depending on the scheme.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputany type

Results:

ResultDescription
outputany type

7.11 - ModArith

‘mod_arith’ Dialect

The mod_arith dialect contains operations used for modulo arithmetic.

ModArith types

ModArithType

Integer type with modular arithmetic

Syntax:

!mod_arith.int<
  ::mlir::IntegerAttr   # modulus
>

mod_arith.int<p> represents an element of the ring of integers modulo $p$. The modulus attribute is the ring modulus, and mod_arith operations lower to arith operations that produce results in the range [0, modulus), often called the canonical representative.

modulus is specified with an integer type suffix, for example, mod_arith.int<65537 : i32>. This corresponds to the storage type for the modulus, and is i64 by default.

It is required that the underlying integer type should be larger than twice the modulus (have one extra bit of storage space) to avoid signedness issues. For example, when modulus == 2 ** 32 - 1, the underlying type for the modulus should be at least i33, though i64 is a natural choice.

Passes may allow intermediate values that do not always produce a canonical representative in [0, modulus). For example, if the machine storage type is i64, but the modulus fits within an i32, a lowering could allow intermediate arithmetic values to grow to as large as an i64 before reducing them. However, all passes must ensure that values used outside the local scope (e.g., function return values or arguments to calls to linked functions) are appropriately reduced to the canonical representative. modulus is the modulus the arithmetic working with.

Examples:

!Zp1 = !mod_arith.int<7> // implicitly being i64
!Zp2 = !mod_arith.int<65537 : i32>
!Zp3 = !mod_arith.int<536903681 : i64>

Parameters:

ParameterC++ typeDescription
modulus::mlir::IntegerAttr

ModArith ops

mod_arith.add (heir::mod_arith::AddOp)

Modular addition operation

Syntax:

operation ::= `mod_arith.add` operands attr-dict `:` type($output)

Computes modular addition.

Unless otherwise specified, the operation assumes both inputs are canonical representatives and guarantees the output being canonical representative.

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsmod_arith_or_rns-like
rhsmod_arith_or_rns-like

Results:

ResultDescription
outputmod_arith_or_rns-like

mod_arith.barrett_reduce (heir::mod_arith::BarrettReduceOp)

Compute the first step of the Barrett reduction.

Syntax:

operation ::= `mod_arith.barrett_reduce` operands attr-dict `:` qualified(type($input))

Let $q$ denote a statically known modulus and $b = 4^{w}$, where $w$ is the smallest bit-width that contains the range $[0, q)$. The Barrett reduce operation computes barret_reduce x = x - floor(x * floor(b / q) / b) * q.

Given $0 <= x < q^2$, then this will compute $(x \mod q)$ or $(x \mod q) + q$.

Traits: SameOperandsAndResultType

Interfaces: InferTypeOpInterface

Attributes:

AttributeMLIR TypeDescription
modulus::mlir::IntegerAttrarbitrary integer attribute

Operands:

OperandDescription
inputsignless-integer

Results:

ResultDescription
outputsignless-integer

mod_arith.constant (heir::mod_arith::ConstantOp)

Define a constant value via an attribute.

Example:

%0 = mod_arith.constant 123 : !mod_arith.int<65537:i32>

Traits: AlwaysSpeculatableImplTrait, ConstantLike

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
value::mlir::TypedAttrTypedAttr instance

Results:

ResultDescription
outputmod_arith-like

mod_arith.encapsulate (heir::mod_arith::EncapsulateOp)

Encapsulate an integer into a mod_arith type

Syntax:

operation ::= `mod_arith.encapsulate` operands attr-dict `:` type($input) `->` type($output)

mod_arith.encapsulate converts the integer to be of mod_arith or RNS type.

Examples:

mod_arith.encapsulate %c0 : i32 -> mod_arith.int<65537 : i32>
mod_arith.encapsulate %c1 : i64 -> mod_arith.int<65537 : i64>
mod_arith.encapsulate %c2 : tensor<4x2xi32> -> tensor<4xrns.rns<mod_arith.int<5 : i32>, mod_arith.int<17 : i32>>>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputsignless-integer

Results:

ResultDescription
outputmod_arith_or_rns-like

mod_arith.extract (heir::mod_arith::ExtractOp)

Extract the integer stored inside mod_arith type

Syntax:

operation ::= `mod_arith.extract` operands attr-dict `:` type($input) `->` type($output)

mod_arith.extract extracts the integer inside the mod_arith or RNS type.

It is required that the bitwidth of the output (tensor of) integer type is the same as that of the storage type of the input mod_arith (or RNS) type.

Examples:

%m0 = mod_arith.encapsulate %c0 : i32 -> mod_arith.int<65537 : i32>
%m1 = mod_arith.encapsulate %c1 : i64 -> mod_arith.int<65537 : i64>
%m2 = mod_arith.encapsulate %c2 : tensor<4x2xi32> -> tensor<4xrns.rns<mod_arith.int<5 : i32>, mod_arith.int<17 : i32>>>
%c3 = mod_arith.extract %m0 : mod_arith.int<65537 : i32> -> i32
%c4 = mod_arith.extract %m1 : mod_arith.int<65537 : i64> -> i64
%c5 = mod_arith.extract %m2 : tensor<4xrns.rns<mod_arith.int<5 : i32>, mod_arith.int<17 : i32>>> -> tensor<4x2xi32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputmod_arith_or_rns-like

Results:

ResultDescription
outputsignless-integer

mod_arith.mac (heir::mod_arith::MacOp)

Modular multiplication-and-accumulation operation

Syntax:

operation ::= `mod_arith.mac` operands attr-dict `:` type($output)

mod_arith.mac x, y, z computes $(x * y) + z$

Unless otherwise specified, the operation assumes all inputs are canonical representatives and guarantees the output being canonical representative.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsmod_arith-like
rhsmod_arith-like
accmod_arith-like

Results:

ResultDescription
outputmod_arith-like

mod_arith.mod_switch (heir::mod_arith::ModSwitchOp)

Change the modulus of a mod_arith

Syntax:

operation ::= `mod_arith.mod_switch` $input attr-dict `:` type($input) `to` type($output)

The “mod_switch” operation performs either modulus switching (changing the modulus of a mod_arith type to a new value by reducing modulo the new modulus) or CRT decomposition/interpolation.

A CRT decomposition can handle switching from a mod_arith type to the RNS modulus when the modulus of the mod_arith type is equal to the product of the RNS modulus. If the modulus is less than the RNS modulus product, it treats the input as an element of the larger product space via an injection.

Examples:

mod_arith.mod_switch %c0 : mod_arith.int<65537 : i32> to mod_arith.int<65539 : i32>
mod_arith.mod_switch %c0 : mod_arith.int<65537 : i32> to mod_arith.int<257 : i32>
mod_arith.mod_switch %c0 : mod_arith.int<85 : i32> to rns.rns<mod_arith.int<5 : i32>, mod_arith.int<17 : i32>>
mod_arith.mod_switch %c0 : mod_arith.int<45 : i32> to rns.rns<mod_arith.int<5 : i32>, mod_arith.int<17 : i32>>
mod_arith.mod_switch %c0 : rns.rns<mod_arith.int<5 : i32>, mod_arith.int<17 : i32>> to mod_arith.int<85 : i32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputmod_arith_or_rns-like

Results:

ResultDescription
outputmod_arith_or_rns-like

mod_arith.mul (heir::mod_arith::MulOp)

Modular multiplication operation

Syntax:

operation ::= `mod_arith.mul` operands attr-dict `:` type($output)

Computes modular multiplication.

Unless otherwise specified, the operation assumes both inputs are canonical representatives and guarantees the output being canonical representative.

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsmod_arith_or_rns-like
rhsmod_arith_or_rns-like

Results:

ResultDescription
outputmod_arith_or_rns-like

mod_arith.reduce (heir::mod_arith::ReduceOp)

Reduce the mod arith type to its canonical representative

Syntax:

operation ::= `mod_arith.reduce` operands attr-dict `:` type($output)

mod_arith.reduce x produces $y$, the canonical representative in $[0, q)$ such that $x \equiv y \mod q$.

Examples:

%c0 = arith.constant 65538 : i32
%m0 = mod_arith.encapsulate %c0 : i32 -> mod_arith.int<65537 : i32>
// mod_arith.extract %m0 produces 65538
%m1 = mod_arith.reduce %m0 : mod_arith.int<65537: i32>
// mod_arith.extract %m1 produces 1

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputmod_arith-like

Results:

ResultDescription
outputmod_arith-like

mod_arith.subifge (heir::mod_arith::SubIfGEOp)

Compute (x >= y) ? x - y : x.

Syntax:

operation ::= `mod_arith.subifge` operands attr-dict `:` qualified(type($output))

Traits: SameOperandsAndResultType

Interfaces: InferTypeOpInterface

Operands:

OperandDescription
lhssignless-integer
rhssignless-integer

Results:

ResultDescription
outputsignless-integer

mod_arith.sub (heir::mod_arith::SubOp)

Modular subtraction operation

Syntax:

operation ::= `mod_arith.sub` operands attr-dict `:` type($output)

Computes modular subtraction.

Unless otherwise specified, the operation assumes both inputs are canonical representatives and guarantees the output being canonical representative.

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhsmod_arith_or_rns-like
rhsmod_arith_or_rns-like

Results:

ResultDescription
outputmod_arith_or_rns-like

7.12 - Openfhe

‘openfhe’ Dialect

The openfhe dialect is an exit dialect for generating c++ code against the OpenFHE library API.

See https://github.com/openfheorg/openfhe-development

Openfhe types

CCParamsType

The CCParams required to create CryptoContext.

Syntax: !openfhe.cc_params

CryptoContextType

The CryptoContext required to perform homomorphic operations in OpenFHE.

Syntax: !openfhe.crypto_context

DigitDecompositionType

A precomputed digit decomposition for for EvalFastRotation

Syntax: !openfhe.digit_decomp

EvalKeyType

The evaluation key required to keyswitch/relinearize/rotate/automorphism operation in OpenFHE.

Syntax: !openfhe.eval_key

PrivateKeyType

The private key required to decrypt a ciphertext in OpenFHE.

Syntax: !openfhe.private_key

PublicKeyType

The public key required to encrypt plaintext in OpenFHE.

Syntax: !openfhe.public_key

Openfhe ops

openfhe.add_inplace (heir::openfhe::AddInPlaceOp)

Performs in-place homomorphic addition, modifying lhs.

Syntax:

operation ::= `openfhe.add_inplace` operands attr-dict `:` functional-type(operands, results)

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
lhsA ciphertext type
rhsA ciphertext type

openfhe.add (heir::openfhe::AddOp)

OpenFHE add operation of two ciphertexts.

Syntax:

operation ::= `openfhe.add` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor, SameOperandsAndResultRings

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
lhsA ciphertext type
rhsA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.add_plain (heir::openfhe::AddPlainOp)

OpenFHE add operation of a ciphertext and a plaintext.

Syntax:

operation ::= `openfhe.add_plain` operands attr-dict `:` functional-type(operands, results)

Traits: AllCiphertextTypesMatch, AlwaysSpeculatableImplTrait, InferTypeOpAdaptor

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
lhsA ciphertext type or A plaintext type
rhsA ciphertext type or A plaintext type

Results:

ResultDescription
outputA ciphertext type

openfhe.automorph (heir::openfhe::AutomorphOp)

Syntax:

operation ::= `openfhe.automorph` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type
evalKeyThe evaluation key required to keyswitch/relinearize/rotate/automorphism operation in OpenFHE.

Results:

ResultDescription
outputA ciphertext type

openfhe.bootstrap (heir::openfhe::BootstrapOp)

OpenFHE bootstrap operation of a ciphertext. (For CKKS)

Syntax:

operation ::= `openfhe.bootstrap` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.decrypt (heir::openfhe::DecryptOp)

Syntax:

operation ::= `openfhe.decrypt` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type
privateKeyThe private key required to decrypt a ciphertext in OpenFHE.

Results:

ResultDescription
plaintextA plaintext type

openfhe.encrypt (heir::openfhe::EncryptOp)

Syntax:

operation ::= `openfhe.encrypt` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
plaintextA plaintext type
encryptionKeyThe public key required to encrypt plaintext in OpenFHE. or The private key required to decrypt a ciphertext in OpenFHE.

Results:

ResultDescription
ciphertextA ciphertext type

openfhe.fast_rotation (heir::openfhe::FastRotationOp)

Syntax:

operation ::= `openfhe.fast_rotation` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
index::mlir::IntegerAttrindex attribute
cyclotomicOrder::mlir::IntegerAttrindex attribute

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
inputA ciphertext type
precomputedDigitDecompA precomputed digit decomposition for for EvalFastRotation

Results:

ResultDescription
outputA ciphertext type

openfhe.fast_rotation_precompute (heir::openfhe::FastRotationPrecomputeOp)

Syntax:

operation ::= `openfhe.fast_rotation_precompute` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
inputA ciphertext type

Results:

ResultDescription
outputA precomputed digit decomposition for for EvalFastRotation

openfhe.gen_bootstrapkey (heir::openfhe::GenBootstrapKeyOp)

Syntax:

operation ::= `openfhe.gen_bootstrapkey` operands attr-dict `:` functional-type(operands, results)

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
privateKeyThe private key required to decrypt a ciphertext in OpenFHE.

openfhe.gen_context (heir::openfhe::GenContextOp)

Syntax:

operation ::= `openfhe.gen_context` operands attr-dict `:` functional-type(operands, results)

Interfaces: InferTypeOpInterface

Attributes:

AttributeMLIR TypeDescription
supportFHE::mlir::BoolAttrbool attribute

Operands:

OperandDescription
paramsThe CCParams required to create CryptoContext.

Results:

ResultDescription
contextThe CryptoContext required to perform homomorphic operations in OpenFHE.

openfhe.gen_mulkey (heir::openfhe::GenMulKeyOp)

Syntax:

operation ::= `openfhe.gen_mulkey` operands attr-dict `:` functional-type(operands, results)

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
privateKeyThe private key required to decrypt a ciphertext in OpenFHE.

openfhe.gen_params (heir::openfhe::GenParamsOp)

Syntax:

operation ::= `openfhe.gen_params` operands attr-dict `:` functional-type(operands, results)

Generates the parameters for the OpenFHE scheme.

mulDepth is the depth of the multiplication circuit, including the bootstrapping depth.

plainMod is the modulus of the plaintext space. If we are using CKKS, this is 0.

insecure is a flag that determines whether the parameters are generated securely or not. In Openfhe, this means setting HEStd_NotSet for security level.

For other flags, see the OpenFHE documentation in https://github.com/openfheorg/openfhe-development/blob/main/src/pke/examples/README.md#description-of-the-cryptocontext-parameters-and-their-restrictions

Interfaces: InferTypeOpInterface

Attributes:

AttributeMLIR TypeDescription
mulDepth::mlir::IntegerAttr64-bit signless integer attribute
plainMod::mlir::IntegerAttr64-bit signless integer attribute
ringDim::mlir::IntegerAttr64-bit signless integer attribute
batchSize::mlir::IntegerAttr64-bit signless integer attribute
firstModSize::mlir::IntegerAttr64-bit signless integer attribute
scalingModSize::mlir::IntegerAttr64-bit signless integer attribute
evalAddCount::mlir::IntegerAttr64-bit signless integer attribute
keySwitchCount::mlir::IntegerAttr64-bit signless integer attribute
digitSize::mlir::IntegerAttr64-bit signless integer attribute
numLargeDigits::mlir::IntegerAttr64-bit signless integer attribute
maxRelinSkDeg::mlir::IntegerAttr64-bit signless integer attribute
insecure::mlir::BoolAttrbool attribute
encryptionTechniqueExtended::mlir::BoolAttrbool attribute
keySwitchingTechniqueBV::mlir::BoolAttrbool attribute
scalingTechniqueFixedManual::mlir::BoolAttrbool attribute

Results:

ResultDescription
paramsThe CCParams required to create CryptoContext.

openfhe.gen_rotkey (heir::openfhe::GenRotKeyOp)

Syntax:

operation ::= `openfhe.gen_rotkey` operands attr-dict `:` functional-type(operands, results)

Attributes:

AttributeMLIR TypeDescription
indices::mlir::DenseI64ArrayAttri64 dense array attribute

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
privateKeyThe private key required to decrypt a ciphertext in OpenFHE.

openfhe.key_switch (heir::openfhe::KeySwitchOp)

Syntax:

operation ::= `openfhe.key_switch` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type
evalKeyThe evaluation key required to keyswitch/relinearize/rotate/automorphism operation in OpenFHE.

Results:

ResultDescription
outputA ciphertext type

openfhe.level_reduce (heir::openfhe::LevelReduceOp)

OpenFHE level_reduce operation of a ciphertext.

Syntax:

operation ::= `openfhe.level_reduce` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
levelToDrop::mlir::IntegerAttr64-bit signless integer attribute

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.make_ckks_packed_plaintext (heir::openfhe::MakeCKKSPackedPlaintextOp)

Syntax:

operation ::= `openfhe.make_ckks_packed_plaintext` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
valueranked tensor of floating-point or integer values

Results:

ResultDescription
plaintextA plaintext type

openfhe.make_packed_plaintext (heir::openfhe::MakePackedPlaintextOp)

Syntax:

operation ::= `openfhe.make_packed_plaintext` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
valueranked tensor of integer values

Results:

ResultDescription
plaintextA plaintext type

openfhe.mod_reduce (heir::openfhe::ModReduceOp)

OpenFHE mod_reduce operation of a ciphertext. (used only for BGV/CKKS)

Syntax:

operation ::= `openfhe.mod_reduce` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.mul_const (heir::openfhe::MulConstOp)

OpenFHE mul operation of a ciphertext and a constant.

Syntax:

operation ::= `openfhe.mul_const` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type
constant64-bit signless integer

Results:

ResultDescription
outputA ciphertext type

openfhe.mul_no_relin (heir::openfhe::MulNoRelinOp)

OpenFHE mul operation of two ciphertexts without relinearization.

Syntax:

operation ::= `openfhe.mul_no_relin` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor, SameOperandsAndResultRings

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
lhsA ciphertext type
rhsA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.mul (heir::openfhe::MulOp)

OpenFHE mul operation of two ciphertexts with relinearization.

Syntax:

operation ::= `openfhe.mul` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
lhsA ciphertext type
rhsA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.mul_plain (heir::openfhe::MulPlainOp)

OpenFHE mul operation of a ciphertext and a plaintext.

Syntax:

operation ::= `openfhe.mul_plain` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type
plaintextA plaintext type

Results:

ResultDescription
outputA ciphertext type

openfhe.negate (heir::openfhe::NegateOp)

OpenFHE negate operation of a ciphertext.

Syntax:

operation ::= `openfhe.negate` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.relin (heir::openfhe::RelinOp)

OpenFHE relinearize operation of a ciphertext.

Syntax:

operation ::= `openfhe.relin` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.rot (heir::openfhe::RotOp)

Syntax:

operation ::= `openfhe.rot` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
index::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.setup_bootstrap (heir::openfhe::SetupBootstrapOp)

Syntax:

operation ::= `openfhe.setup_bootstrap` operands attr-dict `:` functional-type(operands, results)

Attributes:

AttributeMLIR TypeDescription
levelBudgetEncode::mlir::IntegerAttrAn Attribute containing a integer value
levelBudgetDecode::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.

openfhe.square (heir::openfhe::SquareOp)

OpenFHE square operation of a ciphertext.

Syntax:

operation ::= `openfhe.square` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
ciphertextA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.sub_inplace (heir::openfhe::SubInPlaceOp)

Performs in-place homomorphic subtraction, modifying lhs.

Syntax:

operation ::= `openfhe.sub_inplace` operands attr-dict `:` functional-type(operands, results)

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
lhsA ciphertext type
rhsA ciphertext type

openfhe.sub (heir::openfhe::SubOp)

OpenFHE sub operation of two ciphertexts.

Syntax:

operation ::= `openfhe.sub` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor, SameOperandsAndResultRings

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
lhsA ciphertext type
rhsA ciphertext type

Results:

ResultDescription
outputA ciphertext type

openfhe.sub_plain (heir::openfhe::SubPlainOp)

OpenFHE sub operation of a ciphertext and a plaintext.

Syntax:

operation ::= `openfhe.sub_plain` operands attr-dict `:` functional-type(operands, results)

Traits: AllCiphertextTypesMatch, AlwaysSpeculatableImplTrait, InferTypeOpAdaptor

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cryptoContextThe CryptoContext required to perform homomorphic operations in OpenFHE.
lhsA ciphertext type or A plaintext type
rhsA ciphertext type or A plaintext type

Results:

ResultDescription
outputA ciphertext type

7.13 - Orion

‘orion’ Dialect

The orion dialect is an entry dialect for the Orion compiler into the heir ecosystem. It is primarily intended to enable comparisons between Orion and HEIR.

Because an existing translator was written that converts from Orion to HEIR’s CKKS dialect, this dialect serves to include the ops not supported by the CKKS dialect, but which are expressed as black boxes by Orion.

Orion ops

orion.chebyshev (heir::orion::ChebyshevOp)

Evaluates a Chebyshev polynomial on a ciphertext using pre-computed coefficients

Syntax:

operation ::= `orion.chebyshev` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
coefficients::mlir::ArrayAttrarray attribute
domain_start::mlir::FloatAttrAn Attribute containing a floating-point value
domain_end::mlir::FloatAttrAn Attribute containing a floating-point value

Operands:

OperandDescription
inputA ciphertext type

Results:

ResultDescription
resultA ciphertext type

orion.linear_transform (heir::orion::LinearTransformOp)

Apply a linear transformation to the input ciphertext using pre-computed diagonals

Syntax:

operation ::= `orion.linear_transform` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputA ciphertext type
diagonalsfloating-point-like

Results:

ResultDescription
resultA ciphertext type

7.14 - Polynomial

‘polynomial’ Dialect

The Polynomial dialect defines single-variable polynomial types and operations.

The simplest use of polynomial is to represent mathematical operations in a polynomial ring R[x], where R is another MLIR type like i32.

More generally, this dialect supports representing polynomial operations in a quotient ring R[X]/(f(x)) for some statically fixed polynomial f(x). Two polyomials p(x), q(x) are considered equal in this ring if they have the same remainder when dividing by f(x). When a modulus is given, ring operations are performed with reductions modulo f(x) and relative to the coefficient ring R.

Examples:

// A constant polynomial in a ring with i32 coefficients and no polynomial modulus
#ring = #polynomial.ring<coefficientType=i32>
%a = polynomial.constant <1 + x**2 - 3x**3> : polynomial.polynomial<#ring>

// A constant polynomial in a ring with i32 coefficients, modulo (x^1024 + 1)
#modulus = #polynomial.int_polynomial<1 + x**1024>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#modulus>
%a = polynomial.constant <1 + x**2 - 3x**3> : polynomial.polynomial<#ring>

// A constant polynomial in a ring with i32 coefficients, with a polynomial
// modulus of (x^1024 + 1) and a coefficient modulus of 17.
#modulus = #polynomial.int_polynomial<1 + x**1024>
!coeff_ty = !mod_arith.int<17 : i32>
#ring = #polynomial.ring<coefficientType=!coeff_ty, polynomialModulus=#modulus>
%a = polynomial.constant <1 + x**2 - 3x**3> : polynomial.polynomial<#ring>

Polynomial attributes

ChebyshevPolynomialAttr

An attribute containing a single-variable polynomial with float coefficients in the Chebyshev basis

Syntax:

#polynomial.chebyshev_polynomial<
  ArrayAttr   # coefficients
>

This attribute represents a single-variable polynomial with double precision floating point coefficients, represented in the basis of Chebyshev polynomials of the first kind.

Example:

#poly = #polynomial.chebyshev_polynomial<[1.0, 2.0, 3.0, 4.0]>

Parameters:

ParameterC++ typeDescription
coefficientsArrayAttr

FloatPolynomialAttr

An attribute containing a single-variable polynomial with double precision floating point coefficients

A polynomial attribute represents a single-variable polynomial with double precision floating point coefficients.

The polynomial must be expressed as a list of monomial terms, with addition or subtraction between them. The choice of variable name is arbitrary, but must be consistent across all the monomials used to define a single attribute. The order of monomial terms is arbitrary, each monomial degree must occur at most once.

Example:

#poly = #polynomial.float_polynomial<0.5 x**7 + 1.5>

Parameters:

ParameterC++ typeDescription
polynomialFloatPolynomial

IntPolynomialAttr

An attribute containing a single-variable polynomial with integer coefficients

A polynomial attribute represents a single-variable polynomial with integer coefficients, which is used to define the modulus of a RingAttr, as well as to define constants and perform constant folding for polynomial ops.

The polynomial must be expressed as a list of monomial terms, with addition or subtraction between them. The choice of variable name is arbitrary, but must be consistent across all the monomials used to define a single attribute. The order of monomial terms is arbitrary, each monomial degree must occur at most once.

Example:

#poly = #polynomial.int_polynomial<x**1024 + 1>

Parameters:

ParameterC++ typeDescription
polynomial::mlir::heir::polynomial::IntPolynomial

PrimitiveRootAttr

An attribute containing an integer and its degree as a root of unity

Syntax:

#polynomial.primitive_root<
  ::mlir::IntegerAttr,   # value
  ::mlir::IntegerAttr   # degree
>

A primitive root attribute stores an integer root value and an integer degree, corresponding to a primitive root of unity of the given degree in an unspecified ring.

This is used as an attribute on polynomial.ntt and polynomial.intt ops to specify the root of unity used in lowering the transform.

Example:

#poly = #polynomial.primitive_root<value=123 : i32, degree : 7 index>

Parameters:

ParameterC++ typeDescription
value::mlir::IntegerAttr
degree::mlir::IntegerAttr

RingAttr

An attribute specifying a polynomial ring

Syntax:

#polynomial.ring<
  Type,   # coefficientType
  ::mlir::heir::polynomial::IntPolynomialAttr   # polynomialModulus
>

A ring describes the domain in which polynomial arithmetic occurs. The ring attribute in polynomial represents the more specific case of polynomials with a single indeterminate; whose coefficients can be represented by another MLIR type (coefficientType).

All semantics pertaining to arithmetic in the ring must be owned by the coefficient type. For example, if the polynomials are with integer coefficients taken modulo a prime $p$, then coefficientType must be a type that represents integers modulo $p$, such as mod_arith<p>.

Additionally, a polynomial ring may specify a polynomialModulus, which converts polynomial arithmetic to the analogue of modular integer arithmetic, where each polynomial is represented as its remainder when dividing by the modulus. For single-variable polynomials, a polynomial modulus is always specified via a single polynomial.

An expressive example is polynomials with i32 coefficients, whose coefficients are taken modulo 2**32 - 5, with a polynomial modulus of x**1024 - 1.

#poly_mod = #polynomial.int_polynomial<-1 + x**1024>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly_mod>

%0 = ... : polynomial.polynomial<#ring>

In this case, the value of a polynomial is always “converted” to a canonical form by applying repeated reductions by setting x**1024 = 1 and simplifying.

Parameters:

ParameterC++ typeDescription
coefficientTypeType
polynomialModulus::mlir::heir::polynomial::IntPolynomialAttr

TypedChebyshevPolynomialAttr

A typed chebyshev_polynomial

Syntax:

#polynomial.typed_chebyshev_polynomial<
  ::mlir::Type,   # type
  ::mlir::heir::polynomial::ChebyshevPolynomialAttr   # value
>

Example:

!poly_ty = !polynomial.polynomial<ring=<coefficientType=f32>>
#poly = float<1.4 x**7 + 4.5> : !poly_ty
#poly_verbose = #polynomial.typed_chebyshev_polynomial<[1.4, 4.5, 6.0, 7.0]> : !poly_ty

Parameters:

ParameterC++ typeDescription
type::mlir::Type
value::mlir::heir::polynomial::ChebyshevPolynomialAttr

TypedFloatPolynomialAttr

A typed float_polynomial

Syntax:

#polynomial.typed_float_polynomial<
  ::mlir::Type,   # type
  ::mlir::heir::polynomial::FloatPolynomialAttr   # value
>

Example:

!poly_ty = !polynomial.polynomial<ring=<coefficientType=f32>>
#poly = float<1.4 x**7 + 4.5> : !poly_ty
#poly_verbose = #polynomial.typed_float_polynomial<1.4 x**7 + 4.5> : !poly_ty

Parameters:

ParameterC++ typeDescription
type::mlir::Type
value::mlir::heir::polynomial::FloatPolynomialAttr

TypedIntPolynomialAttr

A typed int_polynomial

Syntax:

#polynomial.typed_int_polynomial<
  ::mlir::Type,   # type
  ::mlir::heir::polynomial::IntPolynomialAttr   # value
>

Example:

!poly_ty = !polynomial.polynomial<ring=<coefficientType=i32>>
#poly = int<1 x**7 + 4> : !poly_ty
#poly_verbose = #polynomial.typed_int_polynomial<1 x**7 + 4> : !poly_ty

Parameters:

ParameterC++ typeDescription
type::mlir::Type
value::mlir::heir::polynomial::IntPolynomialAttr

Polynomial types

PolynomialType

An element of a polynomial ring.

Syntax:

!polynomial.polynomial<
  ::mlir::heir::polynomial::RingAttr   # ring
>

A type for polynomials in a polynomial quotient ring.

Parameters:

ParameterC++ typeDescription
ring::mlir::heir::polynomial::RingAttran attribute specifying a polynomial ring

Polynomial ops

polynomial.add (heir::polynomial::AddOp)

Addition operation between polynomials.

Syntax:

operation ::= `polynomial.add` operands attr-dict `:` type($result)

Performs polynomial addition on the operands. The operands may be single polynomials or containers of identically-typed polynomials, i.e., polynomials from the same underlying ring with the same coefficient types.

This op is defined to occur in the ring defined by the ring attribute of the two operands, meaning the arithmetic is taken modulo the polynomialModulus of the ring as well as modulo any semantics defined by the coefficient type.

Example:

// add two polynomials modulo x^1024 - 1
#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
%0 = polynomial.constant int<1 + x**2> : !polynomial.polynomial<#ring>
%1 = polynomial.constant int<x**5 - x + 1> : !polynomial.polynomial<#ring>
%2 = polynomial.add %0, %1 : !polynomial.polynomial<#ring>

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhspolynomial-like
rhspolynomial-like

Results:

ResultDescription
resultpolynomial-like

polynomial.constant (heir::polynomial::ConstantOp)

Define a constant polynomial via an attribute.

Example:

!int_poly_ty = !polynomial.polynomial<ring=<coefficientType=i32>>
%0 = polynomial.constant int<1 + x**2> : !int_poly_ty

!float_poly_ty = !polynomial.polynomial<ring=<coefficientType=f32>>
%1 = polynomial.constant float<0.5 + 1.3e06 x**2> : !float_poly_ty

Traits: AlwaysSpeculatableImplTrait, InferTypeOpAdaptor

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
value::mlir::Attributea typed float_polynomial or a typed int_polynomial or a typed chebyshev_polynomial

Results:

ResultDescription
outputAn element of a polynomial ring.

polynomial.eval (heir::polynomial::EvalOp)

Evaluate a static polynomial attribute at a given SSA value.

Syntax:

operation ::= `polynomial.eval` $polynomial `,` $value attr-dict `:` type($value)

Evaluates the result of a polynomial specified as a static attribute at a given SSA value. The result represents the evaluation of the polynomial at the input value and produces a corresponding scalar value.

Example:

!poly_ty = !polynomial.polynomial<ring=<coefficientType=i32>>
#poly = #polynomial.typed_int_polynomial<1 + x + x**2> : !poly_ty
%x = arith.constant 5 : i32
%result = polynomial.eval #poly, %x : i32

The coefficient type of the polynomial does not necessarily need to be the same as the scalar input type. For example, one may evaluate a square matrix in a polynomial, because the scalar-matrix operation is well-defined. It is the responsibility of the lowering to determine if the input is compatible with the polynomial coefficient type.

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
polynomial::mlir::Attributea typed float_polynomial or a typed int_polynomial or a typed chebyshev_polynomial

Operands:

OperandDescription
valueany type

Results:

ResultDescription
outputany type

polynomial.from_tensor (heir::polynomial::FromTensorOp)

Creates a polynomial from integer coefficients stored in a tensor.

Syntax:

operation ::= `polynomial.from_tensor` $input attr-dict `:` type($input) `->` type($output)

polynomial.from_tensor creates a polynomial value from a tensor of coefficients. The input tensor must list the coefficients in degree-increasing order.

The input one-dimensional tensor may have size at most the degree of the ring’s polynomialModulus generator polynomial, with smaller dimension implying that all higher-degree terms have coefficient zero.

Example:

#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
%two = arith.constant 2 : i32
%five = arith.constant 5 : i32
%coeffs = tensor.from_elements %two, %two, %five : tensor<3xi32>
%poly = polynomial.from_tensor %coeffs : tensor<3xi32> -> !polynomial.polynomial<#ring>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputranked tensor of any type values

Results:

ResultDescription
outputAn element of a polynomial ring.

polynomial.intt (heir::polynomial::INTTOp)

Computes the reverse integer Number Theoretic Transform (NTT).

Syntax:

operation ::= `polynomial.intt` $input attr-dict `:` qualified(type($input)) `->` type($output)

polynomial.intt computes the reverse integer Number Theoretic Transform (INTT) on the input tensor. This is the inverse operation of the polynomial.ntt operation.

The input tensor is interpreted as a point-value representation of the output polynomial at powers of a primitive n-th root of unity (see polynomial.ntt). The ring of the polynomial is taken from the required encoding attribute of the tensor.

The choice of primitive root may be optionally specified.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
root::mlir::heir::polynomial::PrimitiveRootAttran attribute containing an integer and its degree as a root of unity

Operands:

OperandDescription
inputranked tensor of Integer type with modular arithmetic values

Results:

ResultDescription
outputAn element of a polynomial ring.

polynomial.key_switch_inner (heir::polynomial::KeySwitchInnerOp)

Key switch on an RNS polynomial component

Syntax:

operation ::= `polynomial.key_switch_inner` operands attr-dict `:` functional-type(operands, results)

Generates a linear ciphertext that, when added to a ciphertext encrypted under the input key, switches it to a ciphertext encrypted under the output key.

This operation is intended to be an internal implementation detail of higher-level ciphertext operations such as ckks.relinearize, isolated here for reuse among multiple op lowerings.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
valueAn element of a polynomial ring.
keySwitchingKeyranked tensor of An element of a polynomial ring. values

Results:

ResultDescription
constantOutputAn element of a polynomial ring.
linearOutputAn element of a polynomial ring.

polynomial.leading_term (heir::polynomial::LeadingTermOp)

Compute the leading term of the polynomial.

Syntax:

operation ::= `polynomial.leading_term` operands attr-dict `:` type($input) `->` `(` type($degree) `,` type($coefficient) `)`

The degree of a polynomial is the largest $k$ for which the coefficient a_k of x^k is nonzero. The leading term is the term a_k * x^k, which this op represents as a pair of results. The first is the degree k as an index, and the second is the coefficient, whose type matches the coefficient type of the polynomial’s ring attribute.

Example:

#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
%0 = polynomial.constant int<1 + x**2> : !polynomial.polynomial<#ring>
%1, %2 = polynomial.leading_term %0 : !polynomial.polynomial<#ring> -> (index, i32)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputAn element of a polynomial ring.

Results:

ResultDescription
degreeindex
coefficientany type

polynomial.mod_switch (heir::polynomial::ModSwitchOp)

Change the coefficient type of a polynomial.

Syntax:

operation ::= `polynomial.mod_switch` $input attr-dict `:` type($input) `to` type($output)

polynomial.mod_switch changes the coefficient type of a polynomial.

The two polynomials must have the same polynomialModulus.

Example:

#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring32 = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
#ring64 = #polynomial.ring<coefficientType=i64, polynomialModulus=#poly>
%poly = polynomial.mod_switch %coeffs : !polynomial.polynomial<#ring64> to !polynomial.polynomial<#ring32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputAn element of a polynomial ring.

Results:

ResultDescription
outputAn element of a polynomial ring.

polynomial.monic_monomial_mul (heir::polynomial::MonicMonomialMulOp)

Multiply a polynomial by a monic monomial.

Syntax:

operation ::= `polynomial.monic_monomial_mul` operands attr-dict `:` functional-type(operands, results)

Multiply a polynomial by a monic monomial, meaning a polynomial of the form 1 * x^k for an index operand k.

In some special rings of polynomials, such as a ring of polynomials modulo x^n - 1, monomial_mul can be interpreted as a cyclic shift of the coefficients of the polynomial. For some rings, this results in optimized lowerings that involve rotations and rescaling of the coefficients of the input.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputpolynomial-like
monomialDegreeindex

Results:

ResultDescription
outputpolynomial-like

polynomial.monomial (heir::polynomial::MonomialOp)

Create a polynomial that consists of a single monomial.

Syntax:

operation ::= `polynomial.monomial` operands attr-dict `:` functional-type(operands, results)

Construct a polynomial that consists of a single monomial term, from its degree and coefficient as dynamic inputs.

The coefficient type of the output polynomial’s ring attribute must match the coefficient input type.

Example:

#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
%deg = arith.constant 1023 : index
%five = arith.constant 5 : i32
%0 = polynomial.monomial %five, %deg : (i32, index) -> !polynomial.polynomial<#ring>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
coefficientany type
degreeindex

Results:

ResultDescription
outputAn element of a polynomial ring.

polynomial.mul (heir::polynomial::MulOp)

Multiplication operation between polynomials.

Syntax:

operation ::= `polynomial.mul` operands attr-dict `:` type($result)

Performs polynomial multiplication on the operands. The operands may be single polynomials or containers of identically-typed polynomials, i.e., polynomials from the same underlying ring with the same coefficient types.

This op is defined to occur in the ring defined by the ring attribute of the two operands, meaning the arithmetic is taken modulo the polynomialModulus of the ring as well as modulo any semantics defined by the coefficient type.

Example:

// multiply two polynomials modulo x^1024 - 1
#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
%0 = polynomial.constant int<1 + x**2> : !polynomial.polynomial<#ring>
%1 = polynomial.constant int<x**5 - x + 1> : !polynomial.polynomial<#ring>
%2 = polynomial.mul %0, %1 : !polynomial.polynomial<#ring>

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhspolynomial-like
rhspolynomial-like

Results:

ResultDescription
resultpolynomial-like

polynomial.mul_scalar (heir::polynomial::MulScalarOp)

Multiplication by a scalar of the field.

Syntax:

operation ::= `polynomial.mul_scalar` operands attr-dict `:` type($polynomial) `,` type($scalar)

Multiplies the polynomial operand’s coefficients by a given scalar value. The scalar input must have the same type as the polynomial ring’s coefficientType.

Example:

// multiply two polynomials modulo x^1024 - 1
#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
%0 = polynomial.constant int<1 + x**2> : !polynomial.polynomial<#ring>
%1 = arith.constant 3 : i32
%2 = polynomial.mul_scalar %0, %1 : !polynomial.polynomial<#ring>, i32

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
polynomialpolynomial-like
scalarany type

Results:

ResultDescription
outputpolynomial-like

polynomial.ntt (heir::polynomial::NTTOp)

Computes point-value tensor representation of a polynomial.

Syntax:

operation ::= `polynomial.ntt` $input attr-dict `:` qualified(type($input)) `->` type($output)

polynomial.ntt computes the forward integer Number Theoretic Transform (NTT) on the input polynomial. It returns a tensor containing a point-value representation of the input polynomial. The output tensor has shape equal to the degree of the ring’s polynomialModulus. The polynomial’s RingAttr is embedded as the encoding attribute of the output tensor.

Given an input polynomial F(x) over a ring whose polynomialModulus has degree n, and a primitive n-th root of unity omega_n, the output is the list of $n$ evaluations

f[k] = F(omega[n]^k) ; k = {0, ..., n-1}

The choice of primitive root may be optionally specified.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
root::mlir::heir::polynomial::PrimitiveRootAttran attribute containing an integer and its degree as a root of unity

Operands:

OperandDescription
inputAn element of a polynomial ring.

Results:

ResultDescription
outputranked tensor of Integer type with modular arithmetic values

polynomial.sub (heir::polynomial::SubOp)

Subtraction operation between polynomials.

Syntax:

operation ::= `polynomial.sub` operands attr-dict `:` type($result)

Performs polynomial subtraction on the operands. The operands may be single polynomials or containers of identically-typed polynomials, i.e., polynomials from the same underlying ring with the same coefficient types.

This op is defined to occur in the ring defined by the ring attribute of the two operands, meaning the arithmetic is taken modulo the polynomialModulus of the ring as well as modulo any semantics defined by the coefficient type.

Example:

// subtract two polynomials modulo x^1024 - 1
#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
%0 = polynomial.constant int<1 + x**2> : !polynomial.polynomial<#ring>
%1 = polynomial.constant int<x**5 - x + 1> : !polynomial.polynomial<#ring>
%2 = polynomial.sub %0, %1 : !polynomial.polynomial<#ring>

Traits: AlwaysSpeculatableImplTrait, Elementwise, SameOperandsAndResultType, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
lhspolynomial-like
rhspolynomial-like

Results:

ResultDescription
resultpolynomial-like

polynomial.to_tensor (heir::polynomial::ToTensorOp)

Creates a tensor containing the coefficients of a polynomial.

Syntax:

operation ::= `polynomial.to_tensor` $input attr-dict `:` type($input) `->` type($output)

polynomial.to_tensor creates a dense tensor value containing the coefficients of the input polynomial. The output tensor contains the coefficients in degree-increasing order.

Operations that act on the coefficients of a polynomial, such as extracting a specific coefficient or extracting a range of coefficients, should be implemented by composing to_tensor with the relevant tensor dialect ops.

The output tensor has shape equal to the degree of the polynomial ring attribute’s polynomialModulus, including zeroes.

Example:

#poly = #polynomial.int_polynomial<x**1024 - 1>
#ring = #polynomial.ring<coefficientType=i32, polynomialModulus=#poly>
%two = arith.constant 2 : i32
%five = arith.constant 5 : i32
%coeffs = tensor.from_elements %two, %two, %five : tensor<3xi32>
%poly = polynomial.from_tensor %coeffs : tensor<3xi32> -> !polynomial.polynomial<#ring>
%tensor = polynomial.to_tensor %poly : !polynomial.polynomial<#ring> -> tensor<1024xi32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputAn element of a polynomial ring.

Results:

ResultDescription
outputranked tensor of any type values

7.15 - Random

‘random’ Dialect

The random dialect contains operations used to generate random numbers.

Random types

DistributionType

A random distribution type

Syntax:

!random.distribution<
  ::mlir::heir::random::Distribution   # distribution_type
>

A generic type, representing a specific random distribution type of either uniform or gaussian as an attribute ($distribution_type).

Parameters:

ParameterC++ typeDescription
distribution_type::mlir::heir::random::Distribution

PRNGType

A pseudorandom number generator type

Syntax: !random.prng

A type that provides pseudorandom number generator.

Random ops

random.discrete_gaussian_distribution (heir::random::DiscreteGaussianDistributionOp)

Initializes the Discrete Gaussian Distribution

Syntax:

operation ::= `random.discrete_gaussian_distribution` operands attr-dict `:` functional-type(operands, results)

Initializes the Discrete Gaussian Distribution. The distribution is initialized with a mean and a standard deviation and pseudorandom generator that provides the source of the randomness.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
mean::mlir::IntegerAttrAn Attribute containing a integer value
stddev::mlir::IntegerAttrAn Attribute containing a integer value whose value is non-negative

Operands:

OperandDescription
inputA pseudorandom number generator type

Results:

ResultDescription
outputA random distribution type

random.discrete_uniform_distribution (heir::random::DiscreteUniformDistributionOp)

Initializes the Discrete Uniform Distribution

Syntax:

operation ::= `random.discrete_uniform_distribution` $input `{` `range` `=` `[` $min `,` $max `]` `}` attr-dict `:` `(` qualified(type($input)) `)` `->` type($output)

Initializes the Discrete Uniform Distribution. The distribution is initialized with a minimum and a maximum value and pseudo random generator that provides the source of the randomness. The distribution is inclusive of the minimum and exclusive of the maximum.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
min::mlir::IntegerAttrAn Attribute containing a integer value
max::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
inputA pseudorandom number generator type

Results:

ResultDescription
outputA random distribution type

random.init_prng (heir::random::InitOp)

Initializes the pseudorandom number generator with a seed.

Syntax:

operation ::= `random.init_prng` operands attr-dict `:` functional-type(operands, results)

Initializes the PRNG with a seed. The seed is dynamically provided due to protocols that agree on shared randomness. The PRNG is used to initialized the random distributions such as the discrete gaussian distribution and the discrete uniform distribution. This initialization also takes as input a number of bits that are generated for each number value sampled (num_bits). For instance, a num_bits of 32 will mean that distributions will generate a 32-bit integer value. We expect that the seed initialization is done statically and globally once per thread for all distributions; however, if multiple threads are generating randomness, then seed initialization should be done per thread; otherwise there is no guarantee of consistent behavior. Thread safety is so far not considered.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
num_bits::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
seedindex

Results:

ResultDescription
outputA pseudorandom number generator type

random.sample (heir::random::SampleOp)

Samples from a distribution

Syntax:

operation ::= `random.sample` operands attr-dict `:` functional-type(operands, results)

Samples from the distribution to obtain a random value or tensor of values.

Operands:

OperandDescription
inputA random distribution type

Results:

ResultDescription
outputany type

Random additional definitions

Distribution

An enum attribute representing a random distribution

Cases:

SymbolValueString
uniform0uniform
gaussian1gaussian

7.16 - RNS

‘rns’ Dialect

The rns dialect represents types and ops related to residue number system (RNS) representations of ring-like types, such as integers or polynomials decomposed from high-bit width to lower-bit-width prime moduli. Sometimes RNS is referred to as CRT, for “Chinese Remainder Theorem.”

This dialect is intended to be as generic as possible in terms of its interaction with standard MLIR. However, because of upstream MLIR constraints, we do not have the ability to override, say, arith.addi to operate on an rns type. So such situations require dedicated ops, canonicalization patterns, etc.

RNS types

RNSType

A residue number system representation

Syntax:

!rns.rns<
  ::llvm::ArrayRef<mlir::Type>   # basisTypes
>

Parameters:

ParameterC++ typeDescription
basisTypes::llvm::ArrayRef<mlir::Type>

RNS ops

rns.extract_slice (heir::rns::ExtractSliceOp)

Extracts a slice of RNS limbs

Syntax:

operation ::= `rns.extract_slice` $input attr-dict `:` type($input) `->` type($output)

Given an RNS-typed value with $k$ basis types (limbs), extract the slice of RNS components starting at start and having size size.

The result type is an RNS type containing the subset of basis types corresponding to the extracted slice. This is useful for operations like truncating or partitioning a modulus chain.

Traits: AlwaysSpeculatableImplTrait, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
start::mlir::IntegerAttrindex attribute
size::mlir::IntegerAttrindex attribute

Operands:

OperandDescription
inputrns-like

Results:

ResultDescription
outputrns-like

RNS additional definitions

TypeInterface definitions

RNSBasisTypeInterface (RNSBasisTypeInterface)

This interface is required for a type to be used as a parameter to an rns type.

Methods:

isCompatibleWith

bool isCompatibleWith(::mlir::Type otherRnsBasisType);

Returns true if this type is compatible with another type in the same RNS basis. In particular, the set of types used for a single RNS basis are never equal as types, but instead have some common attribute that must be checked here. For example, an RNS type where the basis types are polynomials would return true if the two types are both polynomial types, even if they have different coefficient moduli.

Another example is using mod arith types as the basis types, where by the nature of chinese reminder theorem, it is required that the modulus of them must be mutually coprime.

isCompatibleWith must be commutative, in the sense that type1.isCompatibleWith(type2) if and only if type2.isCompatibleWith(type1).

NOTE: This method must be implemented by the user.

7.17 - Secret

‘secret’ Dialect

Secret is a dialect for computations that operate on encrypted data.

Secret is intended to serve as a scheme-agnostic front-end for the HEIR ecosystem of dialects. It is supposed to be fully interoperable with the rest of MLIR via secret.generic, while lower-level HEIR dialects would have custom types for arithmetic on secret integers of various bit widths.

Secret attributes

KernelAttr

An annotation describing an implementation kernel for a given op.

Syntax:

#secret.kernel<
  ::mlir::heir::KernelName,   # name
  bool   # force
>

This attribute is used for two purposes:

  1. To allow the input IR to annotate fixed kernels on ops that the rest of the compiler must respect.
  2. To allow the layout optimization pipeline to materialize its kernel selection decisions to the IR.

The name field corresponds to an internally-defined kernel name, and if force is set to true, then the kernel may not be overridden by HEIR’s internal passes.

Parameters:

ParameterC++ typeDescription
name::mlir::heir::KernelName
forcebool

Secret types

SecretType

A secret value

Syntax:

!secret.secret<
  Type   # valueType
>

A generic wrapper around another MLIR type, representing an encrypted value but not specifying the manner of encryption. This is useful in HEIR because the compiler may choose various details of the FHE scheme based on the properties of the input program, the backend target hardware, and cost models of the various passes.

Parameters:

ParameterC++ typeDescription
valueTypeType

Secret ops

secret.cast (heir::secret::CastOp)

A placeholder cast from one secret type to another

Syntax:

operation ::= `secret.cast` $input attr-dict `:` qualified(type($input)) `to` qualified(type($output))

A cast operation represents a type cast from one secret type to another, that is used to enable the intermixing of various equivalent secret types before a lower-level FHE scheme has been chosen.

For example, secret.cast can be used to convert a secret<i8> to a secret<tensor<8xi1>> as a compatibility layer between boolean and non-boolean parts of a program. The pass that later lowers the IR to specific FHE schemes would need to replace these casts with appropriate scheme-specific operations, and it is left to those later passes to determine which casts are considered valid.

Example:

%result = secret.cast %0 : !secret.secret<i8> to !secret.secret<tensor<8xi1>>
%result2 = secret.cast %0 : !secret.secret<i8> to !secret.secret<tensor<2xi4>>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputA secret value

Results:

ResultDescription
outputA secret value

secret.conceal (heir::secret::ConcealOp)

Convert a non-secret value into a secret

Syntax:

operation ::= `secret.conceal` $cleartext attr-dict `:` qualified(type($cleartext)) `->` qualified(type($output))

Convert a value to a secret containing the same value.

This op represents a scheme-agnostic encryption operation, as well as a “trivial encryption” operation which is needed for some FHE schemes. This op is also useful for type materialization in the dialect conversion framework.

Examples:

%Y = secret.conceal %value : i32 -> !secret.secret<i32>

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
cleartextany type

Results:

ResultDescription
outputA secret value

secret.generic (heir::secret::GenericOp)

Lift a plaintext computation to operate on secrets.

secret.generic lifts a plaintext computation to operate on one or more secrets. The lifted computation is represented as a region containing a single block terminated by secret.yield. The arguments of the secret.generic may include one or more !secret.secret types. The arguments of the block in the op’s body correspond to the underlying plaintext types of the secrets.

secret.generic is not isolated from above, so you may directly reference values in the enclosing scope. This is required to support using secret.generic inside of ops with AffineScope, while having the body of the generic use the induction variables defined by the affine scope.

Basic examples:

Add two secret integers together

%Z = secret.generic(%X, %Y : !secret.secret<i32>, !secret.secret<i32>) {
  ^bb0(%x: i32, %y: i32):
    %z = arith.addi %x, %y: i32
    secret.yield %z : i32
  } -> (!secret.secret<i32>)

Add a secret value with a plaintext value. I.e., not all arguments to the op need be secret.

%Z = secret.generic(%X, %Y : i32, !secret.secret<i32>) {
  ^bb0(%x: i32, %y: i32):
    %z = arith.addi %x, %y: i32
    secret.yield %z : i32
  } -> (!secret.secret<i32>)

The same as above, but the plaintext op is not passed through the basic block.

%y = arith.constant 7: i32
%Z = secret.generic(%X : !secret.secret<i32>) {
  ^bb0(%x: i32):
    %z = arith.addi %x, %y: i32
    secret.yield %z : i32
  } -> (!secret.secret<i32>)

Traits: SingleBlockImplicitTerminator<YieldOp>, SingleBlock

Interfaces: OpAsmOpInterface, OperandAndResultAttrInterface, RegionBranchOpInterface

Operands:

OperandDescription
inputsvariadic of any type

Results:

ResultDescription
resultsvariadic of any type

secret.reveal (heir::secret::RevealOp)

Convert a secret value into a non-secret

Syntax:

operation ::= `secret.reveal` $input attr-dict `:` qualified(type($input)) `->` qualified(type($cleartext))

Convert a secret into a non-secret containing the same value.

This op represents a scheme-agnostic decryption operation. This op is also useful for target materialization in the dialect conversion framework.

Examples:

%Y = secret.reveal %secret_value : !secret.secret<i32> -> i32

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
inputA secret value

Results:

ResultDescription
cleartextany type

secret.separator (heir::secret::SeparatorOp)

Convert a non-secret value into a secret

Syntax:

operation ::= `secret.separator` attr-dict ($inputs^ `:` type($inputs))?

This operation is used as a separation boundary between logical subunits of the module. This is used in conjunction with --secret-distribute-generic=distribute-through=secret.separator to break a generic around these separators and allow for optimization passes to analyze and optimize the sub-units locally.

In order to allow bufferization of modules with this operation, we must register a (bogus) memory effect that also prevents this operation from being trivially dead during operation folding.

This operation also accepts operands, which act as boundaries between the logical units. This enforces separation of memref and affine optimizations between the subunits, preventing optimizations from removing the operand and combining the two separated regions. The operand can be thought of as an return value of the logical subunit.

Interfaces: MemoryEffectOpInterface (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{MemoryEffects::Write on ::mlir::SideEffects::DefaultResource}

Operands:

OperandDescription
inputsvariadic of any type

secret.yield (heir::secret::YieldOp)

Secret yield operation

secret.yield is a special terminator operation for blocks inside regions in secret generic ops. It returns the cleartext value of the corresponding private computation to the immediately enclosing secret generic op.

Traits: AlwaysSpeculatableImplTrait, HasParent<GenericOp>, ReturnLike, Terminator

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface), RegionBranchTerminatorOpInterface

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
valuesvariadic of any type

7.18 - TensorExt

’tensor_ext’ Dialect

The tensor_ext dialect contains operations on plaintext tensors that correspond to the computation model of certain FHE schemes, but are unlikely to be upstreamed to MLIR due to their specificity to FHE.

TensorExt attributes

LayoutAttr

The description of the layout of a data-semantic tensor.

Syntax:

#tensor_ext.layout<
  mlir::StringAttr   # layout
>

This attribute describes how a data-semantic tensor is laid out among a tensor of ciphertexts. The layout is described by an integer relation $(d, s)$, where $d$ is a multiset of data-semantic tensor indices and $s$ is a multiset of slot indices (or coefficient indices). The slot indices are defined by two indices: the ciphertext index and the slot index in that order. The elements of the relation are defined by a set of quasi-affine constraints.

I.e., a point $((2, 3), (7, 0))$ in the relation says that the data entry at index $(2, 3)$ is placed in slot 0 of ciphertext 7. This could be defined as part of the relation by a constraint like row + col + 2 - ct + slot = 0.

The attribute stores a string representation of the integer relation, which follows the ISL syntax for isl_basic_map. For example:

#vec_layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : (i0 - slot) mod 1024 = 7 and i0 >= 0 and 0 >= i0 and slot >= 0 and 1023 >= slot and ct = 0 }">

#mat_layout = #tensor_ext.layout<"{ [row, col] -> [ct, slot] : (slot - row) mod 512 = 0 and (ct + slot - col) mod 512 = 0 and row >= 0 and col >= 0 and ct >= 0 and slot >= 0 and 1023 >= slot and 511 >= ct and 511 >= row and 511 >= col }">

// Example with local (existential) variables.
#layout = #tensor_ext.layout<"{[d0] -> [ct, slot] : exists d3, d4 : -ct + d3 = 0 and d0 - d4 * 1024 = 0 and -d0 + 31 >= 0 and d0 >= 0 and ct >= 0 and slot >= 0 and -slot + 1023 >= 0 and -d0 + d3 * 1024 + 1023 >= 0 and d0 - d3 * 1024 >= 0 and -d0 + d4 * 1024 + 1023 >= 0 and d0 - d4 * 1024 >= 0 }">

Parameters:

ParameterC++ typeDescription
layoutmlir::StringAttr

OriginalTypeAttr

The original type of a secret tensor whose layout has been converted to ciphertext semantics.

Syntax:

#tensor_ext.original_type<
  ::mlir::Type,   # originalType
  ::mlir::Attribute   # layout
>

This attribute is used to retain the original type of a secret tensor after its conversion to ciphertext semantics, i.e. after applying any padding or alignment to fill ciphertext data types. For example, if a !secret.secret<tensor<32xi8>> is laid out in a ciphertext with 1024 slots, the new type would be !secret.secret<tensor<1024xi8>> with attribute tensor_ext.original_type<!secret.secret<tensor<32xi8>>.

Parameters:

ParameterC++ typeDescription
originalType::mlir::Type
layout::mlir::Attribute

TensorExt ops

tensor_ext.assign_layout (heir::tensor_ext::AssignLayoutOp)

Assign a layout to a plaintext tensor or scalar.

Syntax:

operation ::= `tensor_ext.assign_layout` operands attr-dict `:` type($output)

This op allows the ingestion of a plaintext value into the layout system. For example, ops like linalg.reduce, require a tensor input to represent initial values. These will generally be created by an arith.constant or tensor.empty op, which does not have secret results. Lowerings will convert this to a packed plaintext, so that the subsequent ops can be lowered as ciphertext-plaintext ops.

This op is inserted by layout selection passes.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
layout::mlir::AttributeThe description of the layout of a data-semantic tensor.

Operands:

OperandDescription
valueany type

Results:

ResultDescription
outputany type

tensor_ext.convert_layout (heir::tensor_ext::ConvertLayoutOp)

Convert from one layout to another.

Syntax:

operation ::= `tensor_ext.convert_layout` operands attr-dict `:` type($output)

This op represents the conversion of a value from one packed layout to another. This is implemented via a “shift network” of ciphertext rotations, plaintext masks (ciphertext-plaintext multiplications), and additions.

This op is inserted by layout selection passes.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
from_layout::mlir::AttributeThe description of the layout of a data-semantic tensor.
to_layout::mlir::AttributeThe description of the layout of a data-semantic tensor.

Operands:

OperandDescription
valueany type

Results:

ResultDescription
outputany type

tensor_ext.remap (heir::tensor_ext::RemapOp)

Reorganize the entries of a tensor by a static mapping.

Syntax:

operation ::= `tensor_ext.remap` operands attr-dict `:` type($input)

This op represents a remapping of entries of a tensor.

This op is primarily inserted as a lowered form of convert_layout op, to represent a ciphertext slot-repacking operation. However, it can more generally express any partial mapping from source tensor indices to target indices within a tensor. Unmapped entries from the input tensor are unmodified.

This operation differs from a tensor.gather/scatter operation in that it can replicate values from the source tensor or omit values in the destination tensor. It differs from a “lane shuffle” in that the mapping need not be a permutation. It differs from a “swizzle” in that it cannot change the dimension of the result tensor.

In the slot form of a ciphertext, this op is lowered to a “shift network” of ciphertext-plaintext mask, rotate, and sum operations by the implement-shift-network pass.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
permutation::mlir::Attribute64-bit integer elements attribute or The description of the layout of a data-semantic tensor.

Operands:

OperandDescription
inputranked tensor of any type values

Results:

ResultDescription
outputranked tensor of any type values

tensor_ext.rotate_and_reduce (heir::tensor_ext::RotateAndReduceOp)

Performs a reduction of a periodically rotated tensor.

Syntax:

operation ::= `tensor_ext.rotate_and_reduce` operands attr-dict `:` functional-type(operands, results)

This op reduces products of a plaintext with a periodically rotated tensor.

In almost full generality, the reduction performed is

[ \sum_{i \in [0, n]} p(P, Ti) \cdot rotate(v, Ti) ]

where $f$ is a function, $p(P, Ti)$ is a function of a plaintext $P$ and $rotate(v, Ti)$ is a rotation of the ciphertext $v$ with period $T$. The operation takes as input the ciphertext vector $v$, the period $T$, the number of reductions $n$, and a tensor of plaintext values [p(P, 0), p(P, T), ..., p(P, T*(n-1))].

This can be used to implement a matrix vector product that uses a Halevi-Shoup diagonalization of the plaintext matrix. In this case, the reduction is

[ \sum_{i \in [0, n]} P(i) \cdot rotate(v, i) ]

where $P(i)$ is the $i$th diagonal of the plaintext matrix and the period $T$ is $1$.

An accumulation of the ciphertext slots is also handled via this operation by omitting the plaintext $p(P, T*i)$ argument and using a period of 1 with n = |v| so that the reduction is simply a sum of all rotation of the ciphertext.

If reduceOp is set to an MLIR operation name (e.g., arith.mulf), then the reduction operation is modified to use that operation instead of a sum. The chosen op must be one of arith.muli, arith.mulf, arith.addi, or arith.addf.

Efficient lowerings of this operation can use the Baby-Step / Giant-Step approach from Faster Homomorphic Linear Transformations in HElib to reduce the number of ciphertext rotations.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
period::mlir::IntegerAttrindex attribute
steps::mlir::IntegerAttrindex attribute
reduceOp::mlir::StringAttrAn Attribute containing a string

Operands:

OperandDescription
tensorranked tensor of any type values
plaintextsranked tensor of any type values

Results:

ResultDescription
outputranked tensor of any type values

tensor_ext.rotate (heir::tensor_ext::RotateOp)

Rotate a tensor some number of indices left.

Syntax:

operation ::= `tensor_ext.rotate` operands attr-dict `:` qualified(type($tensor)) `,` type($shift)

This op represents a left-rotation of a tensor by given number of indices. Negative shift values are interpreted as right-rotations.

This corresponds to the rotate operation in arithmetic FHE schemes like BGV. This op currently only supports 1D rotations of the last axis of a tensor. A tensor<4x64xi32> is interpreted as 4 ciphertexts each with 64 slots, and a rotation on a value of this type rotates each ciphertext by the given amount.

// In the future, the op will be adjusted to support rotations of general // multi-dimensional tensors with a vector of rotation indices for each // dimension. The lowering will implement the correct operations to rotate // the tensor along the indices given its packing.

Examples:

%0 = ... : tensor<16xi32>
%c7 = arith.constant 7 : i32
%1 = tensor_ext.rotate %0, %c7 : tensor<16xi32>, i32

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
tensorranked tensor of any type values
shiftsignless-integer-like

Results:

ResultDescription
outputranked tensor of any type values

tensor_ext.unpack (heir::tensor_ext::UnpackOp)

Unpack data from a ciphertext-semantic tensor.

Syntax:

operation ::= `tensor_ext.unpack` operands attr-dict `:` functional-type(operands, results)

This op extracts the underlying cleartext data from a ciphertext-semantic tensor.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
layout::mlir::AttributeThe description of the layout of a data-semantic tensor.

Operands:

OperandDescription
valueany type

Results:

ResultDescription
outputany type

7.19 - TfheRust

’tfhe_rust’ Dialect

The thfe_rust dialect is an exit dialect for generating rust code against the tfhe-rs library API, using the shortint parameters and encoding scheme.

See https://github.com/zama-ai/tfhe-rs

TfheRust types

EncryptedBoolType

An encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs. Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp.

Syntax: !tfhe_rust.bool

EncryptedInt2Type

An encrypted signed integer corresponding to tfhe-rs’s FHEInt2 type

Syntax: !tfhe_rust.ei2

EncryptedInt4Type

An encrypted signed integer corresponding to tfhe-rs’s FHEInt4 type

Syntax: !tfhe_rust.ei4

EncryptedInt8Type

An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type

Syntax: !tfhe_rust.ei8

EncryptedInt16Type

An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type

Syntax: !tfhe_rust.ei16

EncryptedInt32Type

An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type

Syntax: !tfhe_rust.ei32

EncryptedInt64Type

An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type

Syntax: !tfhe_rust.ei64

EncryptedInt128Type

An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type

Syntax: !tfhe_rust.ei128

EncryptedInt256Type

An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

Syntax: !tfhe_rust.ei256

EncryptedUInt2Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type

Syntax: !tfhe_rust.eui2

EncryptedUInt3Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type

Syntax: !tfhe_rust.eui3

EncryptedUInt4Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type

Syntax: !tfhe_rust.eui4

EncryptedUInt8Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type

Syntax: !tfhe_rust.eui8

EncryptedUInt10Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type

Syntax: !tfhe_rust.eui10

EncryptedUInt12Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type

Syntax: !tfhe_rust.eui12

EncryptedUInt14Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type

Syntax: !tfhe_rust.eui14

EncryptedUInt16Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type

Syntax: !tfhe_rust.eui16

EncryptedUInt32Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type

Syntax: !tfhe_rust.eui32

EncryptedUInt64Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type

Syntax: !tfhe_rust.eui64

EncryptedUInt128Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type

Syntax: !tfhe_rust.eui128

EncryptedUInt256Type

An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type

Syntax: !tfhe_rust.eui256

LookupTableType

A univariate lookup table used for programmable bootstrapping.

Syntax: !tfhe_rust.lookup_table

ServerKeyType

The short int server key required to perform homomorphic operations.

Syntax: !tfhe_rust.server_key

TfheRust ops

tfhe_rust.add (heir::tfhe_rust::AddOp)

Arithmetic add of two tfhe ciphertexts.

Syntax:

operation ::= `tfhe_rust.add` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhsAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type
rhsInteger type with arbitrary precision up to a fixed limit or An encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

Results:

ResultDescription
outputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

tfhe_rust.apply_lookup_table (heir::tfhe_rust::ApplyLookupTableOp)

Syntax:

operation ::= `tfhe_rust.apply_lookup_table` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
inputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type
lookupTableA univariate lookup table used for programmable bootstrapping.

Results:

ResultDescription
outputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

tfhe_rust.bitand (heir::tfhe_rust::BitAndOp)

Logical AND of two tfhe ciphertexts.

Syntax:

operation ::= `tfhe_rust.bitand` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhstfhe-ciphertext-like
rhstfhe-ciphertext-like

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.bitor (heir::tfhe_rust::BitOrOp)

Logical OR of two tfhe ciphertexts.

Syntax:

operation ::= `tfhe_rust.bitor` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhstfhe-ciphertext-like
rhstfhe-ciphertext-like

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.bitxor (heir::tfhe_rust::BitXorOp)

Logical XOR of two tfhe ciphertexts.

Syntax:

operation ::= `tfhe_rust.bitxor` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhstfhe-ciphertext-like
rhstfhe-ciphertext-like

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.cast (heir::tfhe_rust::CastOp)

Syntax:

operation ::= `tfhe_rust.cast` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
ciphertextAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

Results:

ResultDescription
outputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

tfhe_rust.cmp (heir::tfhe_rust::CmpOp)

_High level operation to check the relation of two ciphertexts.

  • equal (mnemonic: “eq”; integer value: 0)
  • not equal (mnemonic: “ne”; integer value: 1)
  • signed less than (mnemonic: “slt”; integer value: 2)
  • signed less than or equal (mnemonic: “sle”; integer value: 3)
  • signed greater than (mnemonic: “sgt”; integer value: 4)
  • signed greater than or equal (mnemonic: “sge”; integer value: 5)
  • unsigned less than (mnemonic: “ult”; integer value: 6)
  • unsigned less than or equal (mnemonic: “ule”; integer value: 7)
  • unsigned greater than (mnemonic: “ugt”; integer value: 8)
  • unsigned greater than or equal (mnemonic: “uge”; integer value: 9)

Note: https://mlir.llvm.org/docs/Dialects/ArithOps/#arithcmpi-arithcmpiop_

Syntax:

operation ::= `tfhe_rust.cmp` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
predicate::mlir::arith::CmpIPredicateAttrallowed 64-bit signless integer cases: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhsAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type
rhsAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

Results:

ResultDescription
outputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp.

tfhe_rust.create_trivial (heir::tfhe_rust::CreateTrivialOp)

Syntax:

operation ::= `tfhe_rust.create_trivial` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
valueinteger

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.eq (heir::tfhe_rust::EqOp)

High level operation to check equality of two ciphertexts.

Syntax:

operation ::= `tfhe_rust.eq` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhstfhe-ciphertext-like
rhstfhe-ciphertext-like

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.generate_lookup_table (heir::tfhe_rust::GenerateLookupTableOp)

Syntax:

operation ::= `tfhe_rust.generate_lookup_table` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
truthTable::mlir::IntegerAttrAn Attribute containing a integer value

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.

Results:

ResultDescription
lookupTableA univariate lookup table used for programmable bootstrapping.

tfhe_rust.max (heir::tfhe_rust::MaxOp)

High level operation to return maximum of two ciphertexts.

Syntax:

operation ::= `tfhe_rust.max` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhstfhe-ciphertext-like
rhstfhe-ciphertext-like

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.min (heir::tfhe_rust::MinOp)

High level operation to return minimum of two ciphertexts.

Syntax:

operation ::= `tfhe_rust.min` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhstfhe-ciphertext-like
rhstfhe-ciphertext-like

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.mul (heir::tfhe_rust::MulOp)

Arithmetic mul of two tfhe ciphertexts.

Syntax:

operation ::= `tfhe_rust.mul` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhsAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type
rhsInteger type with arbitrary precision up to a fixed limit or An encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

Results:

ResultDescription
outputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

tfhe_rust.neq (heir::tfhe_rust::NeqOp)

High level operation to check inequality of two ciphertexts.

Syntax:

operation ::= `tfhe_rust.neq` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhstfhe-ciphertext-like
rhstfhe-ciphertext-like

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.scalar_left_shift (heir::tfhe_rust::ScalarLeftShiftOp)

Syntax:

operation ::= `tfhe_rust.scalar_left_shift` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
shiftAmount::mlir::IntegerAttrindex attribute

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
ciphertextAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

Results:

ResultDescription
outputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

tfhe_rust.scalar_right_shift (heir::tfhe_rust::ScalarRightShiftOp)

Syntax:

operation ::= `tfhe_rust.scalar_right_shift` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
shiftAmount::mlir::IntegerAttrindex attribute

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
ciphertextAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

Results:

ResultDescription
outputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

tfhe_rust.cmux (heir::tfhe_rust::SelectOp)

Multiplexer operations, the select ciphertext will return the trueCtxt if in contains a 1. In the other case, it will will return the falseCtxt.

Syntax:

operation ::= `tfhe_rust.cmux` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
selectAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp.
trueCtxttfhe-ciphertext-like
falseCtxttfhe-ciphertext-like

Results:

ResultDescription
outputtfhe-ciphertext-like

tfhe_rust.sub (heir::tfhe_rust::SubOp)

Arithmetic sub of two tfhe ciphertexts.

Syntax:

operation ::= `tfhe_rust.sub` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe short int server key required to perform homomorphic operations.
lhstfhe-ciphertext-like
rhsInteger type with arbitrary precision up to a fixed limit or An encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

Results:

ResultDescription
outputAn encrypted bool corresponding to tfhe-rs’s FHEBool, not in the Boolean TFHE-rs.
Note this is not an encryption of a boolean, but the outcome of operations as Eq or Cmp. or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint2 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint3 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint4 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint8 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint10 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint12 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint14 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint16 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint32 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint64 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint128 type or An encrypted unsigned integer corresponding to tfhe-rs’s FHEUint256 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt8 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt16 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt32 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt64 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt128 type or An encrypted signed integer corresponding to tfhe-rs’s FHEInt256 type

7.20 - TfheRustBool

’tfhe_rust_bool’ Dialect

The tfhe_rust_bool dialect is an exit dialect for generating rust code against the tfhe-rs library API, using the boolean parameter set.

See https://github.com/zama-ai/tfhe-rs

TfheRustBool attributes

TfheRustBoolGatesAttr

An Attribute containing an array of strings to store bool gates

Syntax:

#tfhe_rust_bool.tfhe_rust_bool_gates<
  ::llvm::ArrayRef<::mlir::heir::tfhe_rust_bool::TfheRustBoolGateEnumAttr>   # gates
>

This attributes stores a list of integer identifiers for Boolean gates.

Uses following mapping: AND_GATE = 0; NAND_GATE = 1; OR_GATE = 2; NOR_GATE = 3; XOR_GATE = 4; XNOR_GATE = 5; NOT_GATE = 6;

Parameters:

ParameterC++ typeDescription
gates::llvm::ArrayRef<::mlir::heir::tfhe_rust_bool::TfheRustBoolGateEnumAttr>

TfheRustBool types

EncryptedBoolType

An encrypted Boolean corresponding to tfhe-rs’s FHEBool type

Syntax: !tfhe_rust_bool.eb

PackedServerKeyType

The Belfort packed API boolean server key.

Syntax: !tfhe_rust_bool.server_key_enum

ServerKeyType

The boolean server key required to perform homomorphic operations.

Syntax: !tfhe_rust_bool.server_key

TfheRustBool ops

tfhe_rust_bool.create_trivial (heir::tfhe_rust_bool::CreateTrivialOp)

Syntax:

operation ::= `tfhe_rust_bool.create_trivial` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeytfhe rust bool server key
value1-bit signless integer

Results:

ResultDescription
outputAn encrypted Boolean corresponding to tfhe-rs’s FHEBool type

tfhe_rust_bool.and (heir::tfhe_rust_bool::AndOp)

Logical AND of two TFHE-rs Bool ciphertexts.

Syntax:

operation ::= `tfhe_rust_bool.and` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
lhseb-like
rhseb-like

Results:

ResultDescription
outputeb-like

tfhe_rust_bool.mux (heir::tfhe_rust_bool::MuxOp)

Syntax:

operation ::= `tfhe_rust_bool.mux` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
cndAn encrypted Boolean corresponding to tfhe-rs’s FHEBool type
lhsAn encrypted Boolean corresponding to tfhe-rs’s FHEBool type
rhsAn encrypted Boolean corresponding to tfhe-rs’s FHEBool type

Results:

ResultDescription
outputAn encrypted Boolean corresponding to tfhe-rs’s FHEBool type

tfhe_rust_bool.nand (heir::tfhe_rust_bool::NandOp)

Logical NAND of two TFHE-rs Bool ciphertexts.

Syntax:

operation ::= `tfhe_rust_bool.nand` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
lhseb-like
rhseb-like

Results:

ResultDescription
outputeb-like

tfhe_rust_bool.nor (heir::tfhe_rust_bool::NorOp)

Logical NOR of two TFHE-rs Bool ciphertexts.

Syntax:

operation ::= `tfhe_rust_bool.nor` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
lhseb-like
rhseb-like

Results:

ResultDescription
outputeb-like

tfhe_rust_bool.not (heir::tfhe_rust_bool::NotOp)

Syntax:

operation ::= `tfhe_rust_bool.not` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
inputeb-like

Results:

ResultDescription
outputeb-like

tfhe_rust_bool.or (heir::tfhe_rust_bool::OrOp)

Logical OR of two TFHE-rs Bool ciphertexts.

Syntax:

operation ::= `tfhe_rust_bool.or` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
lhseb-like
rhseb-like

Results:

ResultDescription
outputeb-like

tfhe_rust_bool.gates_packed (heir::tfhe_rust_bool::PackedOp)

Syntax:

operation ::= `tfhe_rust_bool.gates_packed` operands attr-dict `:` functional-type(operands, results)

Operation to where different Boolean gates are executed pairwise between elements of two ciphertext arrays.

For example,

%0 = tfhe_rust_bool.packed_gates %a, %b {gates = #tfhe_rust_bool.tfhe_rust_bool_gates<0 : i32, 4 : i32>} :
    (!tfhe_rust_bool.server_key,
     tensor<2x!tfhe_rust_bool.eb>,
     tensor<2x!tfhe_rust_bool.eb>) -> tensor<2x!tfhe_rust_bool.eb>

applies an “and” gate to the first elements of %a and %b and an xor gate to the second elements.

Mapping is defined in the BooleanGates.td file.

Traits: AlwaysSpeculatableImplTrait

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Attributes:

AttributeMLIR TypeDescription
gates::mlir::heir::tfhe_rust_bool::TfheRustBoolGatesAttrAn Attribute containing an array of strings to store bool gates

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
lhseb-like
rhseb-like

Results:

ResultDescription
outputeb-like

tfhe_rust_bool.xnor (heir::tfhe_rust_bool::XnorOp)

Logical XNOR of two TFHE-rs Bool ciphertexts.

Syntax:

operation ::= `tfhe_rust_bool.xnor` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
lhseb-like
rhseb-like

Results:

ResultDescription
outputeb-like

tfhe_rust_bool.xor (heir::tfhe_rust_bool::XorOp)

Logical XOR of two TFHE-rs Bool ciphertexts.

Syntax:

operation ::= `tfhe_rust_bool.xor` operands attr-dict `:` functional-type(operands, results)

Traits: AlwaysSpeculatableImplTrait, Commutative, Elementwise, Scalarizable, Tensorizable, Vectorizable

Interfaces: ConditionallySpeculatable, InferTypeOpInterface, NoMemoryEffect (MemoryEffectOpInterface)

Effects: MemoryEffects::Effect{}

Operands:

OperandDescription
serverKeyThe boolean server key required to perform homomorphic operations. or The Belfort packed API boolean server key.
lhseb-like
rhseb-like

Results:

ResultDescription
outputeb-like

TfheRustBool additional definitions

TfheRustBoolGateEnum

An enum attribute representing a TFHE-rs boolean gate using u8 int

Cases:

SymbolValueString
AND0AND
NAND1NAND
OR2OR
NOR3NOR
XOR4XOR
XNOR5XNOR
NOT6NOT

8 - Passes

-add-client-interface

Add client interfaces to secret functions

This pass adds encrypt and decrypt functions for each compiled function in the IR. These functions maintain the same interface as the original function, while the compiled function may lose some of this information by the lowerings to ciphertext types (e.g., a scalar ciphertext, when lowered through RLWE schemes, must be encoded as a tensor).

This pass occurs at the secret level, which is necessary because some backends like the plaintext backend don’t actually encrypt, but still require the ciphertext layout/packing logic to convert cleartexts to plaintexts.

Example

Command: heir-opt --add-client-interface=ciphertext-size=1024 tests/Transforms/add_client_interface/doctest.mlir

Input:

!ct_ty = !secret.secret<tensor<1x1024xi16>>
#layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : (slot - i0) mod 32 = 0 and ct = 0 and 1023 >= slot >= 0 and 31 >= i0 >= 0 }">
#original_type = #tensor_ext.original_type<originalType = tensor<32xi16>, layout = #layout>

func.func @simple_add(
    %arg0: !ct_ty {tensor_ext.original_type = #original_type},
    %arg1: !ct_ty {tensor_ext.original_type = #original_type}
) -> (!ct_ty {tensor_ext.original_type = #original_type}) {
  %0 = secret.generic(%arg0: !ct_ty, %arg1: !ct_ty) {
  ^body(%pt_arg0: tensor<1x1024xi16>, %pt_arg1: tensor<1x1024xi16>):
    %1 = arith.addi %pt_arg0, %pt_arg1 : tensor<1x1024xi16>
    secret.yield %1 : tensor<1x1024xi16>
  } -> !ct_ty
  return %0 : !ct_ty
}

Output:

#layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : (slot - i0) mod 32 = 0 and ct = 0 and 1023 >= slot >= 0 and 31 >= i0 >= 0 }">
#original_type = #tensor_ext.original_type<originalType = tensor<32xi16>, layout = #layout>
module {
  func.func @simple_add(%arg0: !secret.secret<tensor<1x1024xi16>> {tensor_ext.original_type = #original_type}, %arg1: !secret.secret<tensor<1x1024xi16>> {tensor_ext.original_type = #original_type}) -> (!secret.secret<tensor<1x1024xi16>> {tensor_ext.original_type = #original_type}) {
    %0 = secret.generic(%arg0: !secret.secret<tensor<1x1024xi16>>, %arg1: !secret.secret<tensor<1x1024xi16>>) {
    ^body(%input0: tensor<1x1024xi16>, %input1: tensor<1x1024xi16>):
      %1 = arith.addi %input0, %input1 : tensor<1x1024xi16>
      secret.yield %1 : tensor<1x1024xi16>
    } -> !secret.secret<tensor<1x1024xi16>>
    return %0 : !secret.secret<tensor<1x1024xi16>>
  }
  func.func @simple_add__encrypt__arg0(%arg0: tensor<32xi16>) -> !secret.secret<tensor<1x1024xi16>> attributes {client.enc_func = {func_name = "simple_add", index = 0 : i64}} {
    %cst = arith.constant dense<0> : tensor<1x1024xi16>
    %c0 = arith.constant 0 : index
    %c1023 = arith.constant 1023 : index
    %c1 = arith.constant 1 : index
    %0 = arith.addi %c1023, %c1 : index
    %c1_0 = arith.constant 1 : index
    %1 = scf.for %arg1 = %c0 to %0 step %c1_0 iter_args(%arg2 = %cst) -> (tensor<1x1024xi16>) {
      %c32 = arith.constant 32 : index
      %3 = arith.remsi %arg1, %c32 : index
      %c0_1 = arith.constant 0 : index
      %extracted = tensor.extract %arg0[%3] : tensor<32xi16>
      %inserted = tensor.insert %extracted into %arg2[%c0_1, %arg1] : tensor<1x1024xi16>
      scf.yield %inserted : tensor<1x1024xi16>
    }
    %2 = secret.conceal %1 : tensor<1x1024xi16> -> !secret.secret<tensor<1x1024xi16>>
    return %2 : !secret.secret<tensor<1x1024xi16>>
  }
  func.func @simple_add__encrypt__arg1(%arg0: tensor<32xi16>) -> !secret.secret<tensor<1x1024xi16>> attributes {client.enc_func = {func_name = "simple_add", index = 1 : i64}} {
    %cst = arith.constant dense<0> : tensor<1x1024xi16>
    %c0 = arith.constant 0 : index
    %c1023 = arith.constant 1023 : index
    %c1 = arith.constant 1 : index
    %0 = arith.addi %c1023, %c1 : index
    %c1_0 = arith.constant 1 : index
    %1 = scf.for %arg1 = %c0 to %0 step %c1_0 iter_args(%arg2 = %cst) -> (tensor<1x1024xi16>) {
      %c32 = arith.constant 32 : index
      %3 = arith.remsi %arg1, %c32 : index
      %c0_1 = arith.constant 0 : index
      %extracted = tensor.extract %arg0[%3] : tensor<32xi16>
      %inserted = tensor.insert %extracted into %arg2[%c0_1, %arg1] : tensor<1x1024xi16>
      scf.yield %inserted : tensor<1x1024xi16>
    }
    %2 = secret.conceal %1 : tensor<1x1024xi16> -> !secret.secret<tensor<1x1024xi16>>
    return %2 : !secret.secret<tensor<1x1024xi16>>
  }
  func.func @simple_add__decrypt__result0(%arg0: !secret.secret<tensor<1x1024xi16>>) -> tensor<32xi16> attributes {client.dec_func = {func_name = "simple_add", index = 0 : i64}} {
    %0 = secret.reveal %arg0 : !secret.secret<tensor<1x1024xi16>> -> tensor<1x1024xi16>
    %cst = arith.constant dense<0> : tensor<32xi16>
    %c0 = arith.constant 0 : index
    %c1023 = arith.constant 1023 : index
    %c1 = arith.constant 1 : index
    %1 = arith.addi %c1023, %c1 : index
    %c1_0 = arith.constant 1 : index
    %2 = scf.for %arg1 = %c0 to %1 step %c1_0 iter_args(%arg2 = %cst) -> (tensor<32xi16>) {
      %c32 = arith.constant 32 : index
      %3 = arith.remsi %arg1, %c32 : index
      %c0_1 = arith.constant 0 : index
      %extracted = tensor.extract %0[%c0_1, %arg1] : tensor<1x1024xi16>
      %inserted = tensor.insert %extracted into %arg2[%3] : tensor<32xi16>
      scf.yield %inserted : tensor<32xi16>
    }
    return %2 : tensor<32xi16>
  }
}

Options

-ciphertext-size          : Power of two length of the ciphertexts the data is packed in.
-enable-layout-assignment : If false, skips the emission of layout assignment operations, essentially assuming that the input was already using correctly (ciphertext-)sized tensors.

-annotate-mgmt

Annotate MgmtAttr for secret SSA values in the IR

This pass runs the secretness/level/dimension analysis and annotates the IR with the results, saving it into each op’s attribute dictionary as mgmt.mgmt :

Options

-base-level : Level to start counting from (used by B/FV)

-annotate-module

Annotate ModuleOp with Scheme And/Or Backend

This pass annotates the module with a scheme and/or backend.

This pass should be called before all lowering to enable lowering to the desired scheme and backend.

Available scheme:

  • bgv
  • ckks
  • bfv
  • cggi

Available backend:

  • openfhe
  • lattigo

Example

Command: heir-opt --annotate-module="backend=openfhe scheme=ckks" tests/Transforms/annotate_module/pass.mlir

Input:

module {

}

Output:

module attributes {backend.openfhe, scheme.ckks} {
}

Options

-scheme  : The scheme to annotate the module with.
-backend : The backend to annotate the module with.

-annotate-secretness

Annotate secret SSA values in the IR

Debugging helper that runs the secretness analysis and annotates the IR with the results, extending the {secret.secret} annotation to all operation results that are secret.

In addition to annotating operation results, the pass also annotates arguments and return types in func.func operations, as well as any terminators (e.g. return)

In verbose mode, all results are annotated, including public ones with {secret.public}, and values for which the secretness analysis is missing are annotated with {secret.missing}, while values where the secretness analysis is inconclusive are annotated with {secret.unknown}.

Example

Command: heir-opt --annotate-secretness='verbose=true' tests/Transforms/annotate_secretness/doctest.mlir

Input:

func.func @mixed_secretness(%secret: !secret.secret<i32>, %public: i32) -> !secret.secret<i32> {
  %0 = secret.generic(%secret: !secret.secret<i32>, %public: i32) {
  ^body(%secret_val: i32, %public_val: i32):
    %1 = arith.addi %public_val, %public_val : i32          // public + public = public
    %2 = arith.muli %secret_val, %secret_val : i32          // secret * secret = secret
    %3 = arith.addi %secret_val, %public_val : i32          // secret + public = secret
    %4 = arith.addi %2, %3 : i32                           // secret + secret = secret
    secret.yield %4 : i32
  } -> !secret.secret<i32>
  return %0 : !secret.secret<i32>
}

Output:

module {
  func.func @mixed_secretness(%arg0: !secret.secret<i32> {secret.secret}, %arg1: i32 {secret.public}) -> (!secret.secret<i32> {secret.secret}) {
    %0 = secret.generic(%arg0: !secret.secret<i32>, %arg1: i32) attrs = {secret.secret} {
    ^body(%input0: i32, %input1: i32):
      %1 = arith.addi %input1, %input1 {secret.public} : i32
      %2 = arith.muli %input0, %input0 {secret.secret} : i32
      %3 = arith.addi %input0, %input1 {secret.secret} : i32
      %4 = arith.addi %2, %3 {secret.secret} : i32
      secret.yield %4 {secret.secret} : i32
    } -> !secret.secret<i32>
    return {secret.secret} %0 : !secret.secret<i32>
  }
}

Options

-verbose : If true, annotate secretness state all values, including public ones, and values with missing or inconclusive analysis.

-apply-folders

Apply all folding patterns from canonicalize

This pass applies all registered folding patterns greedily to the input IR. This is useful when running a full canonicalize is too slow, but applying folders before canonicalize is sufficient to simplify the IR for later passes, or even sufficient to then subsequently run a full canonicalize pass.

This is used to prepare an IR for insert-rotate after fully unrolling loops.

-arith-to-cggi-quart

Lower arith to cggi dialect and divide each operation into smaller parts.

This pass converts high precision arithmetic operations, i.e. operations on 32 bit integer, into a sequence of lower precision operations, i.e 8b operations. Currently, the pass splits the 32b integer into four 8b integers, using the tensor dialect. These smaller integers are stored in an 16b integer, so that we don’t lose the carry information. This pass converts the arith dialect to the cggi dialect.

Based on the arith-emulate-wide-int pass from the MLIR arith dialect.

General assumption: the first element in the tensor is also the LSB element.

-arith-to-cggi

Lower arith to cggi dialect.

-arith-to-mod-arith

Lower standard arith to mod-arith.

This pass lowers the arith dialect to their mod-arith equivalents.

This pass will transform arith operations to the mod-arith dialect, where the find-mac pass can be used to convert consecutive multiply addition operations into a single operation. In a later pass, these large precision MAC operations (typically 64 or 32-bit) will be lowered into small precision (8 or 4b) operations that can be mapped to CGGI operations.

Options

-modulus : Modulus to use for the mod-arith dialect. If not specified, the pass will use the natural modulus for that integer type

-bgv-to-lwe

Lower bgv to lwe dialect.

This pass lowers the bgv dialect to lwe dialect. Note that some scheme specific ops (e.g., modswitch) that have no direct analogue in the lwe dialect are left unchanged. TODO (#1193): support both “common” and “full” lwe lowering

-cggi-boolean-vectorize

Group different logic gates with the packed API

This pass groups independent logic gates into a single call of the packed operations. Pass is based on the straight-line-vectorizer, but is fundamentally different. This pass combines any type of boolean gates and is not restricted to combining the same type of gate operand.

Pass is intended for the FPT tfhe-rs API, where packed_gates function get a the boolean gates are passed as a string vector and a left and right vector of ciphertexts. Each boolean gates specified in gates is then applied element wise.

let outputs_ct = fpga_key.packed_gates(&gates, &ref_to_ct_lefts, &ref_to_ct_rights);

Options

-parallelism : Parallelism factor for batching. 0 is infinite parallelism

-cggi-decompose-operations

Expands CGGI operations into LWE operations and programmable bootstraps

This pass expands high level CGGI operations (e.g. LUT2, XOR, etc.).

If the option expand-lincomb is set, the expansion will continue into the component LWE scalar operations and a programmable bootstrap operation. Otherwise, the expansion will be stop at the cggi.lut_lincomb level. By default, expand-lincomb is true.

For example, a LUT3 operation is composed of three LWE ciphertext inputs $c, b, a$ (in MSB to LSB ordering) which must be combined via the linear combination $4 * c + 2 * b + a$ before being fed into a programmable bootstrap defined by the lookup table.

This pass supports XOR, LUT2, LUT3, and LutLincomb operations.

Options

-expand-lincomb : Expand lincomb operations to the PBS and scalar level

-cggi-to-jaxite

Lower cggi to jaxite dialect.

-cggi-to-tfhe-rust-bool

Lower cggi to tfhe_rust_bool dialect.

-cggi-to-tfhe-rust

Lower cggi to tfhe_rust dialect.

-ckks-to-lwe

Lower ckks to lwe dialect.

This pass lowers the ckks dialect to lwe dialect. Note that some scheme specific ops (e.g., rescale) that have no direct analogue in the lwe dialect are left unchanged. TODO (#1193): support both “common” and “full” lwe lowering

-collapse-insertion-chains

Collapse chains of extract/insert ops into rotate ops when possible

This pass is a cleanup pass for insert-rotate. That pass sometimes leaves behind a chain of insertion operations like this:

%extracted = tensor.extract %14[%c5] : tensor<16xi16>
%inserted = tensor.insert %extracted into %dest[%c0] : tensor<16xi16>
%extracted_0 = tensor.extract %14[%c6] : tensor<16xi16>
%inserted_1 = tensor.insert %extracted_0 into %inserted[%c1] : tensor<16xi16>
%extracted_2 = tensor.extract %14[%c7] : tensor<16xi16>
%inserted_3 = tensor.insert %extracted_2 into %inserted_1[%c2] : tensor<16xi16>
...
%extracted_28 = tensor.extract %14[%c4] : tensor<16xi16>
%inserted_29 = tensor.insert %extracted_28 into %inserted_27[%c15] : tensor<16xi16>
yield %inserted_29 : tensor<16xi16>

In many cases, this chain will insert into every index of the dest tensor, and the extracted values all come from consistently aligned indices of the same source tensor. In this case, the chain can be collapsed into a single rotate.

Each index used for insertion or extraction must be constant; this may require running --canonicalize or --sccp before this pass to apply folding rules (use --sccp if you need to fold constant through control flow).

-compare-to-sign-rewrite

Rewrites arith.cmpi/arith.cmpf to a math_ext.sign based expression

This pass rewrites arith.cmpi/cmpf %a, %b to some combination of add/mul and sign operations. TODO(#1929): provide detailed description of the expression for each predicate.

Example

Command: heir-opt --compare-to-sign-rewrite tests/Transforms/compare_to_sign_rewrite/doctest.mlir

Input:

func.func @cmpi_sgt(%arg0: i32, %arg1: i32) -> i1 {
  %0 = arith.cmpi sgt, %arg0, %arg1 : i32
  return %0 : i1
}

Output:

module {
  func.func @cmpi_sgt(%arg0: i32, %arg1: i32) -> i1 {
    %0 = arith.sitofp %arg0 : i32 to f32
    %1 = arith.sitofp %arg1 : i32 to f32
    %2 = arith.subf %1, %0 : f32
    %3 = math_ext.sign %2 : f32
    %cst = arith.constant 1.000000e+00 : f32
    %cst_0 = arith.constant 5.000000e-01 : f32
    %4 = arith.addf %3, %cst : f32
    %5 = arith.mulf %4, %cst_0 : f32
    %6 = arith.fptosi %5 : f32 to i1
    return %6 : i1
  }
}

-convert-elementwise-to-affine

This pass lowers ElementwiseMappable operations to Affine loops.

This pass lowers ElementwiseMappable operations over tensors to affine loop nests that instead apply the operation to the underlying scalar values.

Usage: ‘–convert-elementwise-to-affine=convert-ops=arith.mulf ' restrict conversion to mulf op from arith dialect.

‘–convert-elementwise-to-affine=convert-ops=arith.addf,arith.divf convert-dialects=bgv’ restrict conversion to addf and divf ops from arith dialect and all of the ops in bgv dialect.

–convert-elementwise-to-affine=convert-dialects=arith restrict conversion to arith dialect so ops only from arith dialect is processed.

–convert-elementwise-to-affine=convert-ops=arith.addf,arith.mulf restrict conversion only to these two ops - addf and mulf - from arith dialect.

Options

-convert-ops      : comma-separated list of ops to run this pass on 
-convert-dialects : comma-separated list of dialects to run this pass on

-convert-if-to-select

Convert scf.if operations on secret conditions to arith.select operations.

Conversion for If-operations that evaluate secret condition to alternative select operations.

Example

Command: heir-opt --convert-if-to-select tests/Transforms/convert_if_to_select/doctest.mlir

Input:

func.func @secret_condition_with_non_secret_int(%inp: i16, %cond: !secret.secret<i1>) -> !secret.secret<i16> {
  %0 = secret.generic(%inp: i16, %cond: !secret.secret<i1>) {
  ^bb0(%copy_inp: i16, %secret_cond: i1):
    %1 = scf.if %secret_cond -> (i16) {
      %2 = arith.addi %copy_inp, %copy_inp : i16
      scf.yield %2 : i16
    } else {
      scf.yield %copy_inp : i16
    }
    secret.yield %1 : i16
  } -> !secret.secret<i16>
  return %0 : !secret.secret<i16>
}

Output:

module {
  func.func @secret_condition_with_non_secret_int(%arg0: i16, %arg1: !secret.secret<i1>) -> !secret.secret<i16> {
    %0 = secret.generic(%arg0: i16, %arg1: !secret.secret<i1>) {
    ^body(%input0: i16, %input1: i1):
      %1 = arith.addi %input0, %input0 : i16
      %2 = arith.select %input1, %1, %input0 : i16
      secret.yield %2 : i16
    } -> !secret.secret<i16>
    return %0 : !secret.secret<i16>
  }
}

-convert-polynomial-mul-to-ntt

Rewrites polynomial operations to their NTT equivalents

Applies a rewrite pattern to convert polynomial multiplication to the equivalent using the number-theoretic transforms (NTT) when possible.

Polynomial multiplication can be rewritten as polynomial.NTT on each operand, followed by modulo elementwise multiplication of the point-value representation and then the inverse-NTT back to coefficient representation.

-convert-secret-extract-to-static-extract

Convert tensor.extract operations on secret index to static extract operations.

Converts tensor.extract operations that read value at secret index to alternative static tensor.extract operations that extracts value at each index and conditionally selects the value extracted at the secret index.

Note: Running this pass alone does not result in a data-oblivious program; we have to run the --convert-if-to-select pass to the resulting program to convert the secret-dependent If-operation to a Select-operation.

Example

Command: heir-opt --convert-secret-extract-to-static-extract tests/Transforms/convert_secret_extract_to_static_extract/doctest.mlir

Input:

func.func @main(%secretTensor: !secret.secret<tensor<32xi16>>, %secretIndex: !secret.secret<index>) -> !secret.secret<i16> {
  %0 = secret.generic(%secretTensor: !secret.secret<tensor<32xi16>>, %secretIndex: !secret.secret<index>) {
  ^bb0(%tensor: tensor<32xi16>, %index: index):
    %extractedValue = tensor.extract %tensor[%index] : tensor<32xi16>
    secret.yield %extractedValue : i16
  } -> !secret.secret<i16>
  return %0 : !secret.secret<i16>
}

Output:

module {
  func.func @main(%arg0: !secret.secret<tensor<32xi16>>, %arg1: !secret.secret<index>) -> !secret.secret<i16> {
    %c0 = arith.constant 0 : index
    %0 = secret.generic(%arg0: !secret.secret<tensor<32xi16>>, %arg1: !secret.secret<index>) {
    ^body(%input0: tensor<32xi16>, %input1: index):
      %extracted = tensor.extract %input0[%c0] : tensor<32xi16>
      %1 = affine.for %arg2 = 0 to 32 iter_args(%arg3 = %extracted) -> (i16) {
        %2 = arith.cmpi eq, %arg2, %input1 : index
        %extracted_0 = tensor.extract %input0[%arg2] : tensor<32xi16>
        %3 = scf.if %2 -> (i16) {
          scf.yield %extracted_0 : i16
        } else {
          scf.yield %arg3 : i16
        }
        affine.yield %3 : i16
      }
      secret.yield %1 : i16
    } -> !secret.secret<i16>
    return %0 : !secret.secret<i16>
  }
}

-convert-secret-for-to-static-for

Convert secret scf.for ops to affine.for ops with constant bounds.

Conversion for For-operation that evaluate secret bound(s) to alternative affine For-operation with constant bound(s).

It replaces data-dependent bounds with an If-operation to check the bounds, and conditionally execute and yield values from the For-operation’s body. Note: Running this pass alone does not result in a data-oblivious program; we have to run the --convert-if-to-select pass to the resulting program to convert the secret-dependent If-operation to a Select-operation.

Example

Command: heir-opt --convert-secret-for-to-static-for tests/Transforms/convert_secret_for_to_static_for/doctest.mlir

Input:

func.func @main(%secretTensor: !secret.secret<tensor<16xi32>>, %secretLower: !secret.secret<index>, %secretUpper: !secret.secret<index>) -> !secret.secret<i32> {
  %c0 = arith.constant 0 : i32
  %c1 = arith.constant 1 : index
  %0 = secret.generic(%secretTensor: !secret.secret<tensor<16xi32>>, %secretLower: !secret.secret<index>, %secretUpper: !secret.secret<index>) {
  ^bb0(%tensor: tensor<16xi32>, %lower : index, %upper : index ):
    %1 = scf.for %i = %lower to %upper step %c1 iter_args(%arg = %c0) -> (i32) {
      %extracted = tensor.extract %tensor[%i] : tensor<16xi32>
      %sum = arith.addi %extracted, %arg : i32
      scf.yield %sum : i32
    } {lower = 0, upper = 16}
    secret.yield %1 : i32
  } -> !secret.secret<i32>
  return %0 : !secret.secret<i32>
}

Output:

module {
  func.func @main(%arg0: !secret.secret<tensor<16xi32>>, %arg1: !secret.secret<index>, %arg2: !secret.secret<index>) -> !secret.secret<i32> {
    %c0_i32 = arith.constant 0 : i32
    %0 = secret.generic(%arg0: !secret.secret<tensor<16xi32>>, %arg1: !secret.secret<index>, %arg2: !secret.secret<index>) {
    ^body(%input0: tensor<16xi32>, %input1: index, %input2: index):
      %1 = affine.for %arg3 = 0 to 16 iter_args(%arg4 = %c0_i32) -> (i32) {
        %2 = arith.cmpi sge, %arg3, %input1 : index
        %3 = arith.cmpi slt, %arg3, %input2 : index
        %4 = arith.andi %2, %3 : i1
        %5 = scf.if %4 -> (i32) {
          %extracted = tensor.extract %input0[%arg3] : tensor<16xi32>
          %6 = arith.addi %extracted, %arg4 : i32
          scf.yield %6 : i32
        } else {
          scf.yield %arg4 : i32
        }
        affine.yield %5 : i32
      } {lower = 0 : i64, upper = 16 : i64}
      secret.yield %1 : i32
    } -> !secret.secret<i32>
    return %0 : !secret.secret<i32>
  }
}

Options

-convert-all-scf-for : If true, convert all scf.for ops to affine.for, not just those with secret bounds.

-convert-secret-insert-to-static-insert

Convert tensor.insert operations on secret index to static insert operations.

Converts tensor.insert operations that write to secret index to alternative static tensor.insert operations that inserts the inserted value at each index and conditionally selects the newly produced tensor that contains the value at the secret index.

Note: Running this pass alone does not result in a data-oblivious program; we have to run the --convert-if-to-select pass to the resulting program to convert the secret-dependent If-operation to a Select-operation.

Example

Command: heir-opt --convert-secret-insert-to-static-insert tests/Transforms/convert_secret_insert_to_static_insert/doctest.mlir

Input:

func.func @main(%secretTensor: !secret.secret<tensor<32xi16>>, %secretIndex: !secret.secret<index>) -> !secret.secret<tensor<32xi16>> {
  %c0 = arith.constant 0 : i16
  %0 = secret.generic(%secretTensor: !secret.secret<tensor<32xi16>>, %secretIndex: !secret.secret<index>) {
  ^bb0(%tensor: tensor<32xi16>, %index: index):
    // Violation: tensor.insert writes value at secret index
    %inserted = tensor.insert %c0 into %tensor[%index] : tensor<32xi16>
    secret.yield %inserted : tensor<32xi16>
  } -> !secret.secret<tensor<32xi16>>
  return %0 : !secret.secret<tensor<32xi16>>
}

Output:

module {
  func.func @main(%arg0: !secret.secret<tensor<32xi16>>, %arg1: !secret.secret<index>) -> !secret.secret<tensor<32xi16>> {
    %c0_i16 = arith.constant 0 : i16
    %0 = secret.generic(%arg0: !secret.secret<tensor<32xi16>>, %arg1: !secret.secret<index>) {
    ^body(%input0: tensor<32xi16>, %input1: index):
      %1 = affine.for %arg2 = 0 to 32 iter_args(%arg3 = %input0) -> (tensor<32xi16>) {
        %2 = arith.cmpi eq, %arg2, %input1 : index
        %inserted = tensor.insert %c0_i16 into %arg3[%arg2] : tensor<32xi16>
        %3 = scf.if %2 -> (tensor<32xi16>) {
          scf.yield %inserted : tensor<32xi16>
        } else {
          scf.yield %arg3 : tensor<32xi16>
        }
        affine.yield %3 : tensor<32xi16>
      }
      secret.yield %1 : tensor<32xi16>
    } -> !secret.secret<tensor<32xi16>>
    return %0 : !secret.secret<tensor<32xi16>>
  }
}

-convert-secret-while-to-static-for

Convert secret scf.while ops to affine.for ops that have constant bounds.

Convert scf.while with a secret condition to affine.for with constant bounds. It replaces the scf.condition operation found in the scf.while loop with an scf.if operation that conditionally executes operations in the while operation’s body and yields values.

A “max_iter” attribute should be specified as part of the secret-dependent scf.while operation to successfully transform to a secret-independent affine.for operation. This attribute determines the maximum number of iterations for the new affine.for operation.

Note: Running this pass alone does not result in a data-oblivious program; we have to run the --convert-if-to-select pass to the resulting program to convert the secret-dependent If-operation to a Select-operation.

Example

Command: heir-opt --convert-secret-while-to-static-for tests/Transforms/convert_secret_while_to_static_for/doctest.mlir

Input:

func.func @main(%secretInput: !secret.secret<i16>) -> !secret.secret<i16> {
  %c100 = arith.constant 100 : i16
  %0 = secret.generic(%secretInput: !secret.secret<i16>) {
  ^bb0(%input: i16):
    %1 = scf.while (%arg1 = %input) : (i16) -> i16 {
      %2 = arith.cmpi sgt, %arg1, %c100 : i16
      scf.condition(%2) %arg1 : i16
    } do {
    ^bb0(%arg1: i16):
      %3 = arith.muli %arg1, %arg1 : i16
      scf.yield %3 : i16
    } attributes {max_iter = 16 : i64}
    secret.yield %1 : i16
  } -> !secret.secret<i16>
  return %0 : !secret.secret<i16>
}

Output:

module {
  func.func @main(%arg0: !secret.secret<i16>) -> !secret.secret<i16> {
    %c100_i16 = arith.constant 100 : i16
    %0 = secret.generic(%arg0: !secret.secret<i16>) {
    ^body(%input0: i16):
      %1 = affine.for %arg1 = 0 to 16 iter_args(%arg2 = %input0) -> (i16) {
        %2 = arith.cmpi sgt, %arg2, %c100_i16 : i16
        %3 = scf.if %2 -> (i16) {
          %4 = arith.muli %arg2, %arg2 : i16
          scf.yield %4 : i16
        } else {
          scf.yield %arg2 : i16
        }
        affine.yield %3 : i16
      } {max_iter = 16 : i64}
      secret.yield %1 : i16
    } -> !secret.secret<i16>
    return %0 : !secret.secret<i16>
  }
}

-convert-tensor-to-scalars

Effectively ‘unrolls’ tensors of static shape to scalars.

This pass will convert a static-shaped tensor type to a TypeRange containing product(dim) copies of the element type of the tensor. This pass currently includes two patterns:

  1. It converts tensor.from_elements operations to the corresponding scalar inputs.
  2. It converts tensor.insert operations by updating the ValueRange corresponding to the converted input and updating it with the scalar to be inserted.

It also applies folders greedily to simplify, e.g., extract(from_elements).

Note: The pass is designed to be run on an IR, where the only operations with tensor typed operands are tensor “management” operations such as insert/extract, with all other operations (e.g., arith operations) already taking (extracted) scalar inputs. For example, an IR where elementwise operations have been converted to scalar operations via --convert-elementwise-to-affine.

The pass might insert new tensor.from_elements operations or manually create the scalar ValueRange via inserting tensor.extract operations if any operations remain that operate on tensors. The pass currently applies irrespective of tensor size, i.e., might be very slow for large tensors.

TODO (#1023): Extend this pass to support more tensor operations, e.g., tensor.slice

Options

-max-size : Limits `unrolling` to tensors with at most max-size elements

-convert-to-ciphertext-semantics

Converts programs with tensor semantics to ciphertext semantics

This pass performs two inherently intertwined transformations:

  1. Convert a program from tensor semantics to ciphertext semantics, explained below.
  2. Implement ops defined on tensor-semantic types in terms of ops defined on ciphertext-semantic types.

A program is defined to have tensor semantics if the tensor-typed values are manipulated according to standard MLIR tensor operations and semantics.

A program is defined to have ciphertext semantics if the tensor-typed values correspond to tensors of FHE ciphertexts, where the last dimension of the tensor type is the number of ciphertext slots.

For example, a tensor of type tensor<32x32xi16> with tensor semantics might be converted by this pass, depending on the pass options, to a single ciphertext-semantics tensor<65536xi16>. A larger tensor might, depending on the layout chosen by earlier passes, be converted to a tensor<4x32768xi16>, where the trailing dimension corresponds to the number of slots in the ciphertext.

Tensors with ciphertext semantics can be thought of as an intermediate step between lowering from tensor types with tensor semantics to concrete lwe dialect ciphertext types in a particular FHE scheme. Having this intermediate step is useful because some optimizations are easier to implement, and can be implemented more generically, in the abstract FHE computational model where the data types are large tensors, and the operations are SIMD additions, multiplications, and cyclic rotations.

Function arguments and return values are annotated with the original tensor type in the secret.original_type attribute. This enables later lowerings to implement appropriate encoding and decoding routines for FHE schemes.

The second role of this pass is to implement FHE kernels for various high-level tensor operations, such as linalg.matvec. This must happen at the same time as the type conversion because the high-level ops like linalg.matvec are not well-defined on ciphertext-semantic tensors, while their implementation as SIMD/rotation ops are not well-defined on tensor-semantic tensors.

Example

Command: heir-opt tests/Transforms/convert_to_ciphertext_semantics/doctest.mlir --convert-to-ciphertext-semantics=ciphertext-size=4

Input:

// A 2x2 matvec with a plaintext matrix is lowered via the Halevi-Shoup
// diagonal packing/kernel.

#kernel = #secret.kernel<name = "MatvecDiagonal", force = false>
#layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : ct = 0 and (-i0 + slot) mod 4 = 0 and 0 <= i0 < 4 and 0 <= slot < 4 }">
#layout1 = #tensor_ext.layout<"{ [i0, i1] -> [ct, slot] : (i0 - i1 + ct) mod 4 = 0 and (-i0 + slot) mod 4 = 0 and 0 <= i0 < 4 and 0 <= i1 < 4 and 0 <= ct < 4 and 0 <= slot < 4 }">

func.func @matvec(
    %arg0: !secret.secret<tensor<4xf32>> {tensor_ext.layout = #layout}
) -> (!secret.secret<tensor<4xf32>> {tensor_ext.layout = #layout}) {
  %cst = arith.constant dense<0.000000e+00> : tensor<4xf32>
  %cst_0 = arith.constant dense<2.0> : tensor<4x4xf32>
  %0 = secret.generic(%arg0: !secret.secret<tensor<4xf32>> {tensor_ext.layout = #layout}) {
  ^body(%input0: tensor<4xf32>):
    %1 = tensor_ext.assign_layout %cst_0 {layout = #layout1, tensor_ext.layout = #layout1} : tensor<4x4xf32>
    %2 = tensor_ext.assign_layout %cst {layout = #layout, tensor_ext.layout = #layout} : tensor<4xf32>
    %3 = linalg.matvec {secret.kernel = #kernel, tensor_ext.layout = #layout}
          ins(%1, %input0 : tensor<4x4xf32>, tensor<4xf32>)
          outs(%2 : tensor<4xf32>) -> tensor<4xf32>
    secret.yield %3 : tensor<4xf32>
  } -> (!secret.secret<tensor<4xf32>> {tensor_ext.layout = #layout})
  return %0 : !secret.secret<tensor<4xf32>>
}

Output:

#layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : ct = 0 and (-i0 + slot) mod 4 = 0 and 0 <= i0 < 4 and 0 <= slot < 4 }">
#original_type = #tensor_ext.original_type<originalType = tensor<4xf32>, layout = #layout>
module {
  func.func @matvec(%arg0: !secret.secret<tensor<1x4xf32>> {tensor_ext.original_type = #original_type}) -> (!secret.secret<tensor<1x4xf32>> {tensor_ext.original_type = #original_type}) {
    %c-2 = arith.constant -2 : index
    %c2 = arith.constant 2 : index
    %cst = arith.constant 0.000000e+00 : f32
    %cst_0 = arith.constant dense<0.000000e+00> : tensor<1x4xf32>
    %cst_1 = arith.constant 2.000000e+00 : f32
    %c4 = arith.constant 4 : index
    %c1 = arith.constant 1 : index
    %c3 = arith.constant 3 : index
    %c0 = arith.constant 0 : index
    %cst_2 = arith.constant dense<0.000000e+00> : tensor<4x4xf32>
    %0 = secret.generic(%arg0: !secret.secret<tensor<1x4xf32>>) {
    ^body(%input0: tensor<1x4xf32>):
      %1 = scf.for %arg1 = %c0 to %c4 step %c1 iter_args(%arg2 = %cst_2) -> (tensor<4x4xf32>) {
        %18 = scf.for %arg3 = %c0 to %c4 step %c1 iter_args(%arg4 = %arg2) -> (tensor<4x4xf32>) {
          %inserted = tensor.insert %cst_1 into %arg4[%arg1, %arg3] : tensor<4x4xf32>
          scf.yield %inserted : tensor<4x4xf32>
        }
        scf.yield %18 : tensor<4x4xf32>
      }
      %2 = scf.for %arg1 = %c0 to %c4 step %c1 iter_args(%arg2 = %cst_0) -> (tensor<1x4xf32>) {
        %inserted = tensor.insert %cst into %arg2[%c0, %arg1] : tensor<1x4xf32>
        scf.yield %inserted : tensor<1x4xf32>
      }
      %extracted_slice = tensor.extract_slice %1[%c0, 0] [1, 4] [1, 1] : tensor<4x4xf32> to tensor<1x4xf32>
      %3 = tensor_ext.rotate %extracted_slice, %c0 : tensor<1x4xf32>, index
      %4 = arith.mulf %3, %input0 : tensor<1x4xf32>
      %extracted_slice_3 = tensor.extract_slice %1[%c1, 0] [1, 4] [1, 1] : tensor<4x4xf32> to tensor<1x4xf32>
      %5 = tensor_ext.rotate %extracted_slice_3, %c0 : tensor<1x4xf32>, index
      %6 = tensor_ext.rotate %input0, %c1 : tensor<1x4xf32>, index
      %7 = arith.mulf %5, %6 : tensor<1x4xf32>
      %8 = arith.addf %4, %7 : tensor<1x4xf32>
      %9 = tensor_ext.rotate %8, %c0 : tensor<1x4xf32>, index
      %extracted_slice_4 = tensor.extract_slice %1[%c2, 0] [1, 4] [1, 1] : tensor<4x4xf32> to tensor<1x4xf32>
      %10 = tensor_ext.rotate %extracted_slice_4, %c-2 : tensor<1x4xf32>, index
      %11 = arith.mulf %10, %input0 : tensor<1x4xf32>
      %extracted_slice_5 = tensor.extract_slice %1[%c3, 0] [1, 4] [1, 1] : tensor<4x4xf32> to tensor<1x4xf32>
      %12 = tensor_ext.rotate %extracted_slice_5, %c-2 : tensor<1x4xf32>, index
      %13 = arith.mulf %12, %6 : tensor<1x4xf32>
      %14 = arith.addf %11, %13 : tensor<1x4xf32>
      %15 = tensor_ext.rotate %14, %c2 : tensor<1x4xf32>, index
      %16 = arith.addf %9, %15 : tensor<1x4xf32>
      %17 = arith.addf %16, %2 : tensor<1x4xf32>
      secret.yield %17 : tensor<1x4xf32>
    } -> !secret.secret<tensor<1x4xf32>>
    return %0 : !secret.secret<tensor<1x4xf32>>
  }
}

Options

-ciphertext-size : Power of two length of the ciphertexts the data is packed in.

-drop-unit-dims

Drops unit dimensions from linalg ops.

This pass converts linalg whose operands have unit dimensions in their types to specialized ops that drop these unit dimensions.

For example, a linalg.matmul whose RHS has type tensor<32x1xi32> is converted to a linalg.matvec op on the underlying tensor<32xi32>.

-emit-c-interface

Adds llvm.emit_c_interface to each public function.

-expand-copy

Expands memref.copy ops to explicit affine loads and stores

This pass removes memref copy operations by expanding them to affine loads and stores. This pass introduces affine loops over the dimensions of the MemRef, so must be run prior to any affine loop unrolling in a pipeline.

Example

Command: heir-opt --expand-copy tests/Transforms/expand_copy/doctest.mlir

Input:

func.func @memref_copy() {
  %alloc = memref.alloc() : memref<2x3xi32>
  %alloc_0 = memref.alloc() : memref<2x3xi32>
  memref.copy %alloc, %alloc_0 : memref<2x3xi32> to memref<2x3xi32>
  return
}

Output:

module {
  func.func @memref_copy() {
    %alloc = memref.alloc() : memref<2x3xi32>
    %alloc_0 = memref.alloc() : memref<2x3xi32>
    affine.for %arg0 = 0 to 2 {
      affine.for %arg1 = 0 to 3 {
        %0 = affine.load %alloc[%arg0, %arg1] : memref<2x3xi32>
        affine.store %0, %alloc_0[%arg0, %arg1] : memref<2x3xi32>
      }
    }
    return
  }
}

Options

-disable-affine-loop : Use this to control to disable using affine loops

-extract-loop-body

Extracts logic of a loop bodies into functions.

This pass extracts logic in the inner body of for loops into functions.

This pass requires that tensors are lowered to memref. It expects that a loop body contains a number of affine.load statements used as inputs to the extracted function, and a single affine.store used as the extracted function’s output.

Input

module {
  func.func @loop_body() {
    %c-128_i8 = arith.constant -128 : i8
    %c127_i8 = arith.constant 127 : i8
    %alloc_7 = memref.alloc() {alignment = 64 : i64} : memref<25x20x8xi8>
    affine.for %arg1 = 0 to 25 {
      affine.for %arg2 = 0 to 20 {
        affine.for %arg3 = 0 to 8 {
          %98 = affine.load %alloc_6[%arg1, %arg2, %arg3] : memref<25x20x8xi8>
          %99 = arith.cmpi slt, %arg0, %c-128_i8 : i8
          %100 = arith.select %99, %c-128_i8, %arg0 : i8
          %101 = arith.cmpi sgt, %arg0, %c127_i8 : i8
          %102 = arith.select %101, %c127_i8, %100 : i8
          affine.store %102, %alloc_7[%arg1, %arg2, %arg3] : memref<25x20x8xi8>
        }
      }
    }
  }
}

Output

module {
  func.func @loop_body() {
    %alloc_7 = memref.alloc() {alignment = 64 : i64} : memref<25x20x8xi8>
    affine.for %arg1 = 0 to 25 {
      affine.for %arg2 = 0 to 20 {
        affine.for %arg3 = 0 to 8 {
          %98 = affine.load %alloc_6[%arg1, %arg2, %arg3] : memref<25x20x8xi8>
          %102 = func.call @__for_loop(%98) : (i8) -> i8
          affine.store %102, %alloc_7[%arg1, %arg2, %arg3] : memref<25x20x8xi8>
        }
      }
    }
  }
  func.func private @__for_loop(%arg0: i8) -> i8 {
    %c-128_i8 = arith.constant -128 : i8
    %c127_i8 = arith.constant 127 : i8
    %99 = arith.cmpi slt, %arg0, %c-128_i8 : i8
    %100 = arith.select %99, %c-128_i8, %arg0 : i8
    %101 = arith.cmpi sgt, %arg0, %c127_i8 : i8
    %102 = arith.select %101, %c127_i8, %100 : i8
    return %102 : i8
  }
}

Options

-min-loop-size : Use this to control the minimum loop size to apply this pass
-min-body-size : Use this to control the minimum loop body size to apply this pass

-fold-constant-tensors

This pass folds any constant tensors.

This pass folds tensor operations on constants to new constants.

The following folders are supported:

  • tensor.insert of a constant tensor
  • tensor.collapse_shape of a constant or empty tensor
  • tensor.extract_slice of a splat to a splat of the new shape

-fold-convert-layout-into-assign-layout

Merges tensor_ext.convert_layout ops into preceding tensor_ext.assign_layout ops

A tensor_ext.assign_layout op corresponds to an encoding of a cleartext into a plaintext or ciphertext. If this is immediately followed by a tensor_ext.convert_layout op, then one can just change the initial encoding to correspond to the result of the conversion.

If the result of an assign_layout has multiple subsequent convert_layout ops, then they are folded into multiple assign_layout ops applied to the same cleartext.

-fold-plaintext-masks

Apply folding rules for tensor masking operations

This pass applies a set of folding rules to optimize ciphertext-plaintext masking operations that occur on ciphertext-semantic tensors.

This typically corresponds to applications of arith.muli or arith.mulf where one operand is a constant tensor consisting of 1’s and 0’s. Because these apply even when the operand tensors are not specifically ciphertext-semantic tensors, this pass can run on any IR and it will still produce semantically correct results.

Example

Command: heir-opt tests/Transforms/fold_plaintext_masks/doctest.mlir --fold-plaintext-masks

Input:

func.func @example(%arg0: tensor<6xi32>) -> tensor<6xi32> {
  %cst_1 = arith.constant dense<[1, 1, 1, 0, 0, 0]> : tensor<6xi32>
  %cst_2 = arith.constant dense<[0, 1, 1, 1, 1, 1]> : tensor<6xi32>
  %1 = arith.muli %arg0, %cst_1 : tensor<6xi32>
  %2 = arith.muli %1, %cst_2 : tensor<6xi32>
  return %2 : tensor<6xi32>
}

Output:

module {
  func.func @example(%arg0: tensor<6xi32>) -> tensor<6xi32> {
    %cst = arith.constant dense<[0, 1, 1, 0, 0, 0]> : tensor<6xi32>
    %0 = arith.muli %arg0, %cst : tensor<6xi32>
    return %0 : tensor<6xi32>
  }
}

-forward-insert-to-extract

Forward inserts to extracts within a single block

This pass is similar to forward-store-to-load pass where store ops are forwarded load ops; here instead tensor.insert ops are forwarded to tensor.extract ops.

Does not support complex control flow within a block, nor ops with arbitrary subregions.

-forward-store-to-load

Forward stores to loads within a single block

This pass is a simplified version of mem2reg and similar passes. It analyzes an operation, finding all basic blocks within that op that have memrefs whose stores can be forwarded to loads.

Does not support complex control flow within a block, nor ops with arbitrary subregions.

-full-loop-unroll

Fully unroll all loops

Scan the IR for affine.for loops and unroll them all.

-generate-param-bfv

Generate BFV Scheme Parameter

The pass generates the BFV scheme parameter using a given noise model.

There are four noise models available:

  • bfv-noise-by-bound-coeff-average-case or bfv-noise-kpz21
  • bfv-noise-by-bound-coeff-worst-case
  • bfv-noise-by-variance-coeff or bfv-noise-bmcm23
  • bfv-noise-canon-emb

To use public-key encryption/secret-key encryption in the model, the option usePublicKey could be set accordingly.

The first two models are taken from KPZ21, and they work by bounding the coefficient embedding of the ciphertexts. The difference of the two models is expansion factor used for multiplication of the coefficients, the first being $2 \sqrt{N}$ ($4 \sqrt{N}$ in some special cases) and the second being $N$.

The third model is taken from BMCM23. It works by tracking the variance of the coefficient embedding of the ciphertexts. This gives a much tighter noise estimate for independent ciphertext input, but may give underestimation for dependent ciphertext input. See the paper for more details. One possible explanation of the underestimation is this paper

The last model is adapted from MMLGA22 with mixes from BMCM23 and KPZ21. It uses the canonical embedding to bound the critical quantity of a ciphertext that defines whether c can be decrypted correctly.

This pass then generates the moduli chain consisting of primes of bits specified by the mod-bits field.

Usually for B/FV mod-bits is set to 60. But when machine word size is small, users may also want to set it to 57.

This pass relies on the presence of the mgmt dialect ops to model relinearize, and it relies on mgmt.mgmt attribute to determine the ciphertext level/dimension. These ops and attributes can be added by a pass like --secret-insert-mgmt-bgv and --annotate-mgmt.

User can provide custom scheme parameters by annotating bgv::SchemeParamAttr at the module level. Note that we reuse bgv::SchemeParamAttr for BFV.

Example

Command: heir-opt --generate-param-bfv tests/Transforms/generate_param_bfv/doctest.mlir

Input:

module {
  func.func @add(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) {
    %0 = secret.generic(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) attrs = {arg0 = {mgmt.mgmt = #mgmt.mgmt<level = 0>}} {
    ^body(%input0: i16):
      %1 = arith.addi %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : i16
      secret.yield %1 : i16
    } -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<i16>
  }
}

Output:

module attributes {bgv.schemeParam = #bgv.scheme_param<logN = 12, Q = [2147565569], P = [2147573761], plaintextModulus = 65537>} {
  func.func @add(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) {
    %0 = secret.generic(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) attrs = {arg0 = {mgmt.mgmt = #mgmt.mgmt<level = 0>}} {
    ^body(%input0: i16):
      %1 = arith.addi %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : i16
      secret.yield %1 : i16
    } -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<i16>
  }
}

Options

-model                         : Noise model to validate against.
-mod-bits                      : Default number of bits for all prime coefficient modulusto use for the ciphertext space.
-slot-number                   : Minimum number of slots for parameter generation.
-plaintext-modulus             : Plaintext modulus.
-use-public-key                : If true, uses a public key for encryption.
-encryption-technique-extended : If true, uses EXTENDED encryption technique for encryption. (See https://ia.cr/2022/915)

-generate-param-bgv

Generate BGV Scheme Parameter using a given noise model

The pass generates the BGV scheme parameter using a given noise model.

There are four noise models available:

  • bgv-noise-by-bound-coeff-average-case or bgv-noise-kpz21
  • bgv-noise-by-bound-coeff-worst-case
  • bgv-noise-by-variance-coeff or bgv-noise-mp24
  • bgv-noise-mono

To use public-key encryption/secret-key encryption in the model, the option usePublicKey could be set accordingly.

The first two models are taken from KPZ21, and they work by bounding the coefficient embedding of the ciphertexts. The difference of the two models is expansion factor used for multiplication of the coefficients, the first being $2 \sqrt{N}$ ($4 \sqrt{N}$ in some special cases) and the second being $N$.

The third model is taken from MP24. It works by tracking the variance of the coefficient embedding of the ciphertexts. This gives a more accurate noise estimate, but it may give underestimates in some cases. See the paper for more details. One possible explanation of the underestimation is this paper.

The last model is taken from MMLGA22. It uses the canonical embedding to bound the critical quantity of a ciphertext that defines whether c can be decrypted correctly. According to the authors they achieve more accurate and better bounds than KPZ21. See the paper for more details.

This pass relies on the presence of the mgmt dialect ops to model relinearize/modreduce, and it relies on mgmt.mgmt attribute to determine the ciphertext level/dimension. These ops and attributes can be added by a pass like --secret-insert-mgmt-bgv.

User can provide custom scheme parameters by annotating bgv::SchemeParamAttr at the module level.

Example

Command: heir-opt --generate-param-bgv tests/Transforms/generate_param_bgv/doctest.mlir

Input:

module {
  func.func @add(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) {
    %0 = secret.generic(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) attrs = {arg0 = {mgmt.mgmt = #mgmt.mgmt<level = 0>}} {
    ^body(%input0: i16):
      %1 = arith.addi %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : i16
      secret.yield %1 : i16
    } -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<i16>
  }
}

Output:

module attributes {bgv.schemeParam = #bgv.scheme_param<logN = 12, Q = [4294991873], P = [4295049217], plaintextModulus = 65537>} {
  func.func @add(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) {
    %0 = secret.generic(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) attrs = {arg0 = {mgmt.mgmt = #mgmt.mgmt<level = 0>}} {
    ^body(%input0: i16):
      %1 = arith.addi %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : i16
      secret.yield %1 : i16
    } -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<i16>
  }
}

Options

-model                         : Noise model to validate against.
-plaintext-modulus             : Plaintext modulus.
-slot-number                   : Minimum number of slots for parameter generation.
-use-public-key                : If true, uses a public key for encryption.
-encryption-technique-extended : If true, uses EXTENDED encryption technique for encryption. (See https://ia.cr/2022/915)

-generate-param-ckks

Generate CKKS Scheme Parameter

The pass generates the CKKS scheme parameter.

The pass asks the user to provide the number of bits for the first modulus and scaling modulus. The default values are 55 and 45, respectively. Then the pass generates the moduli chain using the provided values.

This pass relies on the presence of the mgmt dialect ops to model relinearize/modreduce, and it relies on mgmt.mgmt attribute to determine the ciphertext level/dimension. These ops and attributes can be added by a pass like --secret-insert-mgmt-<scheme> and --annotate-mgmt.

User can provide custom scheme parameters by annotating bgv::SchemeParamAttr at the module level.

Example

Command: heir-opt --generate-param-ckks tests/Transforms/generate_param_ckks/doctest.mlir

Input:

module {
  func.func @add(%arg0: !secret.secret<f16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) -> (!secret.secret<f16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) {
    %0 = secret.generic(%arg0: !secret.secret<f16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) attrs = {arg0 = {mgmt.mgmt = #mgmt.mgmt<level = 0>}} {
    ^body(%input0: f16):
      %1 = arith.addf %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : f16
      secret.yield %1 : f16
    } -> (!secret.secret<f16> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<f16>
  }
}

Output:

module attributes {ckks.schemeParam = #ckks.scheme_param<logN = 13, Q = [36028797019389953], P = [36028797019488257], logDefaultScale = 45>} {
  func.func @add(%arg0: !secret.secret<f16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) -> (!secret.secret<f16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) {
    %0 = secret.generic(%arg0: !secret.secret<f16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) attrs = {arg0 = {mgmt.mgmt = #mgmt.mgmt<level = 0>}} {
    ^body(%input0: f16):
      %1 = arith.addf %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : f16
      secret.yield %1 : f16
    } -> (!secret.secret<f16> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<f16>
  }
}

Options

-slot-number                   : Minimum number of slots for parameter generation.
-first-mod-bits                : Default number of bits of the first prime coefficient modulus to use for the ciphertext space.
-scaling-mod-bits              : Default number of bits of the scaling prime coefficient modulus to use for the ciphertext space.
-use-public-key                : If true, uses a public key for encryption.
-encryption-technique-extended : If true, uses EXTENDED encryption technique for encryption. (See https://ia.cr/2022/915)
-input-range                   : The range of the plaintexts for input ciphertexts for the CKKS scheme; default to [-1, 1]. For other ranges like [-D, D], use D.

-implement-rotate-and-reduce

Implement tensor_ext.rotate_and_reduce ops with baby-steps / giant-steps

This pass converts tensor_ext.rotate_and_reduce ops into a sequence of arithmetic operations and tensor_ext.rotate ops, aiming to minimize the number of ciphertext rotation operations using a Baby-Steps / Giant-Steps approach.

A tensor_ext.rotate_and_reduce op computes the reduction of rotated tensors in the form \sum_{i = 0}^{n} P(i) \cdot rotate(v, T*i) where T is some period of rotation. The naive approach would compute n rotations of the ciphertext v. The Baby-Steps / Giant-Steps approach from Faster Homomorphic Linear Transformations in HElib can compute the sum with O(sqrt(n)) ciphertext rotations instead by evaluating the sum with the following expression

$$ \sum_{i = 0}^{n} P(i) \cdot rotate(v, Ti) = \sum_{j = 0}^{\sqrt{n}} \sum_{k = 0}^{\sqrt{n}} P(j + gk) rotate(v, T(j + gk)) = \sum_{j = 0}^{\sqrt{n}} rotate( \sum_{k = 0}^{\sqrt{n}} rotate(P(j + gk), -gk) rotate(v, T*j) , -gk) $$

This approach uses \sqrt{n} ciphertext rotations of v in the inner sum (the baby steps) and then \sqrt{n} ciphertext rotations of the partial sums (the giant steps) to compute the full sum.

The input IR must have tensors that correspond to plaintexts or ciphertexts.

Example

Command: heir-opt --implement-rotate-and-reduce --canonicalize --cse --sccp tests/Dialect/TensorExt/Transforms/implement_rotate_and_reduce.mlir

Input:

// Giant steps (chunked in four) will also need 3 rotations to align the sums.
// Each giant step consists of 4 plaintext extractions. muls, and rotates

// Baby step giant step should reduce the number of ciphertext rotations to 3 (shifts of 0, 1, 2, 3)
// First chunk of 4 baby steps is interleaved with the initial rotations.

// Plaintexts are all rotated by a fixed amount and multiplied by the baby step ciphertexts
// The result is shifted back to the correct position



func.func @test_halevi_shoup_reduction(%0: tensor<16xi32>, %1: tensor<16x16xi32>) -> tensor<16xi32> {
  %2 = tensor_ext.rotate_and_reduce %0, %1 {period = 1 : index, steps = 16 : index} : (tensor<16xi32>, tensor<16x16xi32>) -> tensor<16xi32>
  return %2 : tensor<16xi32>
}

Output:

module {
  func.func @test_halevi_shoup_reduction(%arg0: tensor<16xi32>, %arg1: tensor<16x16xi32>) -> tensor<16xi32> {
    %c1 = arith.constant 1 : index
    %c2 = arith.constant 2 : index
    %c3 = arith.constant 3 : index
    %c4 = arith.constant 4 : index
    %c8 = arith.constant 8 : index
    %c12 = arith.constant 12 : index
    %extracted_slice = tensor.extract_slice %arg1[0, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %0 = arith.muli %extracted_slice, %arg0 : tensor<16xi32>
    %extracted_slice_0 = tensor.extract_slice %arg1[1, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %1 = tensor_ext.rotate %arg0, %c1 : tensor<16xi32>, index
    %2 = arith.muli %extracted_slice_0, %1 : tensor<16xi32>
    %3 = arith.addi %0, %2 : tensor<16xi32>
    %extracted_slice_1 = tensor.extract_slice %arg1[2, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %4 = tensor_ext.rotate %arg0, %c2 : tensor<16xi32>, index
    %5 = arith.muli %extracted_slice_1, %4 : tensor<16xi32>
    %6 = arith.addi %3, %5 : tensor<16xi32>
    %extracted_slice_2 = tensor.extract_slice %arg1[3, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %7 = tensor_ext.rotate %arg0, %c3 : tensor<16xi32>, index
    %8 = arith.muli %extracted_slice_2, %7 : tensor<16xi32>
    %9 = arith.addi %6, %8 : tensor<16xi32>
    %extracted_slice_3 = tensor.extract_slice %arg1[4, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %10 = tensor_ext.rotate %extracted_slice_3, %c12 : tensor<16xi32>, index
    %11 = arith.muli %10, %arg0 : tensor<16xi32>
    %extracted_slice_4 = tensor.extract_slice %arg1[5, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %12 = tensor_ext.rotate %extracted_slice_4, %c12 : tensor<16xi32>, index
    %13 = arith.muli %12, %1 : tensor<16xi32>
    %14 = arith.addi %11, %13 : tensor<16xi32>
    %extracted_slice_5 = tensor.extract_slice %arg1[6, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %15 = tensor_ext.rotate %extracted_slice_5, %c12 : tensor<16xi32>, index
    %16 = arith.muli %15, %4 : tensor<16xi32>
    %17 = arith.addi %14, %16 : tensor<16xi32>
    %extracted_slice_6 = tensor.extract_slice %arg1[7, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %18 = tensor_ext.rotate %extracted_slice_6, %c12 : tensor<16xi32>, index
    %19 = arith.muli %18, %7 : tensor<16xi32>
    %20 = arith.addi %17, %19 : tensor<16xi32>
    %21 = tensor_ext.rotate %20, %c4 : tensor<16xi32>, index
    %22 = arith.addi %9, %21 : tensor<16xi32>
    %extracted_slice_7 = tensor.extract_slice %arg1[8, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %23 = tensor_ext.rotate %extracted_slice_7, %c8 : tensor<16xi32>, index
    %24 = arith.muli %23, %arg0 : tensor<16xi32>
    %extracted_slice_8 = tensor.extract_slice %arg1[9, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %25 = tensor_ext.rotate %extracted_slice_8, %c8 : tensor<16xi32>, index
    %26 = arith.muli %25, %1 : tensor<16xi32>
    %27 = arith.addi %24, %26 : tensor<16xi32>
    %extracted_slice_9 = tensor.extract_slice %arg1[10, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %28 = tensor_ext.rotate %extracted_slice_9, %c8 : tensor<16xi32>, index
    %29 = arith.muli %28, %4 : tensor<16xi32>
    %30 = arith.addi %27, %29 : tensor<16xi32>
    %extracted_slice_10 = tensor.extract_slice %arg1[11, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %31 = tensor_ext.rotate %extracted_slice_10, %c8 : tensor<16xi32>, index
    %32 = arith.muli %31, %7 : tensor<16xi32>
    %33 = arith.addi %30, %32 : tensor<16xi32>
    %34 = tensor_ext.rotate %33, %c8 : tensor<16xi32>, index
    %35 = arith.addi %22, %34 : tensor<16xi32>
    %extracted_slice_11 = tensor.extract_slice %arg1[12, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %36 = tensor_ext.rotate %extracted_slice_11, %c4 : tensor<16xi32>, index
    %37 = arith.muli %36, %arg0 : tensor<16xi32>
    %extracted_slice_12 = tensor.extract_slice %arg1[13, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %38 = tensor_ext.rotate %extracted_slice_12, %c4 : tensor<16xi32>, index
    %39 = arith.muli %38, %1 : tensor<16xi32>
    %40 = arith.addi %37, %39 : tensor<16xi32>
    %extracted_slice_13 = tensor.extract_slice %arg1[14, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %41 = tensor_ext.rotate %extracted_slice_13, %c4 : tensor<16xi32>, index
    %42 = arith.muli %41, %4 : tensor<16xi32>
    %43 = arith.addi %40, %42 : tensor<16xi32>
    %extracted_slice_14 = tensor.extract_slice %arg1[15, 0] [1, 16] [1, 1] : tensor<16x16xi32> to tensor<16xi32>
    %44 = tensor_ext.rotate %extracted_slice_14, %c4 : tensor<16xi32>, index
    %45 = arith.muli %44, %7 : tensor<16xi32>
    %46 = arith.addi %43, %45 : tensor<16xi32>
    %47 = tensor_ext.rotate %46, %c12 : tensor<16xi32>, index
    %48 = arith.addi %35, %47 : tensor<16xi32>
    return %48 : tensor<16xi32>
  }
}

-implement-shift-network

Implement tensor_ext.convert_layout ops as shift newtorks

This pass converts tensor_ext.remap ops into a network of tensor_ext.rotate ops, aiming to minimize the overall latency of the permutation. The input IR must have tensors that correspond to plaintexts or ciphertexts, and be in “ciphertext semantics,” i.e., after an IR has been processed via convert-to-ciphertext-semantics.

The method uses graph coloring, an approach based on Vos-Vos-Erkin 2022, “Efficient Circuits for Permuting and Mapping Packed Values Across Leveled Homomorphic Ciphertexts”.

Example

Command: heir-opt --implement-shift-network tests/Dialect/TensorExt/Transforms/implement_shift_network_example.mlir

Input:

#map = dense<[
  [0, 0, 0, 13],
  [0, 1, 0, 8],
  [0, 2, 0, 4],
  [0, 3, 0, 0],
  [0, 4, 0, 11],
  [0, 5, 0, 7],
  [0, 6, 0, 14],
  [0, 7, 0, 5],
  [0, 8, 0, 15],
  [0, 9, 0, 3],
  [0, 10, 0, 12],
  [0, 11, 0, 6],
  [0, 12, 0, 10],
  [0, 13, 0, 2],
  [0, 14, 0, 9],
  [0, 15, 0, 1]]> : tensor<16x4xi64>
func.func @figure3(%0: tensor<1x16xi32>) -> tensor<1x16xi32> {
  %1 = tensor_ext.remap %0 {permutation = #map} : tensor<1x16xi32>
  return %1 : tensor<1x16xi32>
}

Output:

module {
  func.func @figure3(%arg0: tensor<1x16xi32>) -> tensor<1x16xi32> {
    %extracted_slice = tensor.extract_slice %arg0[0, 0] [1, 16] [1, 1] : tensor<1x16xi32> to tensor<16xi32>
    %cst = arith.constant dense<[1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0]> : tensor<16xi32>
    %0 = arith.muli %extracted_slice, %cst : tensor<16xi32>
    %c1 = arith.constant 1 : index
    %1 = tensor_ext.rotate %0, %c1 : tensor<16xi32>, index
    %cst_0 = arith.constant dense<[1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0]> : tensor<16xi32>
    %2 = arith.muli %1, %cst_0 : tensor<16xi32>
    %cst_1 = arith.constant dense<[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]> : tensor<16xi32>
    %3 = arith.muli %1, %cst_1 : tensor<16xi32>
    %c2 = arith.constant 2 : index
    %4 = tensor_ext.rotate %3, %c2 : tensor<16xi32>, index
    %5 = arith.addi %2, %4 : tensor<16xi32>
    %cst_2 = arith.constant dense<[1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0]> : tensor<16xi32>
    %6 = arith.muli %5, %cst_2 : tensor<16xi32>
    %cst_3 = arith.constant dense<[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]> : tensor<16xi32>
    %7 = arith.muli %5, %cst_3 : tensor<16xi32>
    %c4 = arith.constant 4 : index
    %8 = tensor_ext.rotate %7, %c4 : tensor<16xi32>, index
    %9 = arith.addi %6, %8 : tensor<16xi32>
    %cst_4 = arith.constant dense<[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0]> : tensor<16xi32>
    %10 = arith.muli %9, %cst_4 : tensor<16xi32>
    %cst_5 = arith.constant dense<[1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0]> : tensor<16xi32>
    %11 = arith.muli %9, %cst_5 : tensor<16xi32>
    %c8 = arith.constant 8 : index
    %12 = tensor_ext.rotate %11, %c8 : tensor<16xi32>, index
    %13 = arith.addi %10, %12 : tensor<16xi32>
    %cst_6 = arith.constant dense<[0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0]> : tensor<16xi32>
    %14 = arith.muli %extracted_slice, %cst_6 : tensor<16xi32>
    %cst_7 = arith.constant dense<[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0]> : tensor<16xi32>
    %15 = arith.muli %extracted_slice, %cst_7 : tensor<16xi32>
    %c1_8 = arith.constant 1 : index
    %16 = tensor_ext.rotate %15, %c1_8 : tensor<16xi32>, index
    %17 = arith.addi %14, %16 : tensor<16xi32>
    %cst_9 = arith.constant dense<[0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0]> : tensor<16xi32>
    %18 = arith.muli %17, %cst_9 : tensor<16xi32>
    %cst_10 = arith.constant dense<[0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0]> : tensor<16xi32>
    %19 = arith.muli %17, %cst_10 : tensor<16xi32>
    %c2_11 = arith.constant 2 : index
    %20 = tensor_ext.rotate %19, %c2_11 : tensor<16xi32>, index
    %21 = arith.addi %18, %20 : tensor<16xi32>
    %cst_12 = arith.constant dense<[0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0]> : tensor<16xi32>
    %22 = arith.muli %21, %cst_12 : tensor<16xi32>
    %cst_13 = arith.constant dense<[1, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0]> : tensor<16xi32>
    %23 = arith.muli %21, %cst_13 : tensor<16xi32>
    %c4_14 = arith.constant 4 : index
    %24 = tensor_ext.rotate %23, %c4_14 : tensor<16xi32>, index
    %25 = arith.addi %22, %24 : tensor<16xi32>
    %cst_15 = arith.constant dense<[0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0]> : tensor<16xi32>
    %26 = arith.muli %25, %cst_15 : tensor<16xi32>
    %cst_16 = arith.constant dense<[0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1]> : tensor<16xi32>
    %27 = arith.muli %25, %cst_16 : tensor<16xi32>
    %c8_17 = arith.constant 8 : index
    %28 = tensor_ext.rotate %27, %c8_17 : tensor<16xi32>, index
    %29 = arith.addi %26, %28 : tensor<16xi32>
    %30 = arith.addi %13, %29 : tensor<16xi32>
    %cst_18 = arith.constant dense<[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]> : tensor<16xi32>
    %31 = arith.muli %extracted_slice, %cst_18 : tensor<16xi32>
    %cst_19 = arith.constant dense<[0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]> : tensor<16xi32>
    %32 = arith.muli %extracted_slice, %cst_19 : tensor<16xi32>
    %c1_20 = arith.constant 1 : index
    %33 = tensor_ext.rotate %32, %c1_20 : tensor<16xi32>, index
    %34 = arith.addi %31, %33 : tensor<16xi32>
    %cst_21 = arith.constant dense<[0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]> : tensor<16xi32>
    %35 = arith.muli %34, %cst_21 : tensor<16xi32>
    %c2_22 = arith.constant 2 : index
    %36 = tensor_ext.rotate %35, %c2_22 : tensor<16xi32>, index
    %cst_23 = arith.constant dense<[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0]> : tensor<16xi32>
    %37 = arith.muli %36, %cst_23 : tensor<16xi32>
    %cst_24 = arith.constant dense<[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0]> : tensor<16xi32>
    %38 = arith.muli %36, %cst_24 : tensor<16xi32>
    %c4_25 = arith.constant 4 : index
    %39 = tensor_ext.rotate %38, %c4_25 : tensor<16xi32>, index
    %40 = arith.addi %37, %39 : tensor<16xi32>
    %cst_26 = arith.constant dense<[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]> : tensor<16xi32>
    %41 = arith.muli %40, %cst_26 : tensor<16xi32>
    %cst_27 = arith.constant dense<[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0]> : tensor<16xi32>
    %42 = arith.muli %40, %cst_27 : tensor<16xi32>
    %c8_28 = arith.constant 8 : index
    %43 = tensor_ext.rotate %42, %c8_28 : tensor<16xi32>, index
    %44 = arith.addi %41, %43 : tensor<16xi32>
    %45 = arith.addi %30, %44 : tensor<16xi32>
    %46 = tensor.empty() : tensor<1x16xi32>
    %inserted_slice = tensor.insert_slice %45 into %46[0, 0] [1, 16] [1, 1] : tensor<16xi32> into tensor<1x16xi32>
    return %inserted_slice : tensor<1x16xi32>
  }
}

-inline-activations

Inline activation functions

This pass inlines activation functions into the IR.

Conversion paths from PyTorch to linalg use PyTorch/XLA utilities that convert the torch activation functions into separate functions. This pass inlines these functions into the IR. The candidate activations are identified with an allowlist of function names and are otherwise not checked for correctness. See https://docs.pytorch.org/docs/stable/nn.html#non-linear-activations-weighted-sum-nonlinearity.

Example

Command: heir-opt --inline-activations tests/Transforms/inline_activations/relu.mlir

Input:

module {
  func.func @main(%arg0: tensor<1x512xf32>) -> (tensor<1x512xf32>) {
    %0 = call @relu(%arg0) : (tensor<1x512xf32>) -> tensor<1x512xf32>
    return %0 : tensor<1x512xf32>
  }
  func.func private @relu(%arg0: tensor<1x512xf32>) -> tensor<1x512xf32> {
    %cst = arith.constant dense<0.000000e+00> : tensor<f32>
    %0 = tensor.empty() : tensor<1x512xf32>
    %broadcasted = linalg.broadcast ins(%cst : tensor<f32>) outs(%0 : tensor<1x512xf32>) dimensions = [0, 1]
    %1 = tensor.empty() : tensor<1x512xf32>
    %mapped = linalg.map { arith.maximumf } ins(%arg0, %broadcasted : tensor<1x512xf32>, tensor<1x512xf32>) outs(%1 : tensor<1x512xf32>)
    return %mapped : tensor<1x512xf32>
  }
}

Output:

module {
  func.func @main(%arg0: tensor<1x512xf32>) -> tensor<1x512xf32> {
    %cst = arith.constant dense<0.000000e+00> : tensor<f32>
    %0 = tensor.empty() : tensor<1x512xf32>
    %broadcasted = linalg.broadcast ins(%cst : tensor<f32>) outs(%0 : tensor<1x512xf32>) dimensions = [0, 1] 
    %1 = tensor.empty() : tensor<1x512xf32>
    %mapped = linalg.map { arith.maximumf } ins(%arg0, %broadcasted : tensor<1x512xf32>, tensor<1x512xf32>) outs(%1 : tensor<1x512xf32>)
    return %mapped : tensor<1x512xf32>
  }
}

-insert-rotate

Vectorize arithmetic FHE operations using HECO-style heuristics

This pass implements the SIMD-vectorization passes from the HECO paper.

The pass operates by identifying arithmetic operations that can be suitably combined into a combination of cyclic rotations and vectorized operations on tensors. It further identifies a suitable “slot target” for each operation and heuristically aligns the operations to reduce unnecessary rotations.

This pass by itself does not eliminate any operations, but instead inserts well-chosen rotations so that, for well-structured code (like unrolled affine loops), a subsequent --cse and --canonicalize pass will dramatically reduce the IR. As such, the pass is designed to be paired with the canonicalization patterns in tensor_ext, as well as the collapse-insertion-chains pass, which cleans up remaining insertion and extraction ops after the main simplifications are applied.

Unlike HECO, this pass operates on plaintext types and tensors, along with the HEIR-specific tensor_ext dialect for its cyclic rotate op. It is intended to be run before lowering to a scheme dialect like bgv.

-lattigo-alloc-to-inplace

Convert AllocOps to InplaceOps in Lattigo

This pass converts AllocOps to InplaceOps in Lattigo.

-lattigo-configure-crypto-context

Configure the crypto context in Lattigo

This pass generates helper functions to configure the Lattigo objects for the given function.

For example, for an MLIR function @my_func, the generated helpers have the following signatures

func.func @my_func__configure() -> (!lattigo.bgv.evaluator, !lattigo.bgv.parameter, !lattigo.bgv.encoder, !lattigo.rlwe.encryptor, !lattigo.rlwe.decryptor)

Options

-entry-function : Default entry function name of entry function.

-layout-optimization

Optimize layout conversions in the IR

This pass performance a greedy layout optimization pass similar to the automatic layout assignment from A Tensor Compiler with Automatic Data Packing for Simple and Efficient Fully Homomorphic Encryption. The pass assumes that an initial layout assignment was provided on each operation through the layout-propagation pass.

The pass iterates on each operation of the IR in reverse order, attempting to hoist a layout conversion of the operation’s result before the operation. For each of the result’s layout conversions, the pass will compute the net cost of hoisting the conversion through the operation by considering the following:

  1. The cost of performing the operation with new input layouts that result in the desired layout.
  2. The cost of the converting the layout of each input.
  3. The new cost of converting from the desired layout to each other layout conversions of the result.

The layout conversion that results in the lowest net cost is chosen to be hoisted.

Example

Command: heir-opt --layout-optimization --canonicalize tests/Transforms/layout_optimization/hoist_matvec.mlir

Input:

#vec_layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : (i0 - slot) mod 1024 = 4 and i0 >= 0 and 0 >= i0 and slot >= 0 and 1023 >= slot and ct = 0 }">
#vec_layout_2 = #tensor_ext.layout<"{ [i0] -> [ct, slot] : (i0 - slot) mod 1024 = 7 and i0 >= 0 and 0 >= i0 and slot >= 0 and 1023 >= slot and ct = 0 }">
#mat_layout = #tensor_ext.layout<"{ [row, col] -> [ct, slot] : (slot - row) mod 512 = 0 and (ct + slot - col) mod 512 = 0 and row >= 0 and col >= 0 and ct >= 0 and slot >= 0 and 1023 >= slot and 511 >= ct and 511 >= row and 511 >= col }">


func.func @main(%arg0: tensor<512x512xf32>, %arg1: !secret.secret<tensor<512xf32>> {tensor_ext.layout = #vec_layout}) -> (!secret.secret<tensor<512xf32>> {tensor_ext.layout = #vec_layout_2}) {
  %cst = arith.constant dense<0.000000e+00> : tensor<512xf32>
  %0 = tensor.empty() : tensor<512xf32>
  %1 = tensor_ext.assign_layout %0 {layout = #vec_layout, tensor_ext.layout = #vec_layout} : tensor<512xf32>
  %2 = tensor_ext.assign_layout %arg0 {layout = #mat_layout, tensor_ext.layout = #mat_layout} : tensor<512x512xf32>
  %3 = secret.generic(%arg1: !secret.secret<tensor<512xf32>> {tensor_ext.layout = #vec_layout}) {
  ^body(%input0: tensor<512xf32>):
    %4 = linalg.matvec {tensor_ext.layout = #vec_layout, secret.kernel = #secret.kernel<name="MatvecDiagonal", force=false>}
        ins(%2, %input0 : tensor<512x512xf32>, tensor<512xf32>) outs(%1 : tensor<512xf32>) -> tensor<512xf32>
    %5 = tensor_ext.convert_layout %4 {from_layout = #vec_layout, tensor_ext.layout = #vec_layout_2, to_layout = #vec_layout_2} : tensor<512xf32>
    secret.yield %5 : tensor<512xf32>
  } -> (!secret.secret<tensor<512xf32>> {tensor_ext.layout = #vec_layout_2})
  return %3 : !secret.secret<tensor<512xf32>>
}

Output:

#kernel = #secret.kernel<name = "MatvecDiagonal", force = false>
#layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : (i0 - slot) mod 1024 = 7 and i0 >= 0 and 0 >= i0 and slot >= 0 and 1023 >= slot and ct = 0 }">
#layout1 = #tensor_ext.layout<"{ [i0, i1] -> [ct, slot] : (4 + i0) mod 512 = 0 and (-4 - i1 + ct) mod 512 = 0 and (7 + slot) mod 1024 = 0 and 0 <= i0 <= 511 and 0 <= i1 <= 511 and 0 <= ct <= 511 and 0 <= slot <= 1023 }">
module {
  func.func @main(%arg0: tensor<512x512xf32>, %arg1: !secret.secret<tensor<512xf32>> {tensor_ext.layout = #layout}) -> (!secret.secret<tensor<512xf32>> {tensor_ext.layout = #layout}) {
    %0 = tensor.empty() : tensor<512xf32>
    %1 = tensor_ext.assign_layout %arg0 {layout = #layout1, tensor_ext.layout = #layout1} : tensor<512x512xf32>
    %2 = tensor_ext.assign_layout %0 {layout = #layout, tensor_ext.layout = #layout} : tensor<512xf32>
    %3 = secret.generic(%arg1: !secret.secret<tensor<512xf32>> {tensor_ext.layout = #layout}) {
    ^body(%input0: tensor<512xf32>):
      %4 = linalg.matvec {secret.kernel = #kernel, tensor_ext.layout = #layout} ins(%1, %input0 : tensor<512x512xf32>, tensor<512xf32>) outs(%2 : tensor<512xf32>) -> tensor<512xf32>
      secret.yield %4 : tensor<512xf32>
    } -> (!secret.secret<tensor<512xf32>> {tensor_ext.layout = #layout})
    return %3 : !secret.secret<tensor<512xf32>>
  }
}

Options

-ciphertext-size  : Power of two length of the ciphertexts the data is packed in.
-vve-random-seed  : Random seed for Vos-Vos-Erkin shift network randomization. Will be hash-combined with additional seeds based on layouts being converted from and to.
-vve-random-tries : Number of random tries used to find best Vos-Vos-Erkin shift network during layout optimization.

-layout-propagation

Propagate ciphertext layouts through the IR

This pass performs a forward propagation of layout (packing) information through the input IR, starting from the assumption that each secret tensor argument to a function has a row-major layout.

The chosen layouts (Integer Relations) are annotated on ops throughout the IR. In particular,

  • Ops with a nested region and block arguments use a dictionary attribute to mark the layout of each block argument. func.func in particular uses the tensor_ext.layout dialect attribute, while others use an affine map attribute.
  • Other ops annotate their results with layouts as an ArrayAttr of layouts. The order of the affine maps corresponds to the order of results.

When a plaintext SSA value is encountered as an input to a secret operation, a tensor_ext.assign_layout op is inserted that assigns it a default layout. This semantically corresponds to a plaintext packing operation. This is performed as late as possible before the SSA value is used, to avoid unnecessary layout conversions of plaintexts. This implies that not all SSA values in the IR are annotated with layouts, only those that have secret results or secret operands.

When two incompatible layouts are encountered as operands to the same op, tensor_ext.convert_layout ops are inserted. For example, consider the linalg.reduce operation for a summation. Summing along each of the two axes of a row-major-packed tensor<32x32xi16> results in two tensor<32xi16>, but with incompatible layouts: the first has a compact layout residing in the first 32-entries of a ciphertext, while the second is a strided layout with a stride of 32.

The converted op is arbitrarily chosen to have the layout of the first input, and later passes are responsible for optimizing the choice of which operand is converted and where the conversion operations are placed. This separation of duties allows this pass to be reused as a pure dataflow analysis, in which case it annotates an un-annotated IR with layout attributes.

Example

Command: heir-opt --layout-propagation tests/Transforms/layout_propagation/doctest.mlir

Input:

// An MNIST-like two-layer neural network with cleartext weights and biases
// and a secret input.

func.func @main(
    %arg0: tensor<512x784xf32>,
    %arg1: tensor<512xf32>,
    %arg2: tensor<10x512xf32>,
    %arg3: tensor<10xf32>,
    %arg4: !secret.secret<tensor<784xf32>>) -> !secret.secret<tensor<10xf32>> {
  %cst = arith.constant dense<0.000000e+00> : tensor<512xf32>
  %cst_0 = arith.constant dense<0.000000e+00> : tensor<10xf32>
  %0 = tensor.empty() : tensor<784x512xf32>
  %1 = tensor.empty() : tensor<512x10xf32>
  %2 = secret.generic(%arg4: !secret.secret<tensor<784xf32>>) {
  ^body(%input0: tensor<784xf32>):
    %transposed = linalg.transpose ins(%arg0 : tensor<512x784xf32>) outs(%0 : tensor<784x512xf32>) permutation = [1, 0]
    %3 = linalg.vecmat ins(%input0, %transposed : tensor<784xf32>, tensor<784x512xf32>) outs(%cst : tensor<512xf32>) -> tensor<512xf32>
    %4 = arith.addf %arg1, %3 : tensor<512xf32>
    %5 = arith.maximumf %4, %cst : tensor<512xf32>
    %transposed_1 = linalg.transpose ins(%arg2 : tensor<10x512xf32>) outs(%1 : tensor<512x10xf32>) permutation = [1, 0]
    %6 = linalg.vecmat ins(%5, %transposed_1 : tensor<512xf32>, tensor<512x10xf32>) outs(%cst_0 : tensor<10xf32>) -> tensor<10xf32>
    %7 = arith.addf %arg3, %6 : tensor<10xf32>
    secret.yield %7 : tensor<10xf32>
  } -> !secret.secret<tensor<10xf32>>
  return %2 : !secret.secret<tensor<10xf32>>
}

Output:

#kernel = #secret.kernel<name = "VecmatDiagonal", force = false>
#layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : ct = 0 and (-i0 + slot) mod 16 = 0 and 0 <= i0 <= 9 and 0 <= slot <= 1023 }">
#layout1 = #tensor_ext.layout<"{ [i0] -> [ct, slot] : ct = 0 and (-i0 + slot) mod 1024 = 0 and 0 <= i0 <= 783 and 0 <= slot <= 1023 }">
#layout2 = #tensor_ext.layout<"{ [i0, i1] -> [ct, slot] : (i0 - i1 + ct) mod 512 = 0 and (-i1 + ct + slot) mod 1024 = 0 and 0 <= i0 <= 511 and 0 <= i1 <= 783 and 0 <= ct <= 511 and 0 <= slot <= 1023 }">
#layout3 = #tensor_ext.layout<"{ [i0] -> [ct, slot] : ct = 0 and (-i0 + slot) mod 512 = 0 and 0 <= i0 <= 511 and 0 <= slot <= 1023 }">
#layout4 = #tensor_ext.layout<"{ [i0, i1] -> [ct, slot] : (i0 - i1 + ct) mod 16 = 0 and (-i1 + ct + slot) mod 512 = 0 and 0 <= i0 <= 9 and 0 <= i1 <= 511 and 0 <= ct <= 15 and 0 <= slot <= 1023 }">
module {
  func.func @main(%arg0: tensor<512x784xf32>, %arg1: tensor<512xf32>, %arg2: tensor<10x512xf32>, %arg3: tensor<10xf32>, %arg4: !secret.secret<tensor<784xf32>> {tensor_ext.layout = #layout1}) -> (!secret.secret<tensor<10xf32>> {tensor_ext.layout = #layout}) {
    %cst = arith.constant dense<0.000000e+00> : tensor<512xf32>
    %cst_0 = arith.constant dense<0.000000e+00> : tensor<10xf32>
    %0 = tensor.empty() : tensor<784x512xf32>
    %1 = tensor.empty() : tensor<512x10xf32>
    %2 = secret.generic(%arg4: !secret.secret<tensor<784xf32>> {tensor_ext.layout = #layout1}) {
    ^body(%input0: tensor<784xf32>):
      %transposed = linalg.transpose ins(%arg0 : tensor<512x784xf32>) outs(%0 : tensor<784x512xf32>) permutation = [1, 0] 
      %3 = tensor_ext.assign_layout %transposed {layout = #layout2, tensor_ext.layout = #layout2} : tensor<784x512xf32>
      %4 = tensor_ext.assign_layout %cst {layout = #layout3, tensor_ext.layout = #layout3} : tensor<512xf32>
      %5 = linalg.vecmat {secret.kernel = #kernel, tensor_ext.layout = #layout3} ins(%input0, %3 : tensor<784xf32>, tensor<784x512xf32>) outs(%4 : tensor<512xf32>) -> tensor<512xf32>
      %6 = tensor_ext.assign_layout %arg1 {layout = #layout3, tensor_ext.layout = #layout3} : tensor<512xf32>
      %7 = arith.addf %6, %5 {tensor_ext.layout = #layout3} : tensor<512xf32>
      %8 = tensor_ext.assign_layout %cst {layout = #layout3, tensor_ext.layout = #layout3} : tensor<512xf32>
      %9 = arith.maximumf %7, %8 {tensor_ext.layout = #layout3} : tensor<512xf32>
      %transposed_1 = linalg.transpose ins(%arg2 : tensor<10x512xf32>) outs(%1 : tensor<512x10xf32>) permutation = [1, 0] 
      %10 = tensor_ext.assign_layout %transposed_1 {layout = #layout4, tensor_ext.layout = #layout4} : tensor<512x10xf32>
      %11 = tensor_ext.assign_layout %cst_0 {layout = #layout, tensor_ext.layout = #layout} : tensor<10xf32>
      %12 = linalg.vecmat {secret.kernel = #kernel, tensor_ext.layout = #layout} ins(%9, %10 : tensor<512xf32>, tensor<512x10xf32>) outs(%11 : tensor<10xf32>) -> tensor<10xf32>
      %13 = tensor_ext.assign_layout %arg3 {layout = #layout, tensor_ext.layout = #layout} : tensor<10xf32>
      %14 = arith.addf %13, %12 {tensor_ext.layout = #layout} : tensor<10xf32>
      secret.yield %14 : tensor<10xf32>
    } -> (!secret.secret<tensor<10xf32>> {tensor_ext.layout = #layout})
    return %2 : !secret.secret<tensor<10xf32>>
  }
}

Options

-ciphertext-size : Power of two length of the ciphertexts the data is packed in.

-linalg-canonicalizations

This pass canonicalizes the linalg.transpose operation of a constant into a transposed constant.

This pass canonicalizes the linalg.transpose operation of a constant into a transposed constant.

-lower-polynomial-eval

Lowers the polynomial.eval operation

This pass lowers the polynomial.eval operation to a sequence of arithmetic operations in the relevant dialect.

Dialects that wish to support this pass must implement the DialectPolynomialEvalInterface dialect interface, which informs this pass what operations in the target dialect correspond to scalar multiplication and addition, as well as how to properly materialize constants as values.

This pass supports multiple options for lowering a polynomial.eval op, including the following. The required basis representation of the polynomial is listed alongside each method. The chosen method is controlled by the method pass option, which defaults to automatically select the method.

  • "horner": Horner’s method (monomial basis)
  • "ps" Paterson-Stockmeyer (monomial basis)
  • "pscheb": Paterson-Stockmeyer (Chebyshev basis)

// TODO(#1565): Add support for Chebyshev-basis methods // - "clenshaw": Clenshaw’s method (Chebyshev basis) // - "bsgs": Baby Step Giant Step (Chebyshev basis)

Options

-method : The method used to lower polynomial.eval

-lower-unpack

Lower tensor_ext.unpack to standard MLIR

This pass lowers tensor_ext.unpack.

-lwe-add-debug-port

Add debug port to (R)LWE encrypted functions

This pass adds debug ports to the specified function in the IR. The debug ports are prefixed with “__heir_debug” and are invoked after each homomorphic operation in the function. The debug ports are declarations and user should provide functions with the same name in their code.

For example, if the function is called “foo”, the secret key is added to its arguments, and the debug port is called after each homomorphic operation:

// declaration of external debug function
func.func private @__heir_debug(%sk : !sk, %ct : !ct)

// secret key added as function arg
func.func @foo(%sk : !sk, ...) {
  %ct = lwe.radd ...
  // invoke external debug function
  __heir_debug(%sk, %ct)
  %ct1 = lwe.rmul ...
  __heir_debug(%sk, %ct1)
  ...
}

Options

-entry-function : Default entry function name of entry function.

-lwe-to-lattigo

Lower lwe to lattigo dialect.

This pass lowers the lwe dialect to Lattigo dialect.

-lwe-to-openfhe

Lower lwe to openfhe dialect.

This pass lowers the lwe dialect to Openfhe dialect. Currently, this also includes patterns that apply directly to ckks and bgv dialect operations. TODO (#1193): investigate if the need for ckks/bgv patterns in --lwe-to-openfhe is permanent.

-lwe-to-polynomial

Lower lwe to polynomial dialect.

This pass lowers the lwe dialect to polynomial dialect.

-memref-global-replace

MemrefGlobalReplacePass forwards global memrefs accessors to arithmetic values

This pass forwards constant global MemRef values to referencing affine loads. This pass requires that the MemRef global values are initialized as constants and that the affine load access indices are constants (i.e. not variadic). Unroll affine loops prior to running this pass.

MemRef removal is required to remove any memory allocations from the input model (for example, TensorFlow models contain global memory holding model weights) to support FHE transpilation.

Example

Command: heir-opt --memref-global-replace tests/Transforms/memref_global_replace/doctest.mlir

Input:

module {
  memref.global "private" constant @__constant_8xi16 : memref<2x4xi16> = dense<[[-10, 20, 3, 4], [5, 6, 7, 8]]>
  func.func @main() -> i16 {
    %c1 = arith.constant 1 : index
    %c2 = arith.constant 2 : index
    %0 = memref.get_global @__constant_8xi16 : memref<2x4xi16>
    %1 = affine.load %0[%c1, %c1 + %c2] : memref<2x4xi16>
    return %1 : i16
  }
}

Output:

module {
  func.func @main() -> i16 {
    %c1 = arith.constant 1 : index
    %c2 = arith.constant 2 : index
    %c8_i16 = arith.constant 8 : i16
    return %c8_i16 : i16
  }
}

-mod-arith-to-arith

Lower mod_arith to standard arith.

This pass lowers the mod_arith dialect to their arith equivalents.

-mod-arith-to-mac

Finds consecutive ModArith mul and add operations and converts them to a Mac operation

Walks over the programs to find Add operations, it checks if the any operands originates from a mul operation. If so, it converts the Add operation to a Mac operation and removes the mul operation.

-openfhe-configure-crypto-context

Configure the crypto context in OpenFHE

This pass generates helper functions to generate and configure the OpenFHE crypto context for the given function. Generating the crypto context sets the appropriate encryption parameters, while the configuration generates the necessary evaluation keys (relinearization and rotation keys).

For the options, reader can refer to the OpenFHE documentation at https://github.com/openfheorg/openfhe-development/blob/main/src/pke/examples/README.md#description-of-the-cryptocontext-parameters-and-their-restrictions

For example, for an MLIR function @my_func, the generated helpers have the following signatures

func.func  @my_func__generate_crypto_context() -> !openfhe.crypto_context

func.func  @my_func__configure_crypto_context(!openfhe.crypto_context, !openfhe.private_key) -> !openfhe.crypto_context

Options

-entry-function                 : Default entry function name of entry function.
-mul-depth                      : Manually specify the mul depth
-ring-dim                       : Manually specify the ring dimension (insecure is implied)
-batch-size                     : Manually specify the batch size
-first-mod-size                 : Manually specify the first mod size
-scaling-mod-size               : Manually specify the scaling mod size
-digit-size                     : Manually specify the digit size for relinearization
-num-large-digits               : Manually specify the number of large digits for HYBRID relinearization
-max-relin-sk-deg               : Manually specify the max number of relin sk deg
-insecure                       : Whether to use insecure parameter (defaults to false)
-key-switching-technique-bv     : Whether to use BV key switching technique (defaults to false)
-scaling-technique-fixed-manual : Whether to use fixed manual scaling technique (defaults to false)
-level-budget-encode            : Level budget for CKKS bootstrap encode (s2c) phase
-level-budget-decode            : Level budget for CKKS bootstrap decode (c2s) phase

-openfhe-count-add-and-key-switch

Count the number of add and key-switch operations in OpenFHE

This pass counts the number of add and key-switch operations in the given function.

This is used for setting the EvalAddCount and EvalKeySwitchCount in OpenFHE library. Cf. Alexandru et al. 2024 for why this is important for security.

The detailed definition of these counts could be found in the KPZ21 paper Revisiting Homomorphic Encryption Schemes for Finite Fields

The pass should be run at the secret arithmetic level when management operations have been inserted and the IR is stable.

-openfhe-fast-rotation-precompute

Identify and apply EvalFastRotation when possible.

This pass identifies when a ciphertext is rotated by multiple different shifts, and replaces the EvalRot ops with EvalFastRotationPrecompute followed by EvalFastRotate.

-operation-balancer

This pass balances addition and multiplication operations.

This pass examines a tree or graph of add and multiplication operations and balances them to minimize the depth of the tree. This exposes better parallelization and reducing the multiplication depth can decrease the parameters used in FHE, which improves performance. This pass is not necessarily optimal, as there may be intermediate computations that this pass does not optimally minimize the depth for.

The algorithm is to analyze a graph of addition operations and do a depth-first search for the operands (from the last computed values in the graph). If there are intermediate computations that are used more than once, then the pass treats that computation as its own tree to balance instead of trying to minimize the global depth of the tree.

This pass only runs on addition and multiplication operations on the arithmetic dialect that are encapsulated inside a secret.generic.

This pass was inspired by section 2.6 of ‘EVA Improved: Compiler and Extension Library for CKKS’ by Chowdhary et al.

-optimize-relinearization

Optimize placement of relinearization ops

This pass defers relinearization ops as late as possible in the IR. This is more efficient in cases where multiplication operations are followed by additions, such as in a dot product. Because relinearization also adds error, deferring it can reduce the need for bootstrapping.

In this pass, we use an integer linear program to determine the optimal relinearization strategy. It solves an ILP for each func op in the IR.

The assumptions of this pass include:

  • All return values of functions must be linearized.
  • All ciphertext arguments to an op must have the same key basis
  • Rotation op inputs must have be linearized.

For an ILP model specification, see the docs at the HEIR website. The model is an adaptation of the ILP described in a blog post by Jeremy Kun.

Options

-use-loc-based-variable-names : When true, the ILP uses op source locations in variable names, which can help debug ILP model bugs.
-allow-mixed-degree-operands  : When true, allow ops to have mixed-degree ciphertexts as inputs, e.g., adding two ciphertexts with different key bases; this is supported by many FHE backends, like OpenFHE and Lattigo

-polynomial-approximation

Approximate ops by polynomials

This pass replaces certain operations that are incompatible with the FHE computational model with polynomial approximations.

The pass applies to the following ops in the math dialect. When the op is binary, the pass applies when one op is the result of an arith.constant which is scalar-valued or a splatted tensor.

  • absf
  • acos
  • acosh
  • asin
  • asinh
  • atan2
  • atan
  • atanh
  • cbrt
  • ceil
  • copysign
  • cos
  • cosh
  • erf
  • erfc
  • exp2
  • exp
  • expm1
  • floor
  • fpowi
  • log10
  • log1p
  • log2
  • log
  • powf
  • round
  • roundeven
  • rsqrt
  • sin
  • sinh
  • sqrt
  • tan
  • tanh
  • trunc

As well as the following ops in the math_ext dialect:

  • sign

The following ops in the arith dialect are also supported:

  • maxf
  • maxnumf
  • minf
  • minnumf

These ops are replaced with polynomial.eval ops with a static polynomial attribute.

Example

Command: heir-opt --polynomial-approximation tests/Transforms/polynomial_approximation/doctest.mlir

Input:

func.func @test_exp(%x: f32) -> f32 {
  %0 = math.exp %x {
      degree = 3 : i32,
      domain_lower = -1.0 : f64,
      domain_upper = 1.0 : f64} : f32
  return %0 : f32
}

Output:

#ring_f64 = #polynomial.ring<coefficientType = f64>
!poly = !polynomial.polynomial<ring = #ring_f64>
module {
  func.func @test_exp(%arg0: f32) -> f32 {
    %0 = polynomial.eval #polynomial<typed_chebyshev_polynomial <[1.2660658705156256, 1.1303178227397606, 0.2714863941909304, 0.044883370904043471]> : !poly>, %arg0 {domain_lower = -1.000000e+00 : f64, domain_upper = 1.000000e+00 : f64} : f32
    return %0 : f32
  }
}

-polynomial-to-mod-arith

Lower polynomial to standard MLIR dialects.

This pass lowers the polynomial dialect to standard MLIR plus mod_arith, including possibly ops from affine, tensor, linalg, and arith.

Options

-build-materializations : Whether to build materializations

-populate-scale-bgv

Populate the scale for BGV (GHS variant) ciphertext

In the original BGV scheme, it is required that each modulus in the modulus chain is a prime number q such that $q \equiv 1 \pmod{t}$, the plaintext modulus. This is to ensure that the after each modulus switching, the plaintext message is preserved. However, this limits the possible choices of the moduli chain.

In the GHS variant of BGV, such requirement is removed by introducing scaling factor to the ciphertext, with the cost of scale management. This pass is responsible for such management.

This pass relies on concrete SchemeParamAttr annotated on the module to determine the scale for each ciphertext. Such annotation can be generated by the generate-param-bgv pass.

Example

Command: heir-opt tests/Transforms/populate_scale/bgv/doctest.mlir --populate-scale-bgv

Input:

module attributes {bgv.schemeParam = #bgv.scheme_param<logN = 13, Q = [67239937, 8796093202433], P = [8796093349889], plaintextModulus = 65537>, scheme.bgv} {
  func.func @mul(%arg0: !secret.secret<i16>) -> !secret.secret<i16> {
    %0 = secret.generic(%arg0 : !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}) {
    ^body(%input0: i16):
      %1 = arith.muli %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 1, dimension = 3>} : i16
      %2 = mgmt.relinearize %1 {mgmt.mgmt = #mgmt.mgmt<level = 1>} : i16
      %3 = mgmt.modreduce %2 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : i16
      secret.yield %3 : i16
    } -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<i16>
  }
}

Output:

module attributes {bgv.schemeParam = #bgv.scheme_param<logN = 13, Q = [67239937, 8796093202433], P = [8796093349889], plaintextModulus = 65537>, scheme.bgv} {
  func.func @mul(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1, scale = 1>}) -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0, scale = 42541>}) {
    %0 = secret.generic(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1, scale = 1>}) {
    ^body(%input0: i16):
      %1 = arith.muli %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 1, dimension = 3, scale = 1>} : i16
      %2 = mgmt.relinearize %1 {mgmt.mgmt = #mgmt.mgmt<level = 1, scale = 1>} : i16
      %3 = mgmt.modreduce %2 {mgmt.mgmt = #mgmt.mgmt<level = 0, scale = 42541>} : i16
      secret.yield %3 : i16
    } -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0, scale = 42541>})
    return %0 : !secret.secret<i16>
  }
}

-populate-scale-ckks

Populate the scale for CKKS ciphertext

In CKKS, each ciphertext is associated with a scaling factor $\Delta$, and such scaling factor will change after homomorphic operations such as multiplication and modulus reducing.

However, certain operations such as addition require the input ciphertexts to have the same scale. This pass is then responsible for managing the scale of the ciphertexts.

This pass relies on concrete SchemeParamAttr annotated on the module to determine the scale for each ciphertext. Such annotation can be generated by the generate-param-ckks pass.

The scaling factor is expressed in logarithm form.

Example

Command: heir-opt tests/Transforms/populate_scale/ckks/doctest.mlir --populate-scale-ckks

Input:

module attributes {ckks.schemeParam = #ckks.scheme_param<logN = 13, Q = [36028797019389953, 35184372121601], P = [36028797019488257], logDefaultScale = 45>, scheme.ckks} {
  func.func @mul(%arg0: !secret.secret<f32>) -> !secret.secret<f32> {
    %0 = secret.generic(%arg0 : !secret.secret<f32> {mgmt.mgmt = #mgmt.mgmt<level = 1, scale = 45>}) {
    ^body(%input0: f32):
      %1 = arith.mulf %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 1, dimension = 3, scale = 90>} : f32
      %2 = mgmt.relinearize %1 {mgmt.mgmt = #mgmt.mgmt<level = 1>} : f32
      %3 = mgmt.modreduce %2 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : f32
      secret.yield %3 : f32
    } -> (!secret.secret<f32> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<f32>
  }
}

Output:

module attributes {ckks.schemeParam = #ckks.scheme_param<logN = 13, Q = [36028797019389953, 35184372121601], P = [36028797019488257], logDefaultScale = 45>, scheme.ckks} {
  func.func @mul(%arg0: !secret.secret<f32> {mgmt.mgmt = #mgmt.mgmt<level = 1, scale = 45>}) -> (!secret.secret<f32> {mgmt.mgmt = #mgmt.mgmt<level = 0, scale = 45>}) {
    %0 = secret.generic(%arg0: !secret.secret<f32> {mgmt.mgmt = #mgmt.mgmt<level = 1, scale = 45>}) {
    ^body(%input0: f32):
      %1 = arith.mulf %input0, %input0 {mgmt.mgmt = #mgmt.mgmt<level = 1, dimension = 3, scale = 90>} : f32
      %2 = mgmt.relinearize %1 {mgmt.mgmt = #mgmt.mgmt<level = 1, scale = 90>} : f32
      %3 = mgmt.modreduce %2 {mgmt.mgmt = #mgmt.mgmt<level = 0, scale = 45>} : f32
      secret.yield %3 : f32
    } -> (!secret.secret<f32> {mgmt.mgmt = #mgmt.mgmt<level = 0, scale = 45>})
    return %0 : !secret.secret<f32>
  }
}

Options

-before-mul-include-first-mul : Modulus switching before each multiplication, including the first multiplication (default to false)

-propagate-annotation

Propagate annotation from operation to subsequent operations

This pass propagates the attribute from one operation to subsequent operations if these operations does not have the attribute already.

Example: with --propagate-annotation=attr-name=test.attr

func.func @foo(%arg0: i16 {test.attr = 1}) -> i16 {
  %0 = arith.muli %arg0, %arg0 : i16
  %1 = mgmt.relinearize %0 : i16
  return %1 : i16
}

the above IR becomes

func.func @foo(%arg0: i16 {test.attr = 1 : i64}) -> i16 {
  %0 = arith.muli %arg0, %arg0 {test.attr = 1 : i64} : i16
  %1 = mgmt.relinearize %0 {test.attr = 1 : i64} : i16
  return {test.attr = 1 : i64} %1 : i16
}

Options

-attr-name : The attribute name to propagate with.
-reverse   : Whether to propagate in reverse

-relu-canonicalizations

Rewrites comparison and selection to a min/max

This pass rewrites selections with a constant comparison to a min/max operation.

Example

Command: heir-opt --relu-canonicalizations --canonicalize tests/Transforms/relu_canonicalizations/doctest.mlir

Input:

func.func @relu(%arg0: f32) -> f32 {
  %cst_0 = arith.constant 0.000000e+00 : f32
  %0 = arith.cmpf ugt, %arg0, %cst_0 : f32
  %1 = arith.select %0, %arg0, %cst_0 : f32
  return %1 : f32
}

Output:

module {
  func.func @relu(%arg0: f32) -> f32 {
    %cst = arith.constant 0.000000e+00 : f32
    %0 = arith.maximumf %arg0, %cst : f32
    return %0 : f32
  }
}

-remove-unused-memref

Cleanup any unused memrefs

Scan the IR for unused memrefs and remove them.

This pass looks for locally allocated memrefs that are never used and deletes them. This pass can be used as a cleanup pass from other IR simplifications that forward stores to loads.

-rotate-and-reduce

Use a logarithmic number of rotations to reduce a tensor.

This pass identifies when a commutative, associative binary operation is used to reduce all of the entries of a tensor to a single value, and optimizes the operations by using a logarithmic number of reduction operations.

In particular, this pass identifies an unrolled set of operations of the form (the binary ops may come in any order):

%0 = tensor.extract %t[0] : tensor<8xi32>
%1 = tensor.extract %t[1] : tensor<8xi32>
%2 = tensor.extract %t[2] : tensor<8xi32>
%3 = tensor.extract %t[3] : tensor<8xi32>
%4 = tensor.extract %t[4] : tensor<8xi32>
%5 = tensor.extract %t[5] : tensor<8xi32>
%6 = tensor.extract %t[6] : tensor<8xi32>
%7 = tensor.extract %t[7] : tensor<8xi32>
%8 = arith.addi %0, %1 : i32
%9 = arith.addi %8, %2 : i32
%10 = arith.addi %9, %3 : i32
%11 = arith.addi %10, %4 : i32
%12 = arith.addi %11, %5 : i32
%13 = arith.addi %12, %6 : i32
%14 = arith.addi %13, %7 : i32

and replaces it with a logarithmic number of rotate and addi operations:

%0 = tensor_ext.rotate %t, 4 : tensor<8xi32>
%1 = arith.addi %t, %0 : tensor<8xi32>
%2 = tensor_ext.rotate %1, 2 : tensor<8xi32>
%3 = arith.addi %1, %2 : tensor<8xi32>
%4 = tensor_ext.rotate %3, 1 : tensor<8xi32>
%5 = arith.addi %3, %4 : tensor<8xi32>

-secret-add-debug-port

Add debug port to secret-arithmetic ops

This pass adds debug ports to secret-arithmetic ops in the IR, namely operations wrapped by secret.generic. The debug ports are prefixed with “__heir_debug” and are invoked after each operation in the generic body. The debug ports are declarations and user should provide functions with the same name in their code.

For example, if the function is called “foo”, the debug port is called after each homomorphic operation:

// declaration of external debug function
func.func private @__heir_debug_tensor_8xi16_(tensor<8xi16>)

func.func @foo(...) {
  secret.generic {
    %0 = arith.addi ...
    // invoke external debug function
    __heir_debug_tensor_8xi16_(%0)
    %1 = arith.muli ...
    __heir_debug_tensor_8xi16_(%1)
  }
}

-secret-capture-generic-ambient-scope

Capture the ambient scope used in a secret.generic

For each value used in the body of a secret.generic op, which is defined in the ambient scope outside the generic, add it to the argument list of the generic.

-secret-distribute-generic

Distribute generic ops through their bodies.

Converts generic ops whose region contains many ops into smaller sequences of generic ops whose regions contain a single op, dropping the generic part from any resulting generic ops that have no secret.secret inputs. If the op has associated regions, and the operands are not secret, then the generic is distributed recursively through the op’s regions as well.

This pass is intended to be used as part of a front-end pipeline, where a program that operates on a secret type annotates the input to a region as secret, and then wraps the contents of the region in a single large secret.generic, then uses this pass to simplify it.

The distribute-through option allows one to specify a comma-separated list of op names (e.g., distribute-thorugh="affine.for,scf.if"), which limits the distribution to only pass through those ops. If unset, all ops are distributed through when possible.

Options

-distribute-through : comma-separated list of ops that should be distributed through

-secret-extract-generic-body

Extract the bodies of all generic ops into functions

This pass extracts the body of all generic ops into functions, and replaces the generic bodies with call ops. Used as a sub-operation in some passes, and extracted into its own pass for testing purposes.

This pass works best when --secret-generic-absorb-constants is run before it so that the extracted function contains any constants used in the generic op’s body.

-secret-forget-secrets

Convert secret types to standard types

Drop the secret<...> type from the IR, replacing it with the contained type and the corresponding cleartext computation.

secret.cast ops are replaced with freshly alloc’ed memrefs that extract individual bits of the input type or reshape them if possible.

-secret-generic-absorb-constants

Copy constants into a secret.generic body

For each constant value used in the body of a secret.generic op, which is defined in the ambient scope outside the generic, add it’s definition into the generic body.

-secret-generic-absorb-dealloc

Copy deallocs of internal memrefs into a secret.generic body

For each memref allocated and used only within a body of a secret.generic op, add it’s dealloc of the memref into its generic body.

-secret-import-execution-result

Annotate execution result to secret-arithmetic ops

When the execution result of each op is known by secret-add-debug-port pass, the result could be imported back to the IR.

This pass adds a new attribute secret.execution_result to the secret-arithmetic ops.

This is useful when users want to compare the precision of the result between the plaintext and the ciphertext (especially the CKKS case).

For example, if you have a trace.log that is generated by plaintext backend with --secret-add-debug-port where the result is printed out like

1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0
2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0

Each line corresponds to one SSA value in the IR. You can then import the result back to the IR by using --secret-import-execution-result=file-name=trace.log.

func.func @foo(...) {
  secret.generic {
    %0 = arith.addi ... {secret.execution_result = [1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0]}
    %1 = arith.muli ... {secret.execution_result = [2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0]}
  }
}

Options

-file-name : file name of the execution result

-secret-insert-mgmt-bfv

Place BFV ciphertext management operations

This pass inserts relinearization operation for multiplication, and compute the multiplicative depth, or the level information.

For most cases B/FV is instantiated with no mod reduce so it is not a leveled scheme. However, for instantiating B/FV parameters it is often meaningful to know the multiplicative depth of the circuit.

Example

Command: heir-opt --secret-insert-mgmt-bfv tests/Transforms/secret_insert_mgmt_bfv/doctest.mlir

Input:

func.func @func(%arg0: !secret.secret<i16>, %arg1: !secret.secret<i16>) -> !secret.secret<i16> {
  %0 = secret.generic(%arg0: !secret.secret<i16>, %arg1: !secret.secret<i16>) {
  ^bb0(%arg2: i16, %arg3: i16):
    %1 = arith.muli %arg2, %arg3 : i16
    %2 = arith.addi %1, %arg3 : i16
    secret.yield %2 : i16
  } -> !secret.secret<i16>
  return %0 : !secret.secret<i16>
}

Output:

module attributes {scheme.bfv} {
  func.func @func(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}, %arg1: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}) -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}) {
    %0 = secret.generic(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}, %arg1: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}) {
    ^body(%input0: i16, %input1: i16):
      %1 = arith.muli %input0, %input1 {mgmt.mgmt = #mgmt.mgmt<level = 1, dimension = 3>} : i16
      %2 = mgmt.relinearize %1 {mgmt.mgmt = #mgmt.mgmt<level = 1>} : i16
      %3 = arith.addi %2, %input1 {mgmt.mgmt = #mgmt.mgmt<level = 1>} : i16
      secret.yield %3 : i16
    } -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>})
    return %0 : !secret.secret<i16>
  }
}

-secret-insert-mgmt-bgv

Place BGV ciphertext management operations

This pass implements the following placement strategy:

For relinearize, after every homomorphic ciphertext-ciphertext multiplication, a mgmt.relinearize is placed after the operation. This is done to ensure that the ciphertext keeps linear.

For modulus switching, it is inserted right before a homomorphic multiplication, including ciphertext-plaintext ones. There is an option include-first controlling whether to switch modulus before the first multiplication.

User can check the FLEXIBLEAUTOEXT and FLEXIBLEAUTO mode in OpenFHE as a reference. To know more technical difference about them, user can refer to the paper “Revisiting homomorphic encryption schemes for finite firelds”.

Then, for level-mismatching binary operations like addition and subtraction, additional modulus switch is placed for the operand until it reaches the same level.

This is different from crosslevel operation handling in other implementations like using modulus switching and level drop together. The reason we only use modulus switching is for simplicity for now. Further optimization on this pass could implement such a strategy.

Before yield the final result, a modulus switching is placed if it is a result of multiplication or derived value of a multiplication.

Also, it annotates the mgmt.mgmt attribute for each operation, which includes the level and dimension information of a ciphertext. This information is subsequently used by the secret-to-bgv pass to properly lower to corresponding RNS Type.

Example

Command: heir-opt --secret-insert-mgmt-bgv tests/Transforms/secret_insert_mgmt_bgv/doctest.mlir

Input:

func.func @func(%arg0: !secret.secret<i16>, %arg1: !secret.secret<i16>) -> !secret.secret<i16> {
  %0 = secret.generic(%arg0: !secret.secret<i16>, %arg1: !secret.secret<i16>) {
  ^bb0(%arg2: i16, %arg3: i16):
    %1 = arith.muli %arg2, %arg3 : i16
    %2 = arith.addi %1, %arg3 : i16
    secret.yield %2 : i16
  } -> !secret.secret<i16>
  return %0 : !secret.secret<i16>
}

Output:

module attributes {scheme.bgv} {
  func.func @func(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}, %arg1: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}) -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>}) {
    %0 = secret.generic(%arg0: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}, %arg1: !secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 1>}) {
    ^body(%input0: i16, %input1: i16):
      %1 = arith.muli %input0, %input1 {mgmt.mgmt = #mgmt.mgmt<level = 1, dimension = 3>} : i16
      %2 = mgmt.relinearize %1 {mgmt.mgmt = #mgmt.mgmt<level = 1>} : i16
      %3 = mgmt.adjust_scale %input1 {id = 0 : i64, mgmt.mgmt = #mgmt.mgmt<level = 1>} : i16
      %4 = arith.addi %2, %3 {mgmt.mgmt = #mgmt.mgmt<level = 1>} : i16
      %5 = mgmt.modreduce %4 {mgmt.mgmt = #mgmt.mgmt<level = 0>} : i16
      secret.yield %5 : i16
    } -> (!secret.secret<i16> {mgmt.mgmt = #mgmt.mgmt<level = 0>})
    return %0 : !secret.secret<i16>
  }
}

Options

-after-mul                    : Modulus switching after each multiplication (default to false)
-before-mul-include-first-mul : Modulus switching before each multiplication, including the first multiplication (default to false)

-secret-insert-mgmt-ckks

Place CKKS ciphertext management operations

Check the description of secret-insert-mgmt-bgv. This pass implements similar strategy, where mgmt.modreduce stands for ckks.rescale here.

For bootstrap insertion policy, currently a greedy policy is used where when all levels are consumed then a bootstrap is inserted.

The max level available after bootstrap is controlled by the option bootstrap-waterline.

Number of bootstrap consumed level is not shown here, which is handled by further lowering. TODO(#1207): handle it here so parameter selection can depend on it. TODO(#1207): with this info we can encrypt at max level (with bootstrap consumed level).

Options

-after-mul                    : Modulus switching after each multiplication (default to false)
-before-mul-include-first-mul : Modulus switching before each multiplication, including the first multiplication (default to false)
-slot-number                  : Default number of slots use for ciphertext space.
-bootstrap-waterline          : Waterline for insert bootstrap op

-secret-merge-adjacent-generics

Merge two adjacent generics into a single generic

This pass merges two immediately sequential generics into a single generic. Useful as a sub-operation in some passes, and extracted into its own pass for testing purposes.

-secret-to-bgv

Lower secret to bgv dialect.

This pass lowers an IR with secret.generic blocks containing arithmetic operations to operations on ciphertexts with the BGV dialect.

The pass assumes that the secret.generic regions have been distributed through arithmetic operations so that only one ciphertext operation appears per generic block. It also requires that canonicalize was run so that non-secret values used are removed from the secret.generic’s block arguments.

The pass requires that all types are tensors of a uniform shape matching the dimension of the ciphertext space specified my poly-mod-degree.

Options

-poly-mod-degree : Default degree of the cyclotomic polynomial modulus to use for ciphertext space.

-secret-to-cggi

Lower secret to cggi dialect.

This pass lowers the secret dialect to cggi dialect.

-secret-to-ckks

Lower secret to ckks dialect.

This pass lowers an IR with secret.generic blocks containing arithmetic operations to operations on ciphertexts with the CKKS dialect.

The pass assumes that the secret.generic regions have been distributed through arithmetic operations so that only one ciphertext operation appears per generic block. It also requires that canonicalize was run so that non-secret values used are removed from the secret.generic’s block arguments.

The pass requires that all types are tensors of a uniform shape matching the dimension of the ciphertext space specified my poly-mod-degree.

Options

-poly-mod-degree : Default degree of the cyclotomic polynomial modulus to use for ciphertext space.

-secret-to-mod-arith

Lower secret to mod-arith dialect.

This pass lowers an IR with secret.generic blocks containing arithmetic operations to operations on plaintexts using the mod_arith dialect. This is primarily used in the plaintext lowering pipeline, where operations are performed directly against plaintexts.

The pass assumes that the secret.generic regions have been distributed through arithmetic operations so that only one ciphertext operation appears per generic block. It also requires that canonicalize was run so that non-secret values used are removed from the secret.generic’s block arguments.

Options

-modulus   : Modulus to use for the mod-arith dialect. If not specified, the pass will use the natural modulus for that integer type
-log-scale : Log base 2 of the scale for encoding floating points as ints.

-secretize

Adds secret argument attributes to entry function

Helper pass that adds a secret.secret attribute argument to each function argument. By default, the pass applies to all functions in the module. This may be overridden with the option -function=func_name to apply to a single function only.

Options

-function : function to add secret annotations to

-select-rewrite

Rewrites arith.select to a CMUX style expression

“This pass rewrites arith.select %c, %t, %f to %c * %t + (1 - %c) * %f. It supports all three variants of arith.select: scalar, shaped, and mixed types. In the latter case, it will broadcast/splat the scalar condition value to the required shape.”

-shape-inference

Infer shapes for shaped types

This pass infers the shapes of shaped types in a function, starting from function arguments annotated with a {shape.shape} attribute. Shape inference is only supported for operations that implement InferTypeOpInterface.

This is primarily intended to be used in conjunction with the Python frontend, which infers the rank, but not the length of each dimension, for tensor types.

-split-preprocessing

Splits a function into a preprocessing and a main part

This pass splits a function into a preprocessing and a main part. The preprocessing part is executed before the main function and its results are passed to the main function. This is used to allow packing of plaintexts to be done in advance of the main workload, and passed in as arguments. Only plaintexts of arith.constant ops are currently extracted for preprocessing.

Example

Command: heir-opt --split-preprocessing tests/Transforms/split_preprocessing/split_preprocessing.mlir

Input:

#vec_layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : (i0 - slot) mod 1024 = 0 and i0 >= 0 and 0 >= i0 and slot >= 0 and 1023 >= slot and ct = 0 }">

func.func @hoist_one_assign(%arg0: !secret.secret<tensor<4xi32>> {tensor_ext.layout = #vec_layout}) -> (!secret.secret<tensor<4xi32>> {tensor_ext.layout = #vec_layout}) {
  %c1 = arith.constant dense<1> : tensor<4xi32>
  %assign = tensor_ext.assign_layout %c1 {layout = #vec_layout} : tensor<4xi32>
  %0 = secret.generic(%arg0 : !secret.secret<tensor<4xi32>>) {
  ^body(%input0: tensor<4xi32>):
    %add = arith.addi %input0, %assign : tensor<4xi32>
    secret.yield %add : tensor<4xi32>
  } -> !secret.secret<tensor<4xi32>>
  return %0 : !secret.secret<tensor<4xi32>>
}

Output:

#layout = #tensor_ext.layout<"{ [i0] -> [ct, slot] : (i0 - slot) mod 1024 = 0 and i0 >= 0 and 0 >= i0 and slot >= 0 and 1023 >= slot and ct = 0 }">
module {
  func.func @hoist_one_assign__preprocessed(%arg0: !secret.secret<tensor<4xi32>> {tensor_ext.layout = #layout}, %arg1: tensor<4xi32> {tensor_ext.original_type = #tensor_ext.original_type<originalType = tensor<4xi32>, layout = #layout>}) -> (!secret.secret<tensor<4xi32>> {tensor_ext.layout = #layout}) {
    %0 = secret.generic(%arg0: !secret.secret<tensor<4xi32>>) {
    ^body(%input0: tensor<4xi32>):
      %1 = arith.addi %input0, %arg1 : tensor<4xi32>
      secret.yield %1 : tensor<4xi32>
    } -> !secret.secret<tensor<4xi32>>
    return %0 : !secret.secret<tensor<4xi32>>
  }
  func.func @hoist_one_assign(%arg0: !secret.secret<tensor<4xi32>> {tensor_ext.layout = #layout}) -> (!secret.secret<tensor<4xi32>> {tensor_ext.layout = #layout}) {
    %cst = arith.constant dense<1> : tensor<4xi32>
    %0 = tensor_ext.assign_layout %cst {layout = #layout} : tensor<4xi32>
    %1 = call @hoist_one_assign__preprocessed(%arg0, %0) : (!secret.secret<tensor<4xi32>>, tensor<4xi32>) -> !secret.secret<tensor<4xi32>>
    return %1 : !secret.secret<tensor<4xi32>>
  }
}

-straight-line-vectorize

A vectorizer for straight line programs.

This pass ignores control flow and only vectorizes straight-line programs within a given region.

Options

-dialect : Use this to restrict the dialect whose ops should be vectorized.

-tensor-ext-to-tensor

Lower tensor_ext to tensor dialect.

This pass lowers the tensor_ext dialect to the tensor dialect.

This pass is intended to be used for testing purpose where the secret arithmetic IR containing tensor_ext dialect is lowered to the IR containing tensor dialect, which could be further lowered to the LLVM dialect.

Example

Command: heir-opt --tensor-ext-to-tensor tests/Dialect/TensorExt/Conversions/tensor_ext_to_tensor/doctest.mlir

Input:

func.func @test_rotate(%0: tensor<16xi32>) -> tensor<16xi32> {
  %c5 = arith.constant 5 : i32
  %1 = tensor_ext.rotate %0, %c5 : tensor<16xi32>, i32
  return %1 : tensor<16xi32>
}

func.func @test_rotate_dynamic_multidim(%0: tensor<3x4x16xi32>, %shift: index) -> tensor<3x4x16xi32> {
  %1 = tensor_ext.rotate %0, %shift : tensor<3x4x16xi32>, index
  return %1 : tensor<3x4x16xi32>
}

Output:

module {
  func.func @test_rotate(%arg0: tensor<16xi32>) -> tensor<16xi32> {
    %c5_i32 = arith.constant 5 : i32
    %c16_i32 = arith.constant 16 : i32
    %extracted_slice = tensor.extract_slice %arg0[0] [5] [1] : tensor<16xi32> to tensor<5xi32>
    %extracted_slice_0 = tensor.extract_slice %arg0[5] [11] [1] : tensor<16xi32> to tensor<11xi32>
    %0 = tensor.empty() : tensor<16xi32>
    %inserted_slice = tensor.insert_slice %extracted_slice into %0[11] [5] [1] : tensor<5xi32> into tensor<16xi32>
    %inserted_slice_1 = tensor.insert_slice %extracted_slice_0 into %inserted_slice[0] [11] [1] : tensor<11xi32> into tensor<16xi32>
    return %inserted_slice_1 : tensor<16xi32>
  }
  func.func @test_rotate_dynamic_multidim(%arg0: tensor<3x4x16xi32>, %arg1: index) -> tensor<3x4x16xi32> {
    %c16 = arith.constant 16 : index
    %0 = arith.remsi %arg1, %c16 : index
    %1 = arith.addi %0, %c16 : index
    %2 = arith.remsi %1, %c16 : index
    %3 = arith.subi %c16, %2 : index
    %extracted_slice = tensor.extract_slice %arg0[0, 0, 0] [3, 4, %2] [1, 1, 1] : tensor<3x4x16xi32> to tensor<3x4x?xi32>
    %extracted_slice_0 = tensor.extract_slice %arg0[0, 0, %2] [3, 4, %3] [1, 1, 1] : tensor<3x4x16xi32> to tensor<3x4x?xi32>
    %4 = tensor.empty() : tensor<3x4x16xi32>
    %inserted_slice = tensor.insert_slice %extracted_slice into %4[0, 0, %3] [3, 4, %2] [1, 1, 1] : tensor<3x4x?xi32> into tensor<3x4x16xi32>
    %inserted_slice_1 = tensor.insert_slice %extracted_slice_0 into %inserted_slice[0, 0, 0] [3, 4, %3] [1, 1, 1] : tensor<3x4x?xi32> into tensor<3x4x16xi32>
    return %inserted_slice_1 : tensor<3x4x16xi32>
  }
}

-tensor-linalg-to-affine-loops

A port of convert-linalg-to-affine-loops for loops with tensor semantics

This pass primarily exists to support the conversion of linalg.generic operations that implement tensor_ext.assign_layout ops.

-unroll-and-forward

Loop unrolls and forwards stores to loads.

This pass processes the first function in a given module, and, starting from the first loop, iteratively does the following:

  1. Fully unroll the loop.
  2. Scan for load ops. For each load op with a statically-inferrable access index:
  3. Backtrack to the original memref alloc
  4. Find all store ops at the corresponding index (possibly transitively through renames/subviews of the underlying alloc).
  5. Find the last store that occurs and forward it to the load.
  6. If the original memref is an input memref, then forward through any renames to make the target load load directly from the argument memref (instead of any subviews, say)
  7. Apply the same logic to any remaining loads not inside any for loop.

This pass requires that tensors are lowered to memref, and only supports affine loops with affine.load/store ops.

Memrefs that result from memref.get_global ops are excluded from forwarding, even if they are loaded with a static index, and are instead handled by memref-global-replace, which should be run after this pass.

-validate-noise

Validate the HE circuit against a given noise model

This pass validates the noise of the HE circuit against a given noise model.

The pass expects the scheme parameters to be annotated in the IR. Usually this is done by the generate-param-<scheme> passes.

For available noise models, see generate-param-<scheme> passes.

The result should be observed using –debug-only=ValidateNoise.

Example

# with commandline --debug-only=ValidateNoise
Noise Bound: 29.27 Budget: 149.73 Total: 179.00 for value: <block argument> of type 'tensor<8xi16>' at index: 0
Noise Bound: 29.27 Budget: 149.73 Total: 179.00 for value: <block argument> of type 'tensor<8xi16>' at index: 1

Options

-model                : Noise model to validate against.
-annotate-noise-bound : Annotate the noise bound to the IR.

-wrap-generic

Wraps regions using secret args in secret.generic bodies

This pass converts functions (func.func) with {secret.secret} annotated arguments to use !secret.secret<...> types and wraps the function body in a secret.generic region. The output type is also converted to !secret.secret<...>.

Example

Command: heir-opt --wrap-generic tests/Transforms/wrap_generic/doctest.mlir

Input:

func.func @main(%arg0: i32 {secret.secret}) -> i32 {
  %0 = arith.constant 100 : i32
  %1 = arith.addi %0, %arg0 : i32
  return %1 : i32
}

Output:

module {
  func.func @main(%arg0: !secret.secret<i32>) -> !secret.secret<i32> {
    %0 = secret.generic(%arg0: !secret.secret<i32>) {
    ^body(%input0: i32):
      %c100_i32 = arith.constant 100 : i32
      %1 = arith.addi %c100_i32, %input0 : i32
      secret.yield %1 : i32
    } -> !secret.secret<i32>
    return %0 : !secret.secret<i32>
  }
}

-yosys-optimizer

Invoke Yosys to perform circuit optimization.

This pass invokes Yosys to convert an arithmetic circuit to an optimized boolean circuit that uses the arith and comb dialects.

Note that booleanization changes the function signature: multi-bit integers are transformed to a tensor of booleans, for example, an i8 is converted to tensor<8xi1>.

The optimizer will be applied to each secret.generic op containing arithmetic ops that can be optimized.

Optional parameters:

  • abc-fast: Run the abc optimizer in “fast” mode, getting faster compile time at the expense of a possibly larger output circuit.
  • unroll-factor: Before optimizing the circuit, unroll loops by a given factor. If unset, this pass will not unroll any loops.
  • print-stats: Prints statistics about the optimized circuits.
  • mode={Boolean,LUT}: Map gates to boolean gates or lookup table gates.
  • use-submodules: Extract the body of a generic op into submodules. Useful for large programs with generics that can be isolated. This should not be used when distributing generics through loops to avoid index arguments in the function body.

Statistics

total circuit size : The total circuit size for all optimized circuits, after optimization is done.